一种运动部分解耦的2R2T并联机构运动学与性能分析
2019-02-15李秦川张克涛
叶 伟 李秦川 张克涛
(1.浙江理工大学机械与自动控制学院, 杭州 310018; 2.伦敦玛丽女王大学工程与材料学院, 伦敦 E1 4NS)
0 引言
相比于六自由度并联机构,少自由度并联机构具有工作空间大、制造成本低、控制简单等优点,因此得到了广泛的研究[1-8]。能输出两转动两移动(Two rotations and two translations, 2R2T)运动的并联机构可用于农业振动筛[9]、外科手术[10]或者配合移动工作台形成五轴机床[11]。学者们提出了各种方法进行2R2T并联机构的构型综合,包括约束综合方法[12],构型演变和李群理论的方法[13-14],基于GF集理论的方法[15]和运动等效链的方法[16]。
大多数情况下,并联机构的运动具有耦合性,即每个自由度方向的运动都需要所有的主动关节配合驱动,这使得机构运动学模型复杂、难于控制。为解决这个问题,具有运动解耦特点的并联机构被广泛研究。GOGU[17-18]采用线性变换的方法研究了多类运动解耦并联机构的综合。SHARIFZADEH等[19]研究了运动解耦三平动并联机构的动力学建模。ZENG等[20]采用螺旋理论的方法,开展了运动解耦并联机构的研究。张彦斌等[21]采用螺旋理论,提出了运动解耦2R2T并联机构结构综合的新方法。沈惠平等[22]提出了一类新型位置-姿态运动解耦的并联机构。
目前,运动解耦的2R2T并联机构实用构型仍然较少,关于这类机构的运动学及性能分析鲜有报道。本文提出一种运动部分解耦的新型2R2T并联机构,采用李群理论分析其自由度,并开展运动学性能相关分析,为其实际应用提供理论基础。
1 机构简介与自由度分析
如图1、2所示,本文提出并联机构的动平台通过4条分支与基座相连。其中,分支2是PRU链(P为移动副,R为转动副,U为虎克铰),分支3是PSS链(S为球副),分支1、4可视作共用末端虎克铰的两个PRU链。机构中所有移动副轴线平行。分支1、2、4处于同一平面,其中所有转动副轴线平行于虎克铰的第一转动轴线,且垂直于移动副轴线。机构中两个虎克铰与动平台连接的转动轴线重合。
记分支1、2、4中转动副中心点为A1、A2、A4,虎克铰中心点为B1、B2,记分支3内与移动副相邻的球副中心点为A3,与动平台相邻的球副中心点为B3。点A1、A2、A3在水平面的投影形成等腰三角形C1C2C3,其中lC1C3=lC2C3,C1C2长度为2a,C3到线段C1C2的垂直距离为a。动平台B1B2B3也为等腰三角形,lB1B3=lB2B3,B1B2长度为b,B3到线段B1B2的垂直距离为b/2。在基座水平面上建立定坐标系oxyz,其中原点o位于C1C2中点,x轴指向点C2,y轴指向点C3,z轴垂直于水平面向上。在动平台上建立动坐标系puvw,其中原点p与B1点重合,u轴指向点B2,v轴位于动平台平面且垂直于B1B2,w轴由右手定则决定。

图1 并联机构简图Fig.1 Diagram of parallel manipulator

图2 并联机构三维模型Fig.2 3D model of parallel manipulator
采用李群理论[2]分析机构的自由度,注意到分支1和分支4在B1点共用虎克铰,杆A1B1和A4B1通过复合转动副连接到虎克铰的第一转轴,因此分支1和分支4形成一个局部的PRR-PRR平面闭环。将分支1和分支4整体考虑,其到动平台的运动可表示为
L14=({T(z)}{R(A1,y)}{R(B1,y)}∩
{T(z)}{R(A4,y)}{R(B1,y)})∪{R(B1,u)}=
({G(y)}∩{G(y)})∪{R(B1,u)}=
{G(y)}{R(B1,u)}
(1)
式中L14——分支1和分支4整体到动平台的运动集
{T(z)}——沿z轴方向的移动运动群
{R(A1,y)}——轴线过点A1且平行于向量y的转动运动群
{G(y)}——垂直于向量y的平面运动群
其余符号类同。
同理,分支2的运动集L2可表示为
L2={T(z)}{R(A2,y)}{R(B2,y)}{R(B2,u)}=
{G(y)}{R(B2,u)}
(2)
因点B1、B2同在u轴上,{R(B1,u)}={R(B2,u)},故
L2={G(y)}{R(B2,u)}={G(y)}{R(B1,u)}
(3)
由于分支3具有6自由度,其运动集L3是六维李群,可表示为
L3={D}
(4)
根据李群理论,动平台的运动是分支运动集的交集,可得
{M}=L14∩L2∩L3=
{G(y)}{R(B1,u)}∩{G(y)}{R(B1,u)}∩{D}=
{G(y)}{R(B1,u)}
(5)
式中 {M}——动平台运动集式(5)表明,该并联机构具有4个自由度,分别是垂直于y轴的2个移动自由度、轴线平行于y轴的转动自由度和绕u轴的转动自由度。由于李群描述的是连续运动,该机构的4个自由度也是连续的。
在刚化4个移动副(即将对应的运动群移除)之后,仍采用上面的分析步骤可以发现机构的自由度为零,这说明了4个移动副可作为驱动关节完全控制动平台的运动。
该并联机构可应用于五轴机床或运动模拟器的开发。图3给出了一种五轴机床案例,将主轴头固定在动平台上,在基座上配置一个移动工作台,则刀具与工件可形成五自由度相对运动,可实现任意曲面的五轴加工。该机床的一个显著优点是驱动都是与机架相连的移动副,驱动电机无需跟随机器运动,可获得很好的动态特性。

图3 五轴机床Fig.3 Five axis machine1.主轴头 2.工件 3.移动工作台
2 位置分析
位置分析目的在于建立动平台位姿输出参数与驱动关节输入参数间的关系。本文提出的机构中,驱动关节为各分支中的移动副。由于点o和点p始终在xoz平面内,动坐标系可视为将定坐标系沿向量p=(x,0,z)T平移,再绕y轴转动角度α,最后绕x轴转动角度β得来。动平台的位姿参数可由两个位置参数x、z和两个姿态参数α、β表示。
显然,当分支1和分支4中移动副位置参数给定后,点B1位置就已确定,即输出参数x和z的值完全由分支1和分支4的输入参数决定。因此,该机构具有运动部分解耦的特点。
令di(i=1, 2, 3, 4)表示分支i中移动副的位移。根据前述几何关系,点Ai在定坐标系中的位置矢量为
(6)
式中d——C1C4的长度
点Bi在动坐标系下的位置矢量为
(7)
式中,上标p表示参考坐标系是动坐标系。
点Bi在定坐标系中的位置矢量为
(8)
其中

(9)
式中R——姿态变换矩阵
将式(7)代入式(8),可得
(10)
观察分支结构,可得约束方程
(11)
式中l——连杆AiBi长度
将式(6)、(10)代入式(11),可得
f1:(x+a)2+(z+d1)2=l2
(12)
f2:(x+bcosα-a)2+(z-bsinα+d2)2=l2
(13)
(14)
f4:(x+a)2+(z-d4+d)2=l2
(15)
位置逆解是在给定动平台输出参数x、z、α、β的条件下,求解驱动关节输入参数di(i=1, 2, 3, 4)。根据式(12)~(15),可得位置逆解的表达式为
(16)
式中“±”表明每条分支存在两种反解情况,对应图1中装配方式,式中均取“-”号。
位置正解是给定各驱动输入参数di,求解动平台输出参数x、z、α、β,可按以下步骤进行:
(1)首先,令式(15)减去式(12),可得到z的解析表达式为
(17)
(2)在z确定之后,通过式(12)可得
(18)
由式(18)可知,在给定d1和d4后,x有两种情况。在图1所示的装配条件下,“±”应取正号。为表达简单起见,z的具体表达式并未代入式(18)中。
可知,x和z的表达式中仅含输入变量d1和d4后,证明了输出参数x和z的值完全由分支1和分支4的输入参数决定。
(3)在得到x和z的表达式后,可通过式(13)解出α。将式(13)展开,可得

(19)
(20)
其中

通过式(20)可得
(21)
则α表达式为
α=2arctant1
(22)
分析可知,α仅和输入参数d1、d2、d4有关。在x和z确定后,对应某一给定的d2,α有两种可能,分别对应两种不同的装配方式。

β=2arctant2
(23)
可知,β和所有的4个输入参数都有关。在x、z和α确定后,对应某一给定的d3,β同样有两种可能。因此,在给定的一组输入参数d1、d2、d3和d4后,动平台的位置正解共有8种可能情况,可结合机构的初始装配条件确定正确的位置正解。通过以上分析发现,该机构的位置正解可得到解析的表达式,是一个显著的优点。
需要注意的是,在机构的实际应用中,操作端如刀具等可能不便于安装在本节所建立的动坐标系原点p(B1)处,但可将刀具安装在点B1和B2连线上,这样刀具在y方向上位置仍保持为0。如果刀具安装在动平台上的一般位置,则刀具在y方向上将会产生伴随运动,与输出参数x、z、α、β线性相关。无论刀具安装于何位置,由于动平台参数x、z、α、β具有解析的表达式,刀具的位置和姿态参数也都可方便地得到。
为验证位置正反解模型的正确性,给定机构参数a=160 mm,b=140 mm,杆AiBi长度l=200 mm,d=500 mm。给定一组输入参数d1=144.64 mm,d2=122.08 mm,d3=105.16 mm,d4=144.64 mm。根据上述位置正解步骤,可得动平台输出参数如表1所示。
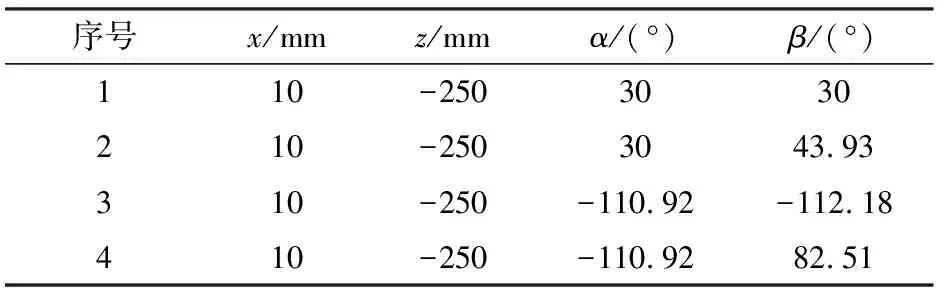
表1 位置正解数据Tab.1 Direct position results
表1仅列出了正解中的4组实数解。取正解的第1组数据,代入式(16)中,可得到4个输入参数的16组逆解结果。其中存在一组数据为d1=144.64 mm,d2=122.08 mm,d3=105.16 mm,d4=144.64 mm,与正解数值计算中给定的4个输入值一致,验证了位置正反解的正确性。
3 速度与奇异分析
并联机构的奇异位形会带来机构失控等严重后果,应予以分析。速度方程是奇异分析的基础。对方程(12)~(15)求导,可得机构的速度方程,整理得
(24)
其中

图5 正解奇异Fig.5 Direct kinematic singularity
式(24)进一步证明了机构在x和z方向的移动自由度仅由分支1和分支4控制,机构具有运动部分解耦的特点。
根据文献[23]中的分类方法,可按照雅可比矩阵行列式值的情况,将奇异分为逆解奇异、正解奇异和混合奇异。
(1)逆解奇异
当det(JA)=0且det(JB)≠0时,机构发生逆解奇异。分析可知,仅当某条分支中杆AiBi垂直于所在分支中移动副轴线时,满足逆解奇异条件。机构的一种逆解奇异位形如图4所示。此时,动平台的自由度瞬时减少。

图4 逆解奇异Fig.4 Inverse kinematic singularity
(2)正解奇异
当det(JB)=0且det(JA)≠0时,机构发生正解奇异。分析可知,存在两种正解奇异情况。
情况1:点A2、B2、B1共线。此时,动平台绕y轴方向的转动不受控制。图5a给出了一种对应的正解奇异位形。
情况2:线A3B3与线B1B2相交。此时,机构绕u轴的转动不受控制。图5c给出了一种对应的正解奇异位形。
在位置分析部分给定机构参数情况下,令z=-250 mm,根据det(JB)=0,可绘制工作空间内的正解奇异曲面,其中,正解奇异情况1、2分别对应两个空间曲面,如图5b所示。
(3)组合奇异
当det(JA)=0且det(JB)=0时,机构发生混合奇异。图6给出了其中一种情况。
图6 组合奇异Fig.6 Combined singularity
4 工作空间
工作空间衡量的是机构末端在各自由度方向的运动能力。由于内部多分支的约束,并联机构工作空间通常较小。本文机构的工作空间受关节运动范围限制,机构尺度参数于正解奇异部分给定。限定移动副行程为0 mm≤di≤250 mm,球副转动范围限制在50°的锥体内。由于机构驱动关节均为沿z轴方向的移动副,令z=-250 mm,可得机构的三维工作空间如图7所示。
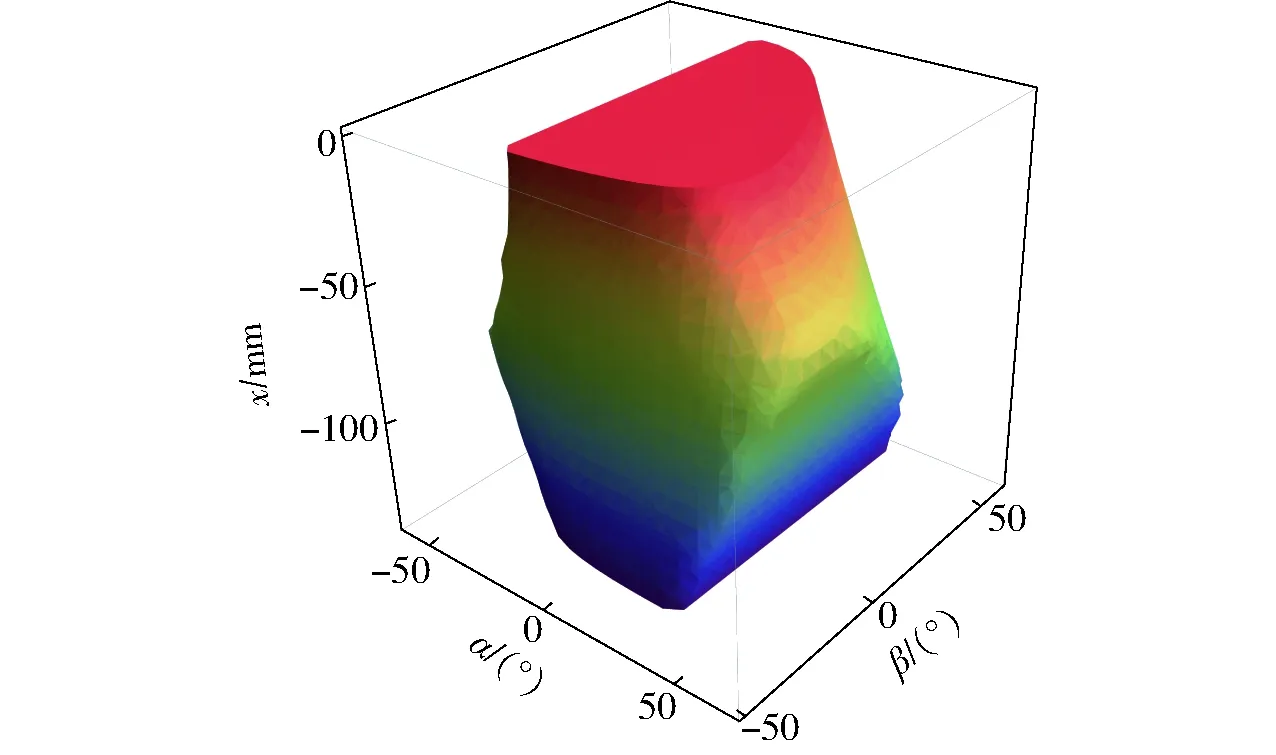
图7 工作空间Fig.7 Workspace

图8 机构二维工作空间与奇异曲线Fig.8 Two-dimensional workspace and singular curves
需要注意的是,正解奇异可能存在工作空间内部,将工作空间分割成若干部分。为方便观察,令x分别取-140、-70、0 mm,绘制α和β参数的二维工作空间和奇异曲线,如图8所示。可以发现,机构的正解奇异分布在工作空间边缘部分,几乎不影响机构的转动能力;机构的无奇异转动空间很大,中间位置(图8b)两个方向的转角范围分别可达-44°~60°和-35°~52°。
5 性能分析
并联机构的运动学性能分析是为了研究机构在工作空间内是否具有良好的操作性能,是机构尺度优化设计的基础。并联机构的运动学性能主要包括基于雅可比矩阵的条件数指标[24]和基于螺旋理论的运动/力传递指标[25-26]。由于本文机构具有移动和转动混合自由度,使用条件数指标存在量纲不统一、物理意义不清晰的问题[27],因此,采用运动/力传递指标对机构进行性能分析。
5.1 局部传递指标
运动/力传递方法中分别定义输入传递指标、输出传递指标和局部传递指标为
(25)
(26)
Γ=min{λi,ηi} (i=1,2,…,n)
(27)
式中λi——分支i的输入传递指标
ηi——分支i的输出传递指标
Γ——局部传递指标
$Ai——分支i的输入运动螺旋
$Oi——分支i的输出运动螺旋
$Ti——分支i的传递力螺旋
λi、ηi和Γ是与坐标系无关的无量纲指标,取值在0~1之间,Γ越趋近1,表明机构的运动/力传递性能越好,而Γ越趋近0,表明机构越靠近奇异位形。
在坐标系oxyz中,令ria(i=1, 2, 3, 4)和rib(i=1, 2, 3)分别表示Ai点和Bi点的位置矢量,分支1的运动螺旋为
(28)
式中 $11——移动副运动螺旋
$12——转动副运动螺旋
$13——虎克铰第1转动运动螺旋
$14——虎克铰第2转动运动螺旋
O——零向量
对式(28)求反螺旋,可得分支1的约束螺旋为
(29)
分支1输入运动螺旋$A1=$11,传递力螺旋$Ti与分支内所有被动螺旋互易积为零,即
$T1∘$1j=0 (j=2, 3, 4)
(30)
可求得分支1传递力螺旋为
$T1=(rA1B1;r1a×rA1B1)
(31)
式中rA1B1——沿A1B1方向的单位向量
$T1——沿杆A1B1方向的传递力螺旋
同理,可得分支2、3、4的传递力螺旋分别为
$T2=(rA2B2;r2a×rA2B2)
(32)
$T3=(rA3B3;r3a×rA3B3)
(33)
$T4=(rA4B1;r4a×rA4B1)
(34)
为求分支1传递力螺旋$T1对应的输出运动螺旋,可将分支2、3、4中传递力螺旋视为约束螺旋,与机构约束螺旋系组合形成一个秩为5的螺旋系。对该螺旋系求反螺旋,则可得到分支1的输出运动螺旋$O1。类似地,可以求得分支2、3、4的输出运动螺旋$O2、$O3和$O4。
将求得的输入运动螺旋、传递力螺旋和输出运动螺旋代入式(25)~(27)中,可得机构的局部传递指标。图9给出的是在前述机构尺度参数下,z=-250 mm,x=-70 mm时姿态工作空间中心区域的局部传递指标分布。对比图8b和图9可得,机构的性能分布趋势与奇异曲线吻合。越靠近奇异位形,机构的性能越差。这也证明了性能分析的正确性。

图9 局部传递指标分布图 (a=160 mm,l=200 mm)Fig.9 Distribution diagram of local transmission index (a=160 mm,l=200 mm)
5.2 全域传递指标
局部传递指标可用于机构的尺度优化设计,定义工作空间内局部传递指标大于0.7的区域为优质传递空间,优质传递空间与整体工作空间的比值为全域传递指标
(35)
式中W——机构的整体工作空间
SG——优质传递空间的面积
S——整体工作空间的面积
σ——全域传递指标
显然σ取值于0到1之间,σ越大,表明机构优质传递空间越大,机构的性能越好。
以基座尺寸a和连杆长度l为设计变量,计算不同变量对应的σ,并绘制成平面图(图10),则可发现σ随机构尺度参数的变化规律,从而可以选取性能更优的机构尺度参数。

图10 全域传递指标变化图Fig.10 Variation of global transmission index
图9对应机构尺度参数a=160 mm,l=200 mm,对应图10中点1,此时,σ=0.47。可在点1左上方取点2,对应a=150 mm,l=210 mm,σ=0.54。显然,点2尺度参数对应的机构性能更优,绘制该参数下的局部传递指标分布图如图11所示。可以发现,局部传递指标大于0.7的部分(白线所围区域)相较于图9得到了扩大,机构性能得到了优化。
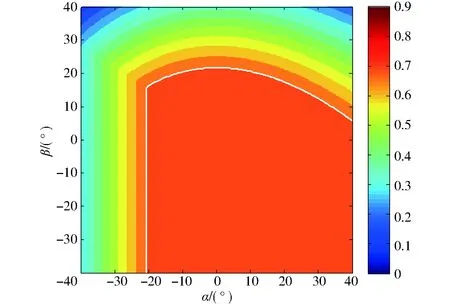
图11 局部传递指标分布图 (a=150 mm,l=210 mm)Fig.11 Distribution diagram of local transmission index (a=150 mm,l=210 mm)
6 结论
(1)提出了一种新型并联机构,能输出两个转动和两个移动自由度,可由固定移动副驱动。该机构位置参数仅由两条分支决定,具有运动部分解耦的特点,可用于五轴机床或运动模拟器的本体。
(2)该机构存在逆解奇异、正解奇异和组合奇异。正解奇异位于工作空间的边缘。机构的无奇异转动空间很大,中间位置两个方向的转角范围分别可达-44°~60°和-35°~52°。
(3)机构的运动/力传递性能分布反映了距离奇异位形的远近。机构在工作空间内具有良好的性能,且可通过尺度设计进一步进行优化。
