基于彭曼公式日均值时序分析的中国蒸发能力动态成因

白 桦 鲁向晖 杨筱筱 高 鹏 桂发亮 穆兴民

(1.中国科学院水利部水土保持研究所黄土高原土壤侵蚀与旱地农业国家重点实验室， 陕西杨凌 712100； 2.中国科学院大学， 北京 100049； 3.南昌工程学院江西省水文水资源与水环境重点实验室， 南昌 330099； 4.江西省水文局， 南昌 330002)

0 引言

蒸发能力是特定气候条件下地表充分供水时的蒸发量，广泛用于陆气耦合的靶向研究。蒸发能力是涵盖性术语，包含潜在蒸发量(Potential evapotranspiration，ETp)和参考作物蒸发蒸腾量。综合能量平衡和质量传输理论，彭曼公式所求潜在蒸发量最初用于估算开阔水面蒸发量[1]，后结合彭曼[1-2]、BOUCHET[3]和BUDYKO[4-6]假设，估算区域和流域实际蒸发量。彭曼-蒙特斯公式引入空气动力学和冠层阻力系数[7]，用于参考作物蒸发蒸腾量的估算和作物需水量的预报预测[8-9]。对比可知，潜在蒸发量更被广泛地用于中大空间尺度区域和流域蒸发量及伴生水能通量的衡量。

潜在蒸发量变化成因定量分析多借助彭曼公式全微分求积方程[10]，应用于澳大利亚和江西等地[10-11]。彭曼公式是自变量温度、风速、净辐射量(Net radiation，Rn)和相对湿度的四元非线性方程。在四维空间上，彭曼公式全微分的曲线积分值与路径无关[12]。但各自变量对曲线积分值的贡献率却严重依存于积分路径。究其原因，该贡献率是潜在蒸发量对自变量偏导数和自变量对时间导数的函数。潜在蒸发量对自变量偏导数随积分路径中系统状态变量而改变。自变量对时间导数常以两者线性回归方程斜率代替，概化误差较大。积分路径时间尺度越小，路径越接近气候的实际变化过程，自变量对曲线积分的贡献率越真实，成因分析越可靠。

本文分析中国年潜在蒸发量时空变化，构建彭曼公式全微分日求积方法，计算年均日潜在蒸发量变化的气象要素累积贡献率，甄别驱动因子和成因，为我国水资源和水灾害演变规律和成因分析及灾害预测预报提供科学依据。

1 数据与方法

1.1 数据

所用数据来源于国家气象科学数据共享服务平台(http:∥data.cma.cn/site/index.html)中国地面气候资料日值数据集(V3.0)，包含中国819个基础气象站1961—2015年逐日平均温度(T)、相对湿度(Hu)、风速(u2)、日照时数等气象资料和各站经纬度、高程等地理信息数据。在819个基础气象站中有114个站具备相对完整的地表辐射和日照时数资料(缺测率小于等于20%)，将该114个基础气象站命名为辐射站，用于估算地表辐射经验模型Ångström-Prescott模型(简称为A-P模型)参数[13-14]，见图1。所有站点数据均进行了严格的质量控制，但仍存在部分数据缺测现象。在数据处理和分析过程中遇到数据缺测现象时，直接剔除该日所有数据。

图1 中国气象站和辐射站空间分布Fig.1 Spatial distribution of meteorological and radiation stations

1.2 方法

1.2.1中国年蒸发能力动态分析方法

采用中国114个辐射站1961—2015年实测逐日地表辐射和日照时数数据，假设两者之间关系可由A-P模型描述，采用最小二乘法[15]、均方根误差RMSE和Nash-Sutcliffe效率系数[16]分别对A-P模型参数、模型模拟地表辐射量均方根误差和模型模拟效果进行分析。若A-P模型模拟效果较好，则采用Lilliefors检验(显著性水平为0.05)[17-18]，验证辐射站A-P模型参数是否服从正态分布。对比参数经验和正态分布理论概率分布曲线，进一步验证。综合检验结果，若模型参数服从正态分布，则基于ArcGIS平台，采用克里格插值法[19]，获取气象站A-P模型参数和逐日地表辐射量模拟值；若模型参数不服从正态分布，则基于ArcGIS平台，采用反距离权重法[20]，获取气象站A-P模型参数和逐日地表辐射量模拟值。计算各气象站逐日实测最低和最高气温的平均值，即为逐日平均气温；各站距地2 m高处风速由实测10 m高风速转换而来[7]。结合各气象站逐日气温、相对湿度、风速和地表净辐射等数据，采用彭曼潜在蒸发量公式[1]估算各站逐日、逐年和多年平均潜在蒸发量。

类似A-P模型参数正态分布验证流程，检验各站多年平均潜在蒸发量是否服从正态分布。基于ArcGIS平台，采用克里格或反距离权重插值方法，绘制中国多年平均潜在蒸发量等值线图，揭示其空间分布规律。选取各站逐年潜在蒸发量，计算各站年潜在蒸发量相对时间的决定系数(R2)，对比决定系数临界值(显著性水平为0.05)。若决定系数大于其临界值，采用线性回归方法计算年潜在蒸发量倾向率[21]；若决定系数小于其临界值，将年潜在蒸发量倾向率赋值为0，绘制年潜在蒸发量倾向率等值线图，揭示中国年潜在蒸发量趋势空间分布。针对年潜在蒸发量趋势显著的气象站，采用Pettitt和Mann-Kendall突变点检验法检验各站年潜在蒸发量突变点(显著性水平为0.05)[22-24]。以泰森多边形法确定各站突变年份代表区域[19]，采用众数滤波、焦点统计方法揭示突变年份空间分布特征[25-26]；同时统计各站突变点的代际比例，表征突变年份时间分布。

1.2.2气象站日蒸发能力一阶差分值模拟方法

选取年潜在蒸发量趋势显著且存在突变点的气象站，基于各站1961—2015年逐日潜在蒸发量，采用向前差分方法，计算各站逐日潜在蒸发量、地表辐射量、气温、风速和相对湿度的向前一阶差分值，即实测值。利用彭曼公式全微分日尺度求积方程

ΔETp=ΔETpr+ΔETpa

(1)

其中

式中ETpr、ETpa——逐日彭曼潜在蒸发量辐射项、空气动力项,mm/d

ΔETp——逐日彭曼潜在蒸发量向前一阶差分值，mm/d

ΔETpr——逐日彭曼潜在蒸发量辐射项向前一阶差分值，mm/d

ΔETpa——逐日彭曼潜在蒸发量空气动力项向前一阶差分值，mm/d

ΔETpr,T——温度引起的辐射项变化量，mm/d

ΔETpr,Rn——地表净辐射引起的辐射项变化量，mm/d

ΔETpa,T——温度引起的逐日空气动力项变化量，mm/d

ΔETpa,Hu——相对湿度引起的逐日空气动力项变化量，mm/d

ΔETpa,u2——风速引起的逐日空气动力项变化量，mm/d

es、ea——饱和、实际水汽压，kPa

Δ——饱和水汽压温度曲线斜率，kPa/℃

积分下限为系统原始状态变量值。

将逐日潜在蒸发量一阶差分值分解为部分差分值[10]

(2)

式中 ΔETp,T——温度引起的潜在蒸发量变化量，mm/d

γ——干湿表常数，kPa/℃

λ——蒸发潜热，MJ/kg

D——参考高度的空气饱和水汽压差，kPa

ΔT——日均温度一阶差分值，℃

(3)

式中 ΔETp,Hu——相对湿度引起的潜在蒸发量变化量，mm/d

ΔHu——日均相对湿度一阶差分值，%

(4)

式中 ΔETp,Rn——净辐射量引起的潜在蒸发量变化量，mm/d

ΔRn——日地表净辐射量一阶差分值，MJ/(m2·d)

(5)

式中 ΔETp,u2——风速引起的潜在蒸发量变化量，mm/d

Δu2——日均风速一阶差分值，m/s

各气象要素相应部分差分值是该要素对日潜在蒸发量一阶差分值的贡献量[10]。部分差分值求和，即日潜在蒸发量一阶差分模拟值。采用线性回归方程[21]、决定系数及其临界值、t检验值及其临界值[27]检验各站日潜在蒸发量一阶差分值的模拟效果。

1.2.3中国年均日蒸发能力变化归因方法

(1)年均日蒸发能力变化及成因定性分析

依据各气象站年潜在蒸发量突变年份，将各站研究时段进行时段划分。计算各站相邻时段相应日潜在蒸发量平均值。突变点之后与之前时段均值的差值即为各站年均日潜在蒸发量差分值。

(6)

n——突变年份相应日序值

(7)

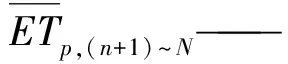
N——日潜在蒸发量样本容量

(8)

借助气象要素对逐日潜在蒸发量一阶差分值的贡献量，将年均日潜在蒸发量差分值分解为各要素累积贡献量。

(9)

其中

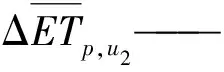
ΔETp,T,i——温度引起的第i日潜在蒸发量变化量，mm/d

ΔETp,T,n+j——温度引起的第n+j日潜在蒸发量变化量，mm/d

ΔETp,u2,i——风速引起的第i日潜在蒸发量变化量，mm/d

ΔETp,u2,n+j——风速引起的第n+j日潜在蒸发量变化量，mm/d

ΔETp,Rn,i——地表净辐射量引起的第i日潜在蒸发量变化量，mm/d

ΔETp,Rn,n+j——地表净辐射量引起的第n+j日潜在蒸发量变化量，mm/d

ΔETp,Hu,i——相对湿度引起的第i日潜在蒸发量变化量，mm/d

ΔETp,Hu,n+j——相对湿度引起的第n+j日潜在蒸发量变化量，mm/d

对比年均日潜在蒸发量差分值及气象要素累积贡献量时序演变过程，定性揭示蒸发能力变化及成因。

(2)年均日蒸发能力变化成因定量分析

计算各站累积贡献量与年均日潜在蒸发量差分值的比值，即为累积贡献率。截取气象站最大累积贡献率相应气象要素作为该站主驱动要素。以泰森多边形法确定各站主驱动要素代表区域[19]，采用众数滤波、焦点统计方法分析各站主驱动要素的空间分布特征[25-26]，并进行区划。在各分区内，计算各气象要素累积贡献率均值。选取均值大于100的气象要素作为分区主驱动要素。综合分析潜在蒸发量趋势和驱动要素的空间分布特征，定量揭示年均日蒸发能力变化成因。

2 结果与分析

2.1 中国年蒸发能力动态

2.1.1气象站日净辐射量和蒸发能力估算

基于中国114个辐射站1961—2015年实测逐日地表辐射和日照时数数据，假设两者间关系可由A-P模型描述，采用最小二乘法和均方根误差RMSE、Nash-Sutcliffe效率系数分别对A-P模型参数和模拟效果进行分析(图2)。结果表明，辐射站A-P模型参数a在0.47～0.69间变化，平均值为0.55，最大和最小值分别出现在甘肃武威站和新疆阿克苏站。模型参数b在0.13～0.29间变化，平均值为0.19，最大和最小值分别出现在新疆库车站和浙江慈溪站。多年平均实测地表辐射量在8.75～21.12 MJ/(m2·d)间，平均值为14.28 MJ/(m2·d)，其模拟值在8.68～21.25 MJ/(m2·d)间变化，平均值为14.30 MJ/(m2·d)，实测和模拟最大和最小值均分别出现在广西北海站和内蒙古锡林浩特站。模型模拟和实测地表辐射量间RMSE在1.61～4.31 MJ/(m2·d)间变化，平均值2.48 MJ/(m2·d)，表明模型模拟值相对实测值偏离程度较小，模拟精度较高。Nash-Sutcliffe效率系数在0.59～0.96之间变化，平均值为0.88，表明A-P模型模拟可信度

图2 Ångström-Prescott模型参数和模拟效果Fig.2 Parameters and simulation effect of Ångström-Prescott model

较高。借助Matlab软件，采用Lilliefors方法(显著性水平为0.05)检验辐射站A-P模型参数。结果表明：模型参数a、b检验值均为0，尺度参数分别为0.5和0.1，均服从正态分布。借助ArcGIS平台，采用克里格插值方法获取各气象站A-P模型参数和逐日地表辐射量。结合气象站逐日气温、相对湿度、风速等数据，采用彭曼公式估算各站逐日、逐年、多年平均潜在蒸发量。

2.1.2中国年蒸发能力空间分布格局

采用Lilliefors方法检验各站多年平均潜在蒸发量(显著性水平为0.05)。结果表明Lilliefors检验值为1，尺度参数为0.001，各站多年平均潜在蒸发量不服从正态分布。绘制各气象站多年平均潜在蒸发量经验概率和正态分布理论频率曲线(图3a)，验证各站多年平均潜在蒸发量是否服从正态分布。由图3a可知：各气象站多年平均潜在蒸发量经验概率分布值并未均匀分布在正态分布概率分布曲线两侧，证实各气象站多年平均潜在蒸发量不服从正态分布。因此，选取反距离权重法绘制中国多年平均潜在蒸发量等值线(图4)。图4表明各站多年平均潜在蒸发量在686.5～2 127.8 mm/a间变化，均值为1 168.7 mm/a，低值区位于中国东北部地区，高值区处于中国西北部地区，大体由中国东部向西部地区增加。

图3 气象站多年平均潜在蒸发量、年潜在蒸发量倾向率概率分布Fig.3 Probability distribution curves of mean annual ETp and ETp’s tendency rates

2.1.3中国年蒸发能力时程演变规律

(1) 中国年蒸发能力的趋势

选取气象站历年年潜在蒸发量，计算其与时间变量间的倾向率。采用Lilliefors检验和概率分布曲线(图3b)检验各站倾向率(显著性水平为0.05)。经检验，Lilliefors检验检验值为1，尺度参数为0.001，年潜在蒸发量倾向率不服从正态分布；图3b表明：各站年潜在蒸发量倾向率经验概率值并未均匀分布在正态分布概率分布线两侧，再次证实年潜在蒸发量倾向率不服从正态分布。基于ArcGIS平台，选取反距离权重法绘制中国年潜在蒸发量倾向率等值线(图5)。图5表明，各站年潜在蒸发量倾向率在-32～21.4 mm/(10 a)间变化，均值为-3.3 mm/(10 a)，低值区位于中国东部和新疆中部地区，高值区处于中国中部和新疆东部地区，大体呈现中部较高、东西部较低的空间分布特征。

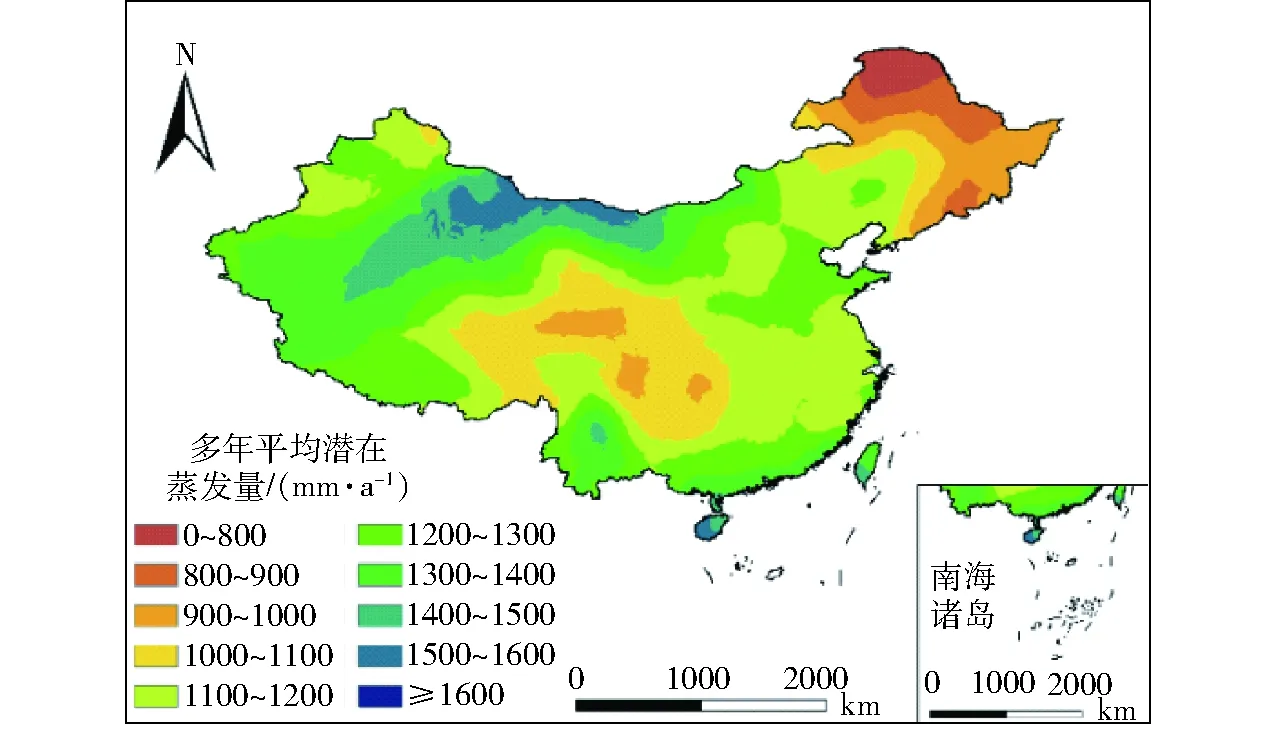
图4 中国多年平均潜在蒸发量等值线Fig.4 Contour of mean annual ETp in China

图6 气象站年潜在蒸发量突变点Fig.6 Change points of annual ETp at meteorological stations

图5 中国年潜在蒸发量倾向率等值线Fig.5 Contour of annual ETp’s tendency rates in China

(2) 中国年蒸发能力的突变

针对年潜在蒸发量趋势显著气象站，采用Pettitt和Mann-Kendall方法对各站逐年年潜在蒸发量进行突变点检验(显著性水平为0.05)，合并相近突变点，见图6。图6表明，年潜在蒸发量突变年份集中于1969—2005年间，均值为1987年。仅含1个突变点的站点比例最高，达到66%；含2个突变点的站点比例为31%；含3个突变点的站点比例最低，仅为3%。基于各站第1至第3潜在蒸发量突变点，分别采用众数滤波、焦点统计方法和突变点代际分布比例表征突变点的时空变化，见图7。图7表明：时间上，突变年份主要集中于20世纪80年代，代际占比51%，90年代占比23%，其余代际占比均为13%。空间上，突变年份出现在1990年之后的区域主要分布在中国中部地区、东北部分地区和新疆与西藏的西部地区；突变年份在1979年之前区域主要集中于中国东南地区；突变年份为20世纪80年代区域广泛分布于全国。

2.2 气象站日蒸发能力一阶差分值及其模拟

2.2.1气象站日蒸发能力一阶差分值

针对年潜在蒸发量趋势显著且存在突变点的气象站，选取各站逐日潜在蒸发量，计算各站逐日潜在蒸发量向前一阶差分实测值(ΔETpo)，见图8。图8表明，各气象站逐日潜在蒸发量一阶差分值在-12.1～13.6 mm/d间变化，均值为-2.9 mm/d，均方根误差为0.33 mm/d。

2.2.2气象站日蒸发能力一阶差分值模拟

选取各气象站逐日地表净辐射量、气温、风速和相对湿度数据，计算各站诸要素逐日向前一阶差分值和偏导数，采用彭曼公式全微分日求积方程，模拟各站日潜在蒸发量一阶差分模拟值。采用线性回归方程、决定系数及其临界值、t检验值及其临界值检验模拟效果(显著性水平为0.05)，见图8。图8表明，各站逐日潜在蒸发量一阶差分模拟值(ΔETps)相对实测值线性回归系数为0.96，决定系数及其t检验值分别为0.996和42 277，分别超过决定系数和t检验临界值(分别为0.000 7和1.96)。结果表明各站模拟与实测逐日潜在蒸发量一阶差分值线性相关，回归系数接近1，截距接近0，模拟效果较好。

图7 中国年潜在蒸发量突变年份时空分布Fig.7 Temporal and spatial distributions of change points derived from annual ETp in China

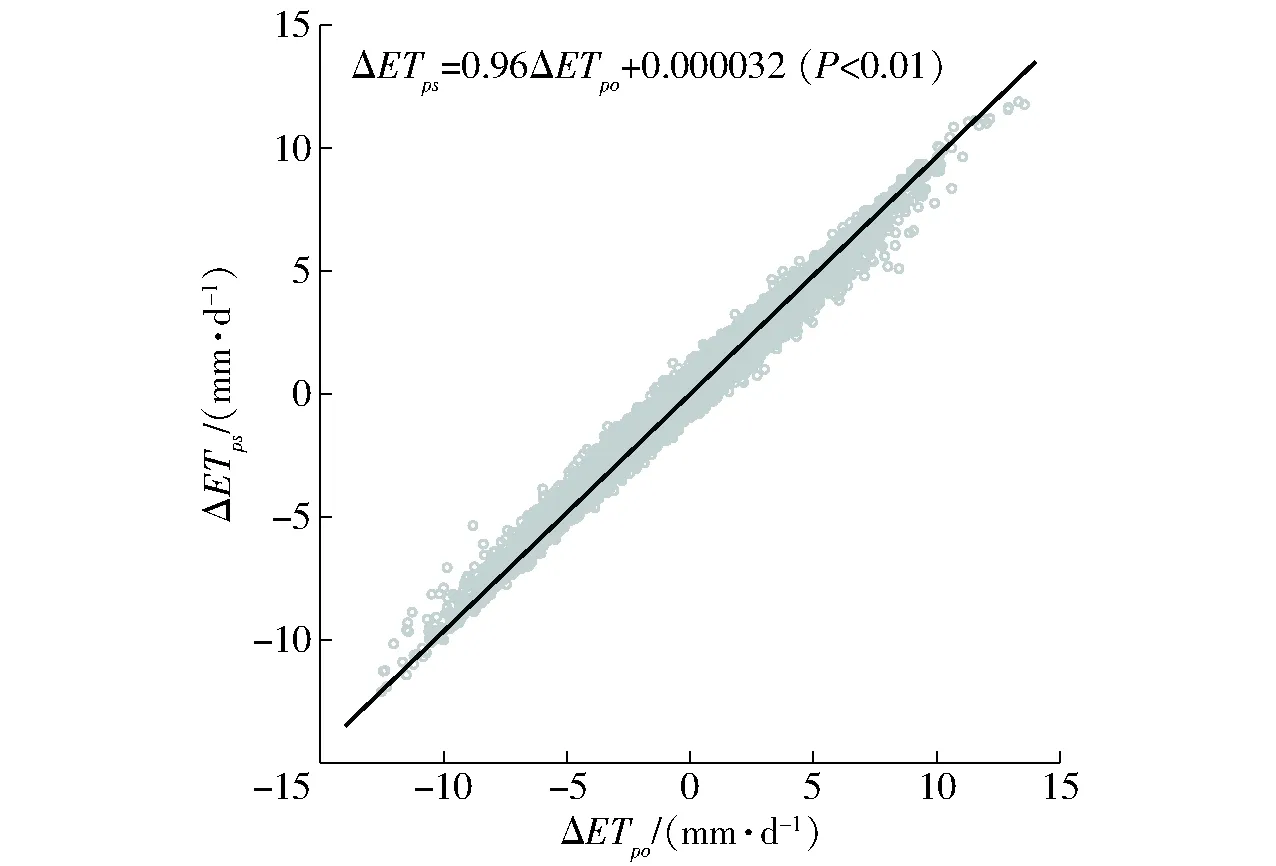
图8 气象站日潜在蒸发量一阶差分值模拟Fig.8 Simulation of daily ETp’s first-order differences at meteorological stations

2.3 中国多年平均日蒸发能力变化成因

2.3.1年均日蒸发能力变化及成因定性分析

依据各气象站年潜在蒸发量突变年份将研究时段(1961—2015年)划分为相邻时段，结合各站诸气象要素对该站日潜在蒸发量一阶差分值贡献量，计算各气象要素对该站年均日潜在蒸发量一阶差分值的贡献量，见图9。由图9a可知，各站年均日潜在蒸发量差分值在-0.77～0.48 mm/d间变化，均值为-0.13 mm/d，均方根误差为0.21 mm/d；差分值为正区域主要出现在西经98°～104°范围内，其余区域差分值整体为负值。结果表明：中国年均日潜在蒸发量整体减少，各站差分值差异较大；空间上，年均日潜在蒸发量在中部地区大体增加，在东西部地区大体减少，与年潜在蒸发量趋势空间分布吻合。

由图9b可知，各站温度、风速、净辐射量、相对湿度贡献的年均日潜在蒸发量差分值均值分别为42.6、17.3、-55、-5 mm/d；空间上，温度和净辐射量贡献的差分值在全国尺度分别大体为正值和负值；风速贡献的差分值在西经114°～125°间大体为正值，其余区间大体为负值；相对湿度贡献的差分值在西经106°以西大体为负值，以东大体为正值。结果表明：净辐射量的减少和温度的增加分别在全国尺度上引起潜在蒸发量的减少和增加；风速变化引起潜在蒸发量于东部减少，中西部增加；相对湿度变化引起潜在蒸发量于东部增加，西部减少。结合年潜在蒸发量趋势的空间分布定性判断其变化成因，可知中国中部潜在蒸发量增加可能由温度和风速的增加所致，东部潜在蒸发量减少可能由净辐射量和风速的减少所致，西部潜在蒸发量减少可能由相对湿度增加和净辐射量减少所致。

2.3.2年均日蒸发能力变化成因定量分析

基于各站实测年均日潜在蒸发量一阶差分值及气象要素相应累积贡献量，分别计算各站诸要素对年均日潜在蒸发量变化的累积贡献率；选取各站最大累积贡献率相应要素作为该站年均日潜在蒸发量变化主驱动要素；采用众数滤波、焦点统计方法对主驱动要素进行区划，计算气象要素分区累积贡献率，甄别分区主驱动要素，定量揭示各分区年均日潜在蒸发量变化成因，见图10。图10表明，依据区域年均日潜在蒸发量变化主驱动要素，将中国划分为中部、东部和西部3个区域(分别对应图10上区域1、区域2、区域3)，相应年潜在蒸发量分别整体呈现增加、减少和减少趋势。在中国中部，分区各站温度和风速累积贡献率均值分别为355和121，地表净辐射量和相对湿度累积贡献率均值分别为-305和-150，说明该区年潜在蒸发量增加成因是温度和风速的增加；在中国东部，分区各站地表净辐射量和风速累积贡献率均值分别为280和31，温度和相对湿度累积贡献率均值分别为-224和-85，说明该区年潜在蒸发量减少成因是地表净辐射量的减少。在中国西部，区域各站相对湿度和地表净辐射量累积贡献率均值分别为175和88，温度和风速累积贡献率均值分别为-24和-239，说明该区潜在蒸发量减少成因是相对湿度的增加。

图10 多年平均日潜在蒸发量变化气象要素贡献率及驱动要素区划Fig.10 Driving force and its contribution’s regionalization of changes in mean annual daily ETp

3 讨论

3.1 中国年蒸发能力动态的成因

由彭曼公式可知，以潜在蒸发量表征蒸发能力，蒸发能力受地表净辐射量、气温、风速和相对湿度支配。蒸发能力及其相关气象要素的动态，在不同空间尺度受全球和区域气候事件、地形和地理等要素影响，呈现不同随机性和演变规律。当空间尺度较小时，全球和区域气候事件影响相对有限，蒸发能力变化受局部微地形影响显著，其变化表现出较高随机性；随着空间尺度增大，随机性减少，蒸发能力变化在大尺度空间呈现一定稳定性，表现为特定区域特征。例如中国年潜在蒸发量变化的区域特征为中部增加，东部和西部减少。

基于中国年潜在蒸发量的时空变化，结合地理和气候特征，提出年蒸发能力时空动态的可能成因。中国中部年潜在蒸发量增加，其空间范围分布在大兴安岭-阴山-贺兰山-巴颜喀拉山-冈底斯山两侧。这些山脉将我国划分为季风区和非季风区，山脉东南侧为季风区，西北侧为非季风区。中国东南部距海洋较近，海陆间物质和能量交互作用强烈，该区蒸发能力动态更多体现全球气候事件影响。中国西北部距海洋较远，海陆间物质和能量交互作用较弱，该区蒸发能力动态更多体现全球和区域气候的综合影响。

3.2 气象站日蒸发能力动态模拟时间尺度效应

理论上，分析时段选取越小，全微分积分路径对气象要素变化过程的概化就越接近真实，气象要素对潜在蒸发量变化的贡献率计算就越准确。但是，在现有实测气象数据库中，获取资料完整、数量充足的小时或更短时段数据存在困难。本文采用日为积分路径时间尺度，可较为准确地概化气象要素变化过程，获取气象要素的累积贡献率，保证结果可信。但是为验证彭曼全微分公式求积方程模拟效果对分析时段的敏感性，尚需进一步选取气象站实测分钟、小时数据进一步验证。

3.3 中国年均日蒸发能力变化对全球、区域气候变化的响应

针对区域蒸发能力变化成因，现有研究多采用行政边界分区[28]，难以对区域蒸发能力变化规律形成整体认识，所得结论有待商榷。本文对各气象站蒸发能力动态的主驱动因子进行区划，证实中国东部和西部多年平均日蒸发能力减少最主要成因分别是地表净辐射量减少和相对湿度增加。中国中部多年平均日蒸发能力增加最主要成因是温度的升高。由于中国东部、中部受全球气候变化影响较大，东部地表净辐射量减少推测为全球暗化诱发[29-30]，中部温度升高推测为全球变暖诱发[31-32]。由于中国西部受区域气候变化影响较大，受全球气候变化影响相对较小，相对湿度增加推测为区域降水增加诱发[33]。

本文对蒸发能力动态的气象要素贡献进行了定量分析，并探讨将其定性归因至全球和区域气候变化。但对区域蒸发与气候边界条件间的耦合关系缺乏认识，尚需进一步定量研究。

4 结论

(1)A-P模型参数a在0.47～0.69之间变化，平均值为0.55，最大和最小值分别出现在甘肃武威站和新疆阿克苏站；模型参数b在0.13～0.29之间变化，平均值为0.19，最大和最小值分别出现在新疆库车站和浙江慈溪站。模型模拟和实测地表辐射量均方根误差平均值为2.48 MJ/(m2·d)，Nash-Sutcliffe效率系数平均值为0.88，模拟精度较高。

(2)各气象站多年平均潜在蒸发量在686.5～2 127.8 mm/a之间变化，均值为1 168.7 mm/a，低值区位于我国东北部地区，高值区处于我国西北部地区，大体由东部向西部地区增加。各气象站年潜在蒸发量倾向率在-32～21.4 mm/(10 a)之间变化，均值为-3.3 mm/(10 a)，低值区位于东部和新疆中部地区，高值区处于中部和新疆东部地区，大体呈现东西部较低、中部较高的空间分布特征。各气象站年潜在蒸发量突变年份均值为1987年。综上可知：我国年潜在蒸发量大体自1987年起显著减少。

(3)采用彭曼公式全微分日求积方程，模拟逐日潜在蒸发量一阶差分值。模拟相对实测值回归系数为0.96，决定系数和t检验值分别为0.996和42 277，分别超过各自临界值。模拟与实测值线性相关，模拟效果较好。

(4)各气象站年均日潜在蒸发量差分值在-0.77～0.48 mm/d之间变化，均值为-0.13 mm/d。空间上，年均日潜在蒸发量于我国中部地区增加，一阶差分值大体为正值，由温度和风速增加所致，相应区域累积贡献率分别为355和121；年均日潜在蒸发量于中国东部和西部地区减少，一阶差分值大体为负值，东部年均日潜在蒸发量减少由地表净辐射减少所致，相应区域累积贡献率为280，西部年均日潜在蒸发量减少由相对湿度增加所致，相应区域累积贡献率为175。