离散数据挖掘方法改进措施探究

石宜径

（兰州财经大学统计学院2016级应用统计专业，兰州 730101）

数据挖掘就是从一系列庞大的数据体系中，通过采用一定的科学方法来获得有用的信息，进而对我们的生产生活起到帮助作用。但是现实生活中，有诸多因素影响到数据的形成过程，采集过程。并且经过研究发现，诸多数据的属性都具有极大连续性，即我们所说的连续属性，因此将其进行离散化具有重要意义[1]。这就是数据的预处理，所以数据的预处理就是将所获取的比较杂乱的数据经过信息提取，获得有效信息的过程。我们都知道获取的数据都具有连续属性，对其进行离散化成为在数据挖掘之前非常重要的一步，这种操作对信息进行提取，不仅减小了数据量，使之经提取变成有用信息，而且还能提高数据模型的运行效率和结果优化，呈现更准确的数据结果。在名词属性中，大致可以分为三类：名词属性、数字属性和连续值属性。尤其注意的是，在数据处理过程中，大多数处理的是具有离散值属性的数据集合，当然也有些既可以处理这些，也可以处理连续值属性，这时候就出现一个问题，连续值属性的处理结果会比离散值属性结果差很多，因此我们要想获得好的成果，就应该进行离散化处理，在这里我们应该注意离散化程度应该合理考虑数据情况与使用情况相结合，以达到处理的最佳结果。本文主要是对连续属性数据离散化进行了解，分析自由度并提出改进算法，最后应用于实例中。

1 现状

由于机器学习和数据挖掘技术的逐步深化，对连续属性进行离散化越来越成熟，也有了很大的发展，但是到目前为止，仍然出现市场较为混乱，模型精度参差不齐，结果也不一。在1990年Chiu等人基于在离散化空间中提出熵最大的原理来形成的，就是在此空间中通过应该较为科学的搜索法来获得较为合格的分区，尤其注意的是该算法需要西安选择得到比较合适的初代分区，而该分区能够影响后面的分类精度。随后有科学家提出了基于信息熵的方法，涉及到了决策树的引入，需要用到迭代回归分析方法，为保证结果的有效性，需要在数据处理中引入前提条件，一般有这三种条件：最小信息增益、最小示例数和最大分区数。

到目前为止，研究学者主要对老旧算法进行了一定程度上的改进，相应也取得了显著效果。比如说较为普遍的概率生成模型，该模型是依靠概率知识进行数据离散化，成果显著提高[2]。其他有些方法是计算机工具提供的，较为死板，不值得提倡。对部分模型是经过其他专业领域经过直接采用所形成了，但很难被数据挖掘人员使用，不能很好普及。在这里值得一提的是基于粗糙集理论和布尔逻辑的属性离散化方法，该方法的优点在于完全吸收了粗糙集理论的优势与发挥布尔逻辑的优点，使得离散化结果更加具有可信性[3]。

2 基本原理

对数据进行离散化，就是依靠一些依据来对数据进行分类获得所需结果。在生活中，最常见的就是按照学生的成绩来进行划分，分为不及格与及格学生名单。而又将及格名单可以进一步分为良好、优秀等不同区间。就比如依据年龄对人群进行划分：儿童、少年、青年、中年、老年等。更远的，还可以按照其他标准参数来划分原始数据，例如身高、体重等等，相同的分类方式，不同的分类依据，也会得到不同的结果。

决策表定义为：设S=＜U，R，V，f＞为一信息系统，其中U={x1，x1，…，xn}是论域，A是属性集合，V是属性取值集合，F是U*A→V的映射。若A=C∪D，C∩D=Ø，C称为条件属性集，D称为决策属性集，则该信息系统称为决策表。一个决策表S=＜U，R，V，f＞，其中R=C∪{d}是总的属性集合，子集C是条件属性集，是决策属性集，{d}是决策属性，U={x1，x1，…，xn}是论域。属性a的值域Va上的一个断点用（a，c）表示，其中c是实数集，a ∈ R。在值域 Va=[Ia,ra]上的任意断点区间定义了V的一个分类pa：

对于任意pa=Upa定义了新的决策表，SP=＜U，R，VP，f ＞fP其中xa∈U，i∈{0，1，…，Ka}，会形成新的信息。

属性离散化的一般步骤如图1所示：

图1 属性离散化步骤

3 离散化算法

（1）等宽区间法。该方法是最简单的算法，讲的是数据按照等间隔划分得到等间隔数列，最后每个数据的间隔都是相等的，但是对于离散却隐约符合正态分布或其他分布的数据却不太好。因为一般数据都趋向于某一数值，并且呈现出大量集中于某一块或某一范围的现象，对这种情况可以适当考虑等频区间法。

（2）等频区间法。这个算法的优点在于等频，就是在区间内我们可以放入等多的数据，这些数据的数量是一样多的，在一定上可以避免数据大量集中的问题，这个方法与上一个方法的区别在于，两者都是等间隔，不同的是一个是等宽度，一个是等数量，两者各有优劣，在具体使用中应该尤其注意。而且这两种算法比较简单，会使得处理结果较差，应该与其他高级算法结合，以达到所需效果。

（3）k-means算法。该算法比较常用，相对于上两个算法，会更加高级与科学，尤其注意在算法运行前需要属于分组个数。该算法的核心算法在于，先找到样本的重心，然后以欧氏距离为依据来进行样本划分，然后重新计算重心再进行划分，最后直到不再分类为止。在这里我们应该提前了解数据，对分类数量以及阈值有个设定，才能使分类结果更好。

4 基于自由度的离散化方法

4.1 卡方分布

χ2分布：设X1，X2，…Xn是来自总体N（0，1）的样本，则称统计量

服从自由度为n的χ2分布，自由度指的是样本个数。

4.2 Extended Chi2算法

Su等人在2005年提高了Modi fi ed Chi2算法，因为他认为原作者使用D的时候没有考虑到实际分类过程中的差异，应该在获得D的基础上除以，来得到更为可靠的结果，即Extended Chi2算法[4]。该算法的步骤如下：

首先计算数据的不一致率，然后根据属性值来进行升序排序处理，计算所有数据的χ2值，再结合具体的α数值来得到实际的Xα2数值，然后我们就可以得到D。然后执行迭代算法，当邻区间不能再合并时结束循环，这时候再参考不一致率情况，如果不变则跳转到计算D，否则进入下一步，即跳出迭代的合并。然后用新的α来代替旧值，算出D，并查阅是否可以将级，如果不能则跳出循环结束。最后，对所有属性进行离散化，采用逐步运算方法，并参考不一致率。

5 基于改进自由度的离散化方法

在之前的算法中，我们是将自由度为k-1，对于上述算法。再后来的算法则是讲自由度改为k′-1，而将k改为类别数。χ2分布的随机变量：

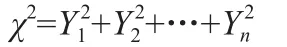
因此我们可以得出这样的结论：自由度选取与类别数和相临区间数是有关的，故而可以选2k-1作为自由度，k为系统的类别数。

6 结果验证

UCI数据库是加州大学欧文分校提出的用于机器学习的数据库，这个数据库暂时共有335个数据集，但还在增加。从该数据库中随机选取7个数据集进行验证。如表1所示。

表1 数据集相关属性统计表

对基本算法与改进算法用matlab进行编程，对7个数据进行处理（离散化），统计识别出正确识别率精度以及形成规则的平均个数，从表2中可以清楚看出，对于大多数数据，采用自由度改进算法进行处理，会使处理结果更好，说明改进算法有效。

表2 处理结果表