垂直丝网附近单个可变形气泡上升运动研究
2019-02-14陈叶宇凃程旭包福兵尹招琴高晓燕杨钦灿汪钰锟
陈叶宇,凃程旭,2,包福兵,尹招琴,高晓燕,陈 强,杨钦灿,汪钰锟
(1.中国计量大学 计量测试工程学院,浙江 杭州 310018;2.利欧集团股份有限公司,浙江 温岭 317500)

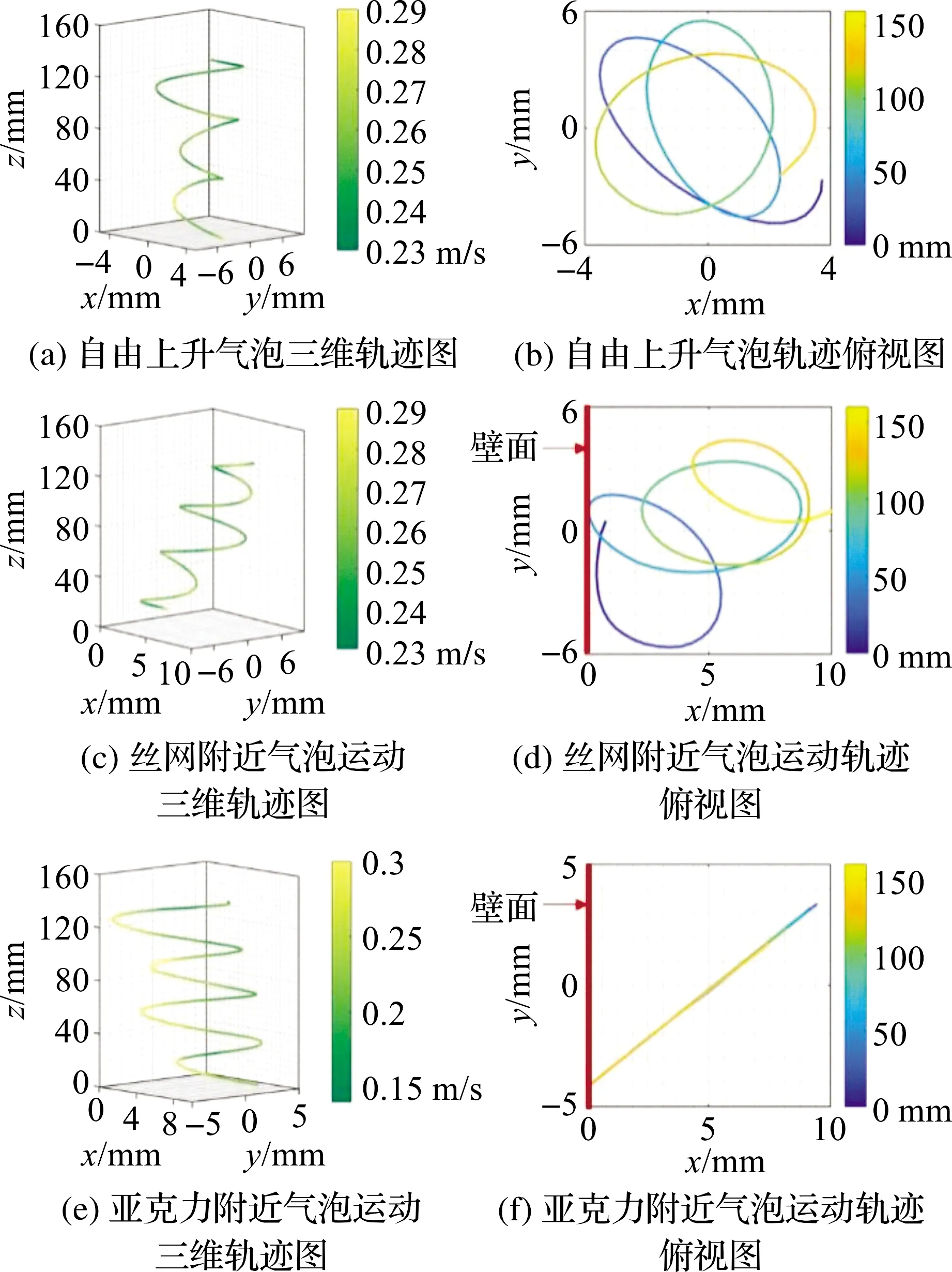
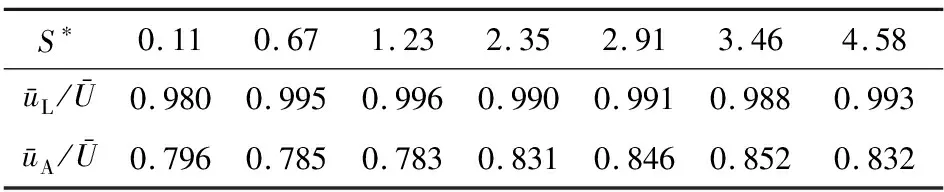
在工程应用场合中,气泡由于受到壁面边界的影响,当Re>O(102)时,近壁气泡开始沿壁面做周期性弹跳运动。MOCTEZUMA和ZENIT[9]基于势流理论对高Re数(200 尽管前人已做过许多相关研究,但是对于近壁气泡动力学研究仍然有必要。考虑到之前针对近壁可变形气泡的研究较少,且壁面多为无滑移条件;对于可渗透壁面对气泡运动的影响之研究尚不多见。本文以金属丝网代替传统不可渗透亲水壁面,搭建近壁气泡运动实验台,观察多孔结构壁面对气泡运动的影响,特别是上升路径、速度等运动特性的变化,以便能够进一步理解可渗透壁面对可变形气泡上升路径失稳的影响,为预测或者控制可变形气泡在壁面附近的空隙率分布提供实验基础。 实验装置如图1。其中,本实验采用的容器为亚克力长方体水箱(600 mm×600 mm×600 mm),水箱内充满自来水,实验水温(18.5±1)℃。注射泵(Harvard Pump 11 Elite)通过毛细管连接位于水箱底部中央的不锈钢喷嘴(内径1.26 mm)释放气泡,注射泵流量为0.1 mL/min。通过测量计算自由上升气泡相关参数,确定实验气泡为可变形扁椭圆气泡,其等效直径deq=3.53 mm,平均上升速度为0.228 m/s,对应的Re数以及Eö数分别约为800和1.74。 图1 垂直丝网附近气泡上升运动实验装置 采用304不锈钢丝网作为参考壁面,丝网网孔形状为方形,具体丝网参数如表1。由于表面张力作用,气泡在此丝网附近运动时会被丝网阻挡,无法穿透丝网[12-13]。通过改变丝网与喷嘴出口中心之间的距离,即气泡中心与壁之间的初始距离S*(S*=S/req)研究上升气泡的运动特性,其中,S为实际丝网与喷嘴中心之间的初始距离,req为气泡等效半径。金属丝网壁面(550 mm×500 mm)竖直放置在水箱内。 表1 丝网参数 气泡的形状和上升路径由两台高速相机(FASTCAM Mini UX,Photron)同时捕捉,高速相机采集频率为2 000帧/秒,分辨率为1 280×1 024 pixels。拍摄平面位置位于喷嘴出口上方20 cm处,此时,气泡轨迹在此过程段均为三维螺旋形气泡接近其终了速度并且速度波动较为稳定[14]。为了定量分析气泡运动特性,通过Matlab自编程序以及Image J处理,获得气泡大小以及坐标。由于表面张力的作用,附着在喷嘴尖端的不断增长的气泡近似为轴对称,因此可以通过基于高速阴影技术提取气泡边缘获得确切的气泡尺寸。通过测定气泡脱离喷嘴时的尺寸,可以将产生的气泡的体积不确定度控制在3%以内,由此假设气泡体积保持不变。由校准的气泡体积计算得出气泡的体积当量直径deq为3.53 mm。此外,两个平面内测量的“短”轴并非气泡短轴的真实投影[15],为此通过体积反求气泡实际短轴。 我们对每种工况分别进行5~10组重复实验,排除由于气泡释放方式引起的粗大误差,并求取平均值减小随机误差。图2为自由上升气泡、初始近壁距离S*=0.11下气泡分别在丝网L以及亚克力壁面附近运动的上升轨迹。在丝网附近运动的气泡,其上升轨迹仍为三维螺旋形,与自由上升气泡运动轨迹类似,从俯视图2(d)中可以观察到气泡与壁面发生碰撞。仅当初始距离S*为0.11时,在丝网L附近运动的气泡出现多次周期性弹跳运动。随着S*的增加,气泡并未与丝网壁面发生碰撞,并且运动趋势类似,均保持三维螺旋运动。对比气泡在不可渗透普通壁面(亚克力)附近上升情况图2(e)~(f),气泡在S*为0.11时,运动路径转捩为二维之字运动,与壁面碰撞剧烈。由于气泡的非周期性波动使得气泡并未垂直撞击壁面,而是以一定角度接触亚克力壁面。随着S*的增加,气泡与壁面碰撞情况仍然存在,逐渐远离壁面后气泡又逐渐从二维之字运动重新回到三维螺旋运动,此时气泡不再与壁面碰撞,运动路径为非周期振荡。对比图2(a),2(c)和2(e)中发现不同边界条件下气泡运动路径振荡周期f发生变化,f亚克力>f丝网>f自由运动。由于壁面存在限制了气泡在x-z方向上的运动,使得路径振荡频率出现跃迁;此外,由于亚克力壁面的不可穿透性使得阻尼效应大于丝网壁面,因此气泡在亚克力附近运动的轨迹振荡周期最大。 图2 自由上升气泡与S*=0.11时气泡在不同壁面附近运动轨迹图 气泡在尾流的作用下会出现路径失稳,但是以螺旋形式上升的气泡后方会产生一对同样以螺旋形路径缠绕扭转在一起的流线涡[16-17],结构较为稳定。结合在丝网附近上升的气泡在运动过程中没有发生三维螺旋到二维之字运动的转捩情况,说明在与丝网碰撞的过程中气泡尾流中的涡结构并未发生巨大变化。而在普通壁面附近运动气泡,以之字形运动过程中其后部往往伴随着发夹涡流的脱落[2]。 图3 气泡在不同壁面以及近壁距离下的运动轨迹图 我们通过测量轨迹上峰峰值之间的距离以及各个峰值的振幅,将结果平均后得到气泡平均振幅和波长,而不是仅仅通过拟合函数计算轨迹波长与振幅[18-19],即使气泡轨迹近似于sin函数波动。其中,测量得到自由上升气泡的无量纲参数:波长(λ*=λ/req)与振幅(h*=h/req)分别为24.2和4.41。如表2,在丝网附近上升气泡整体的λ*与h*要略小于自由上升气泡。当S*=0.11时,丝网L附近上升的气泡在弹跳过程中其λ*与h*明显小于自由上升气泡附近的情况,使得气泡的弹跳周期增加,即,在同样的上升时间内,在丝网附近运动的气泡其路径振荡周期大于自由上升气泡下的情况;当S*>0.11后,λ*与h*逐渐上升,趋向回到自由上升情况下的波动情况,路径振荡周期略有下降。随着近壁距离的增大到S*为4.58时,λ*整体波动幅度较小,波动稳定在22附近,此时丝网对于气泡运动仍有一定的影响。 表2 不同近丝网距离下气泡运动波长与振幅 显然,边界条件的改变即壁面的存在,气泡轨迹会出现一定的波动,当气泡与丝网壁相互作用的时候无法存在同自由上升时一致的涡结构,致使气泡在上升过程中轨迹发生变化;另一方面,对于多孔结构来说,由于非零液相速度以及切向滑移耦合使得气泡产生横向位移[20]。即当周围液体静止且多孔壁面上液体流动仅由气泡运动引起时,切向滑移边界使气泡远离壁面;液体在渗透过程中,法向速度非零使气泡朝向壁面运动[11]。因此,在丝网壁面附近运动的气泡整体波动要略小于自由上升时的情况,本文将在2.2节详细分析速度的变化情况。 图4显示了气泡在不同壁面附近上升过程中侧面(x-z)与正面(y-z)两个平面内的瞬时法向速度(vx,vy)以及瞬时上升速度u的变化情况。由于气泡横向迁移使得上升速度u与法向速度相比波动相对平缓。对于弹跳气泡来说,气泡受到吸引朝丝网壁面运动时,法向速度vx在碰撞前达到负向最大值,在碰撞过程中法向速度vx迅速减小至零,随后气泡朝远离壁面方向运动,vx随之改变方向朝正向峰值方向增大。当气泡在碰撞后运动到距离丝网最远端时,vx几乎保持恒定,并且在之后的弹跳运动中重复相同的过程。每次碰撞之后,u,vx,vy没有显著减小。法向速度波动周期近似上升速度波动周期的2倍,近似路径振动周期[9]。 图4 S*=0.11时气泡在不同壁面附近运动的速度图 当运动时间t小于0.16 s时,气泡未与亚克力壁面碰撞,从图3(b)中可以明显看到法向速度vy出现波动;当t大于0.16 s时,气泡朝亚克力壁面运动随之与壁面发生碰撞,螺旋运动近似转捩为二维运动,在y-z平面内近似直线运动,因此法向速度vy接近为零。在x-z平面内,气泡与壁面碰撞,vx波动趋势同气泡-丝网碰撞情况一致。此时气泡仅在x-z平面内振荡,上升速度u波动较为明显。 为了进一步研究边界条件对气泡上升速度的影响,将不同壁面附近气泡的平均上升速度ū与自由上升气泡平均上升速度进行比较,如表3所示。因为壁面边界的存在,气泡上升速度要小于自由上升气泡的平均速度,即ū/<1。其中,ūL/为气泡在丝网附近运动的平均速度与自由上升气泡的平均速度的比值,ūA/为气泡在亚克力附近运动的平均速度与自由上升气泡的平均速度的比值。对于多孔结构,不同S*对气泡平均上升速度的影响较小,ūL/在0.98附近波动。注意到S*=0.11时,ūL/最小,但与其他近丝网距离下气泡速度相比偏差不是很大,速度损失小于2%。然而,气泡在亚克力壁面附近上升时,其平均上升速度比范围为0.80~0.85,上升速度损失明显大于丝网壁面。由于亚克力为不可渗透的非滑移壁面,气泡和壁面之间存在一层液膜,撞击过程中气泡需要排开液膜[21];此外,不可渗透的壁面干扰会影响壁面诱导的尾流修正,产生较大的粘性耗散[11]。 在液相非静止的情况下,气泡倾向于在来流方向保持自身倾角而不再发生变化[10];在液相静止的情况下,当气泡运动到距离壁面最远端或者最近端,即轨迹的峰值或峰谷处时,气泡倾向于呈水平状,即其两个方向的长轴与x轴以及y轴平行,随后由于气泡尾流涡不对称以及液相非零法向速度相互作用[11],导致气泡运动方向改变,气泡沿朝向壁面或远离壁面运动,使得气泡倾角随着运动方向变化而变化。 表3 不同壁面以及近壁距离下气泡平均上升速度比 Table 3 The mean rise velocity(ū/)of a bubble rising near different walls withS* S∗0.110.671.232.352.913.464.58ūL/Ū0.9800.9950.9960.9900.9910.9880.993ūA/Ū0.7960.7850.7830.8310.8460.8520.832 在气泡-丝网碰撞过程中,气泡倾角β的波动范围在±35°,孔隙率对β影响较小。当壁面为海绵,亚克力板以及聚四氟乙烯时,β的波动范围分别在±30°,±17°和60°[11],发现多孔结构下β变化范围较为吻合。对于亲水壁面,β变化明显小于疏水壁面,运动过程中所需的角动量较小,即气泡在弹跳过程中发生旋转的情况较少。对于可变形气泡特别是大扁椭圆形气泡,气泡形状在上升过程中不断发生变化,在x-z和y-z两个平面内的长轴a和短轴c均发生变化,导致纵横比χ(χ=a/c)发生变化,从而影响气泡运动附加质量以及速度[11,22]。因此,理解纵横比变化规律有助于预测气泡运动状态。 图5 S*=0.11时丝网L附近气泡纵横比变化 本文通过改变初始气泡壁距离,测量并分析了可变形气泡的近丝网上升行为,结论如下。 1)气泡在丝网附近上升轨迹呈螺旋形,运动路径并未出现转捩,在最小间隙S*=0.11处,气泡与丝网发生碰撞进行弹跳运动并且在该位置附近上升的气泡其振幅和波长最小。 2)丝网具有较强的非零正向速度以及可滑移的壁面特性,对比传统不可穿透壁面(非滑移壁面特性),丝网对气泡运动特性的影响较小,气泡上升速度损失较小且平均上升速度对S*变化不敏感。 3)碰撞情况下气泡在丝网附近运动过程中纵横比与法向运动路径近似耦合。1 实验设计
1.1 实验装置


1.2 图像拍摄和数据处理
2 气泡运动特性
2.1 气泡运动轨迹


2.2 上升气泡瞬时速度

2.3 碰撞情况下气泡倾角变化以及变形情况
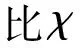

3 结 论
