基于替代模型的地下水DNAPLs污染源反演识别

侯泽宇,卢文喜*,王 宇



基于替代模型的地下水DNAPLs污染源反演识别

侯泽宇1,2,卢文喜1,2*,王 宇1,2

(1.吉林大学,地下水与资源环境教育部重点实验室,吉林 长春 130021；2.吉林大学环境与资源学院,吉林 长春 130021)

应用基于核极限学习机替代模型的模拟-优化理论和方法研究解决了地下水DNAPLs污染源及含水层参数的同步反演识别问题.结果表明:1)核极限学习机替代模型对模拟模型有较高的逼近精度,能够识别并模仿模拟模型的输入-输出关系,绝大部分相对误差小于5%,平均相对误差仅有2.98%;2)以替代模型代替模拟模型,大幅度地减小了模拟-优化过程的计算负荷,将反演识别时间由传统方法的83天减少到3小时,并能够保持较高的计算精度;3)应用基于模拟退火的粒子群优化算法求解优化模型,能够以较快的速度搜寻到全局最优,同时避免搜索过程陷于局部极小解.

DNAPLs；污染源反演识别；模拟-优化；多相流模拟；核极限学习机替代模型

石油类有机污染物在水中的溶解度一般很小,进入含水层后通常以非水相流体(Non-Aqueous Phase Liquids, NAPLs)的形式存在.在与水接触的过程中,NAPLs会不断向水中溶解释放.密度大于水的重非水相流体(Dense NAPLs, DNAPLs)具有高密度、低水溶性和高界面张力的特性,实际修复过程中,常常面临污染物去除率低、修复过程时耗长和修复费用昂贵的困难[1].因此,制定合理高效的修复方案就显得尤为重要.而合理高效修复方案的制定则要以对于含水层中DNAPLs污染源状况的识别和掌握为前提.

由于地下水埋藏于地下岩土介质之中,地下水污染通常具有存在的隐蔽性和发现的滞后性特点,致使人们对于地下水污染源的状况都缺乏了解和掌握.这给地下水污染修复方案设计、风险评估和污染责任认定都带来了很大的困难.因此,有关地下水污染源反演识别的研究就显得格外重要[2-3].

地下水污染源反演识别是指根据有限的地下水污染监测数据,反演求解描述地下水污染的数学模拟模型,从而识别确定地下水污染源的个数、空间位置和释放历史等相关信息[4-5],在数学上属于数理方程反问题(或称数理方程反演问题).相对而言,数理方程的正问题(或称正演问题)具有较长的研究和应用历史.正演问题一般都属适定性问题,是发展较为完善的问题.而反演问题的发展历史相对较短,兴起于20世纪60年代,其理论和应用尚处于发展阶段.反演问题大都具有非线性和病态性(不适定性)的特点,原因在于求解反演问题时,已知的信息量远远少于待求的信息量,这也正是反演问题的难点之所在[6].

目前地下水污染源反演识别的研究现状和发展趋势具有如下特点:1.研究对象多为假想例子[7-10],实际例子十分少见.对于假想例子,可以假定含水层参数是已知的,只有地下水污染源的相关信息是未知待求的.而对于实际例子,不仅地下水污染源的相关信息是未知的,含水层参数也是未知的,待求变量增加.而且含水层参数与污染源之间还是相互影响的,如果含水层参数取值不准确,必然导致污染源的识别结果不准确.因此,今后需要加强对于实际例子的研究,并在反演过程中对污染源和含水层参数都要进行识别.2.模拟-优化方法目前已成为地下水污染源反演识别的主要方法之一[11].然而,若在优化模型的迭代求解过程反复调用模拟模型,会带来庞大的计算负荷,严重制约了模拟-优化方法在反演识别实际应用中的可行性,因此,研究建立模拟模型的替代模型成为近年来研究进展中的前沿问题之一[12-13].3.近年来,遗传算法、模拟退火算法、蚁群算法等启发式算法越来越多地被使用到污染源反演识别问题中[14-17].启发式算法具有全局搜索能力,但对于初始点的依赖仍较为严重[18-19].因此,尚有待于寻求不依赖于初值选择的非线性优化模型的有效解法.本文旨在运用模拟-优化反演的理论和方法,针对这些问题开展进一步的研究,解决地下水重非水相流体污染的污染源反演识别问题.

1 研究方法

地下水污染源反演识别是指根据有限的地下水污染监测数据,对描述地下水污染的数学模拟模型进行反演求解,从而识别确定含水层中地下水污染源的相关信息,包括污染源的个数、空间位置和释放历史.其中释放历史是指污染物释放强度随时间的变化过程,也就是污染物在各时段的释放强度.

针对前述地下水污染源反演识别研究现状和发展趋势中存在的问题,本文基于模拟-优化理论与方法,首先建立污染场地的多相流模拟模型,然后建立模拟模型的核极限学习机替代模型,并通过应用基于模拟退火的粒子群优化算法求解替代模型与优化模型的耦合模型,实现地下水DNAPLs污染源及含水层参数的同步识别.

1.1 模拟-优化方法

模拟-优化方法中的模拟指的是地下水溶质运移模拟模型(简称模拟模型),用来描述地下水污染源特征与监测点处污染物浓度的激励-响应关系.优化指的是优化模型,其目的是解决优选问题.对于污染源反演识别问题,模拟-优化方法是将模拟模型与优化模型耦合,即将模拟模型嵌入优化模型中,使模拟模型成为优化模型的一部分.运用启发式算法等方法对优化模型进行求解,通过不断迭代搜索污染源的位置、释放强度等变量或它们的组合,使得由模拟模型获得的污染物计算浓度与实际监测浓度最为接近.

1.2 替代模型

优化模型的迭代求解过程需反复调用模拟模型,会带来庞大的计算负荷,严重制约了模拟-优化方法在反演识别实际应用中的可行性[20],因此,研究建立模拟模型的替代模型成为近年来研究进展中的前沿问题之一.替代模型在功能上逼近模拟模型,能够以很小的计算负荷逼近模拟模型的输入-输出响应关系[21-22].本文应用核极限学习机法建立多相流模拟模型的替代模型.

核极限学习机(Kernel Extreme learning machines, KELM)将核函数引入到极限学习机(ELM)的训练中,采用核映射替代传统ELM中的随机映射,能够产生稳定的输出结果,其分类和拟合能力均优于非核的ELM方法,泛化能力和学习速度大幅提高.目前尚未见有运用核极限学习机替代模型进行地下水DNAPLs污染源反演识别的研究报道,可通过实例应用分析核极限学习机替代模型的可靠性和优缺点.

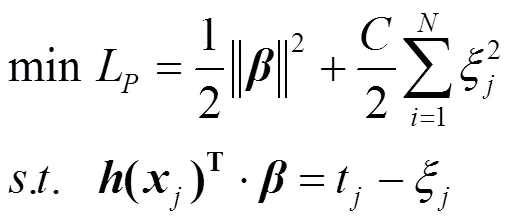
ELM的核矩阵为

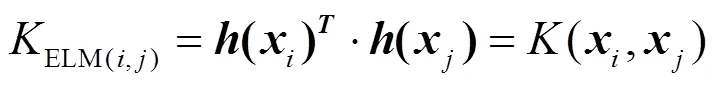
式中:是训练样本输入在特征空间的映射矩阵.

训练后的KELM输出函数表达如下:

1.3 优化模型

优化模型的一般形式为:

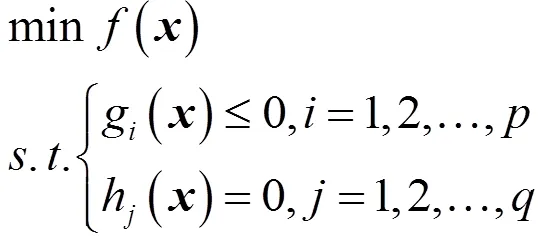
粒子群优化算法(Particle swarm optimization, PSO)是一种基于种群协作的随机寻优算法.模拟鸟群觅食行为的粒子群优化算法与遗传算法相似,通过迭代寻找最优解.

模拟退火法(Simulated annealing, SA)是一种众所周知的元启发式优化算法,模拟高温固体的退火过程.由于在搜索过程中具有概率突跳能力,模拟退火法可以有效地避免搜索过程陷入局部极小解[19].

将模拟退火法与粒子群优化算法结合,能有效吸取两种方法的优点,在不依赖于初值选择的条件下,以较快的收敛速度获得最优解,避免搜索过程陷于局部极小解.

基于模拟退火的粒子群优化算法的基本运算过程可以概括为[23-24]:

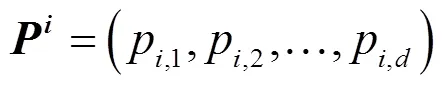
3)确定初始温度:

4)计算当前温度下各粒子的适配值:

5)计算惯性权重:

式中:max和min为的最大值和最小值,f为第个粒子当前的目标函数值,f和min为当前所有目标函数值的平均值和最小值.

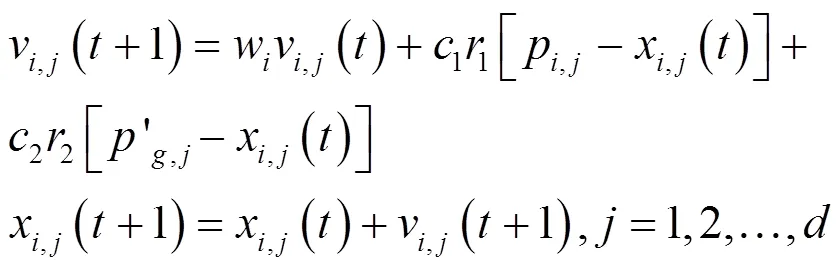
式中:1和2为0到1之间均匀分布的随机数.

7)重新计算粒子的适应度,并与之前作对比,更新pbest,gbest.进行退火操作:

式中:为退火常数.=+1,如果达到最大迭代次数,令gbest为最优解;否则返回步骤3.

2 实例研究

2.1 问题描述

以吉林省吉林市某化工污染场地为研究实例,污染很可能是由一个爆炸事故引起的.根据地下水水样测试分析结果可知,研究区孔隙潜水含水层中的地下水受到了有机污染物——氯苯的污染.收集研究区先前的相关水文地质研究项目报告,根据野外现场调查工作,了解掌握研究区的地质和水文地质条件以及地下水污染源可能的分布状况.在对已有资料充分分析的基础上,利用场地内的3口水位水质监测井开展水位、水质同步动态监测工作,每月进行一次水位、水质监测.

2.2 模拟模型的建立

计算目的层为松散岩类孔隙潜水含水层,研究区可概化为非均质、各向同性,并含有若干夹层的三维多相流模型.污染场地附近无天然边界,可在污染物迁移影响可忽略不计的地段划定边界.其中,东西边界概化为一类边界,地下水流向由东向西;南北边界由流面组成,概化为零通量边界;计算模拟区的上部为潜水面,是水量交换边界,下部为隔水层,可概化为零通量边界(图1).水和氯苯的物理化学参数详见表1.

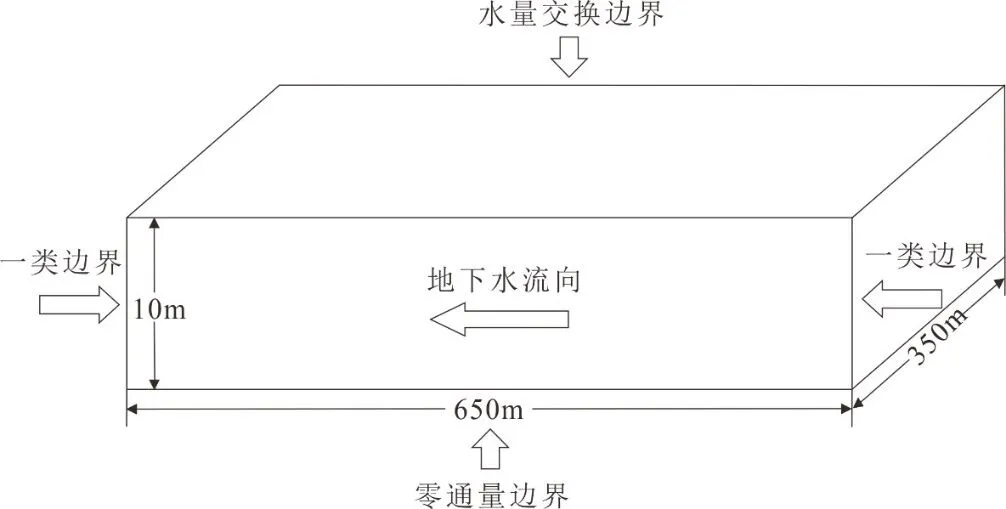
图1 计算区及边界条件

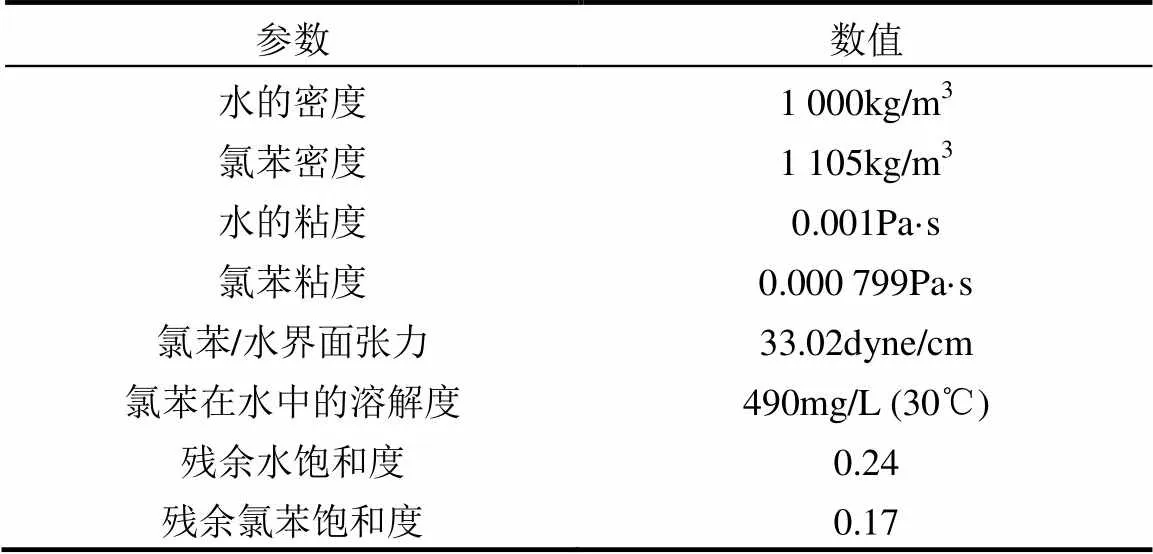
表1 水和氯苯的物理化学参数

根据污染场地的水文地质概念模型,初步建立如下多相流数学模型:

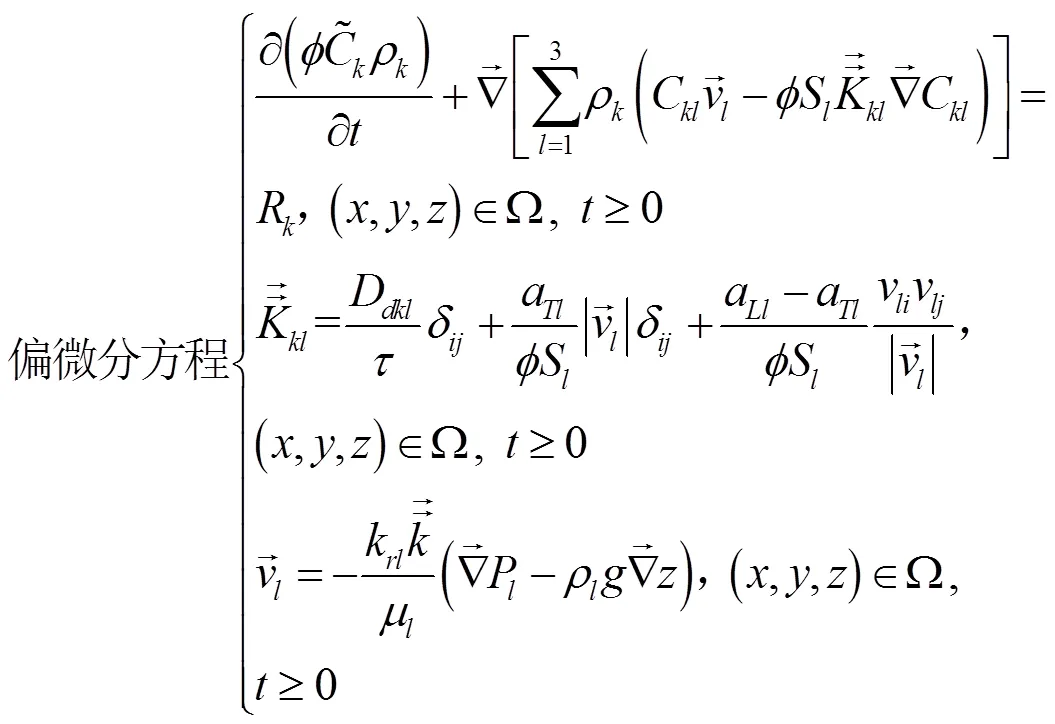
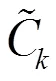
模型中的源汇项(污染源信息)是未知的,无法进行模型的校正及检验,使得模型中的含水层参数取值也无法确定.因此,该模型并不完整,是为进行地下水污染源反演识别而初步建立的.

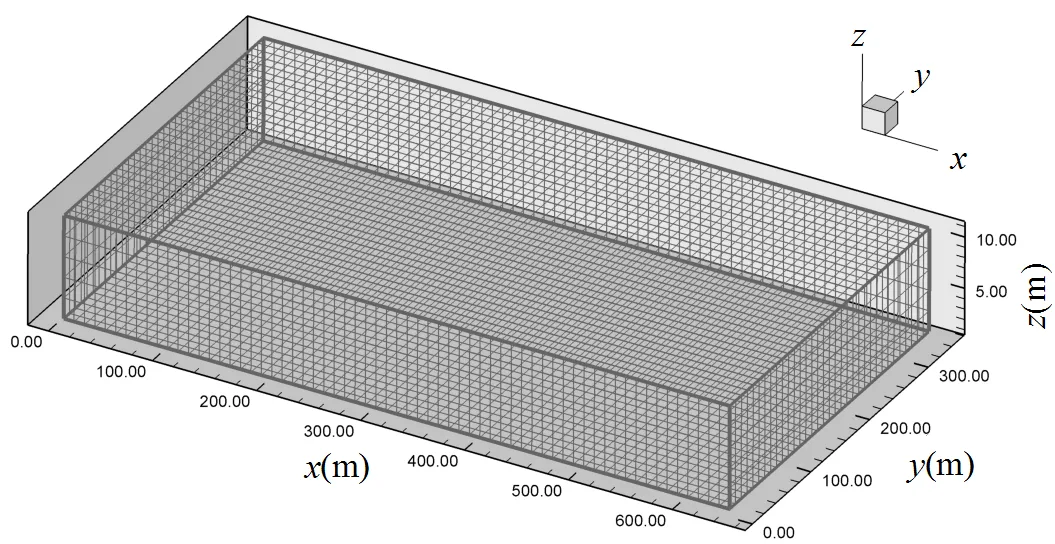
图2 计算区剖分示意

在后文的研究中,涉及到对污染源信息及含水层参数赋值并求解多相流模拟模型.进行多相流模拟模型的求解时,运用由美国德克萨斯大学研制的UTCHEM软件[25].研究区剖分图见图2.水质水位监测井的相对位置如图3所示.

2.3 替代模型的建立

通过敏感性分析(通过给定一个假想的污染源,运行多相流数值模拟模型实现)可知,孔隙度、渗透率、纵向水相弥散度、横向水相弥散度这4个参数的敏感度较高,而纵向油相弥散度、横向油相弥散度的敏感度几乎为零.因此,将孔隙度、渗透率、纵向水相弥散度、横向水相弥散度作为待识别参数,而将其他参数作为已知常数,根据经验在其取值范围内取值.

最终,本文污染源反演识别问题的待识别变量为:污染源的纵向坐标、污染源的横向坐标、污染物泄漏量、污染物迁移转化时长、孔隙度、渗透率、纵向水相弥散度、横向水相弥散度,共8个变量,各参数的初始估计范围是通过野外现场调研查和专家经验估计所得.以待识别变量作为优化的可控输入变量建立替代模型,替代模型的输出为末时刻三口监测井位置含水层底部的污染物浓度,即本文建立的核极限学习机替代模型有8个输入变量和3个输出变量.由于地下水污染物浓度的影响因素众多,因此,污染物浓度的监测值在一年内有剧烈的变化.本文将三口监测井中的含水层底部污染物浓度监测序列分别取平均值,近似表示各监测井位置末时刻含水层底部污染物浓度实际监测值.

本文设计的核极限学习机替代模型需要100个训练样品,20个检验样品.检验样本由不同于训练样本的样品点组成,用来检验替代模型对模拟模型的逼近精度.故需要进行2次拉丁超立方抽样,分别抽取训练样本和检验样本.抽样结束后,将样本方案多相流数值模拟模型,获得相应的输出(当前三口监测井位置含水层底部的污染物浓度).

替代模型训练样本数是根据替代模型输入输出的维度和经验确定.通过之前的研究经验发现,当替代模型的训练样本数量较少时,替代模型的精度会随着训练样本数量的增多而显著提高,而当训练样本数较多时,样本数量对替代模型精度的影响并不明显.训练样本的获取需要花费比较大的工作量,因此,通过权衡确定训练样本数为100.

根据核极限学习机方法的原理在MATLAB平台上编写程序,建立核极限学习机模型.运用100组训练样本对核极限学习机模型进行训练,将20组检验样本的输入数据输入训练好的核极限学习机模型,获得输出响应(污染物浓度数据),并将其与多相流模拟模型的输出响应对比.替代模型的输出变量为3个,由20组检验样本共可获得60个输出数据.在与与多相流模拟模型的输出响应对比后,可得到60个相对误差数据,相对误差(绝对值)的分布情况如图4、图5所示.结果表明:对于检验样本,替代模型的相对误差水平很低,绝大部分相对误差小于5%.

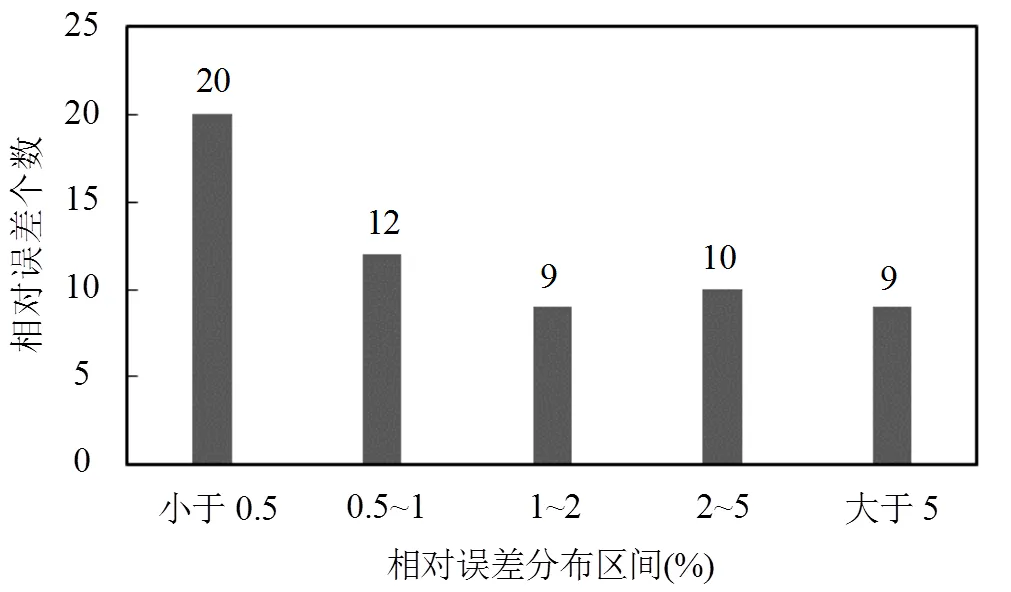
图4 替代模型相对误差分布

替代模型的各项精度评估指标如表2所示.核极限学习机模型的各项指标均比较优秀,即核极限学习机模型对模拟模型有较高的逼近精度,能够识别并取代模拟模型的输入-输出关系.综上,核极限学习机模型可以代替模拟模型与优化模型耦合进行污染源反演识别.

图5 替代模型相对误差频次累积曲线

表2 替代模型精度分析

2.4 优化模型的建立及求解

本文用以识别污染源和含水层参数的优化模型的目标函数可表示为:

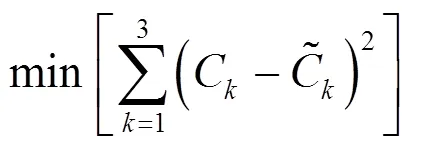
将目标函数与污染源相关变量约束以及含水层参数约束等约束条件组合,就构成了污染源反演识别的优化模型.在MATLAB平台上编写程序,应用基于模拟退火的粒子群优化算法对建立的非线性规划优化模型进行求解.通过不断更新粒子的飞行速度和位置,使粒子的适应度不断提高,最终得到满足所有约束条件的最优解.目标函数值收敛曲线如图6所示.优化求解过程中,在迭代进行到20次时,目标函数的种群最优值即达到了收敛,且目标函数值的下降幅度非常大.说明应用基于模拟退火的粒子群优化算法求解优化模型,能够以较快的速度搜寻到全局最优,且不依赖于初始值的选择.

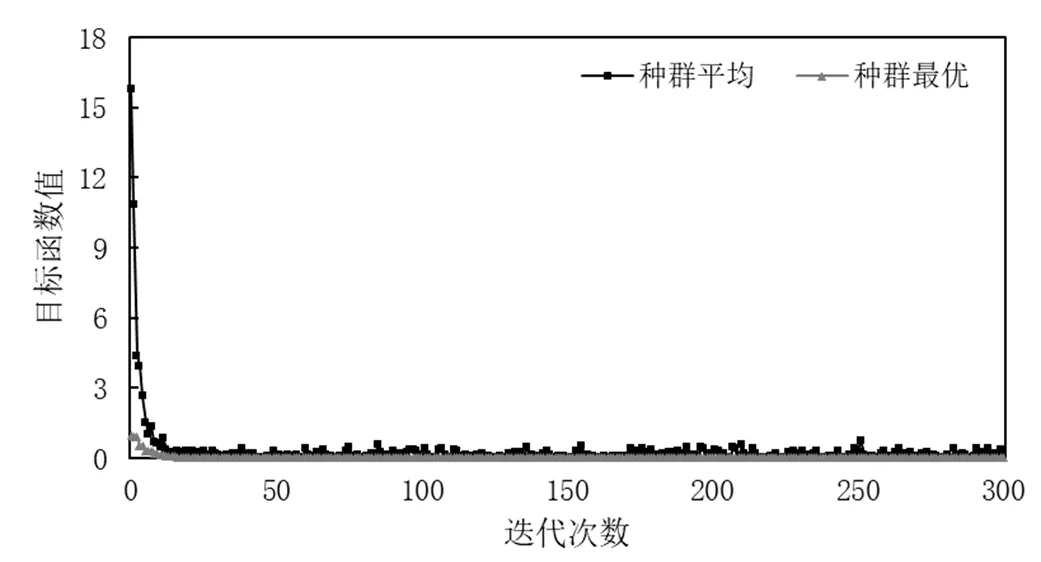
图6 优化识别过程中目标函数值收敛曲线

求解非线性优化模型获得的最优解即为污染源与含水层参数的识别结果,如表3所示,识别出的污染源位置见图7.根据污染源和含水层参数的识别结果重新建立研究区的多相流模拟模型,可以获得当前含水层中DNAPLs的分布状况,如图8所示.

图中污染物分布中心不在“S”点附近,是由于污染很可能是由一个爆炸事故引起的,污染物属于瞬时排放,而且根据识别结果,事故发生时间距今超过了十年,油相污染物全部溶于水中,污染中心会随着水流移动偏离污染源.识别出的污染源位置可以为污染责任认定提供可靠依据,而识别出的污染物分布情况对于修复方案设计和污染风险评价具有重要参考价值.

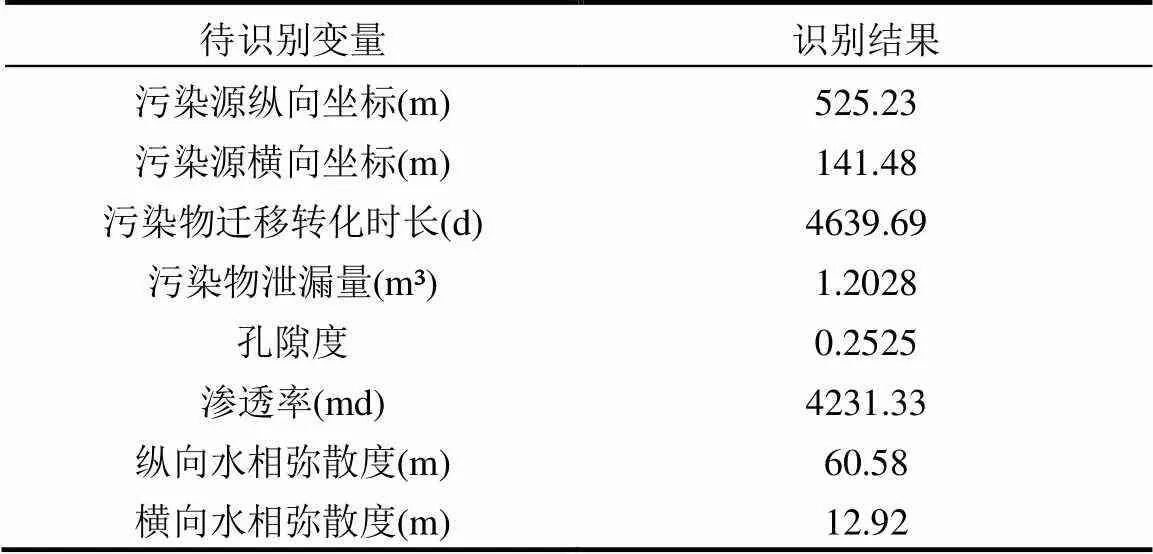
表3 污染源与含水层参数识别结果

模拟-优化方法的主要计算负荷来自于反复多次调用模拟模型.该硝基苯污染含水层多相流数值模拟模型在CPU为Intel core i5 3.0GHz内存为8GB的计算机上运行一次平均需要大约400s.如果用传统的模拟-优化方法来解决此问题,模拟模型需要运行18000(遗传算法初始种群数量为60,遗传代数为300)次,花费约83d时间.

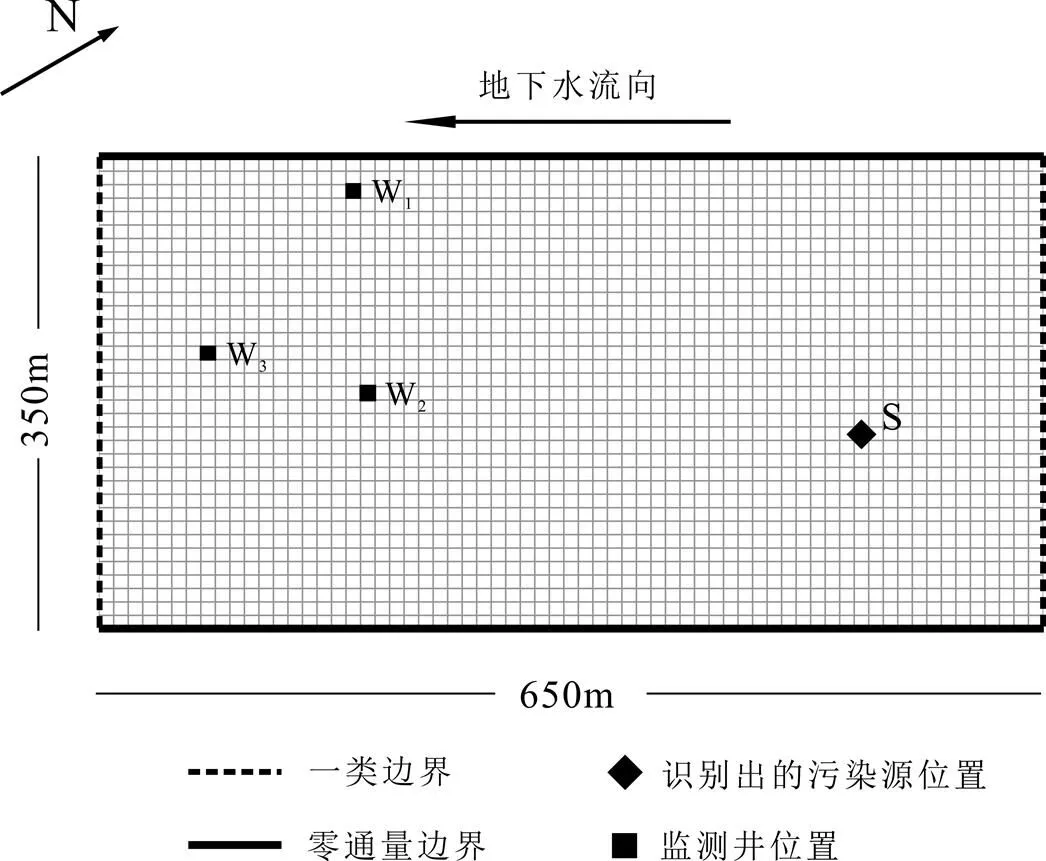
图7 污染源位置识别结果示意

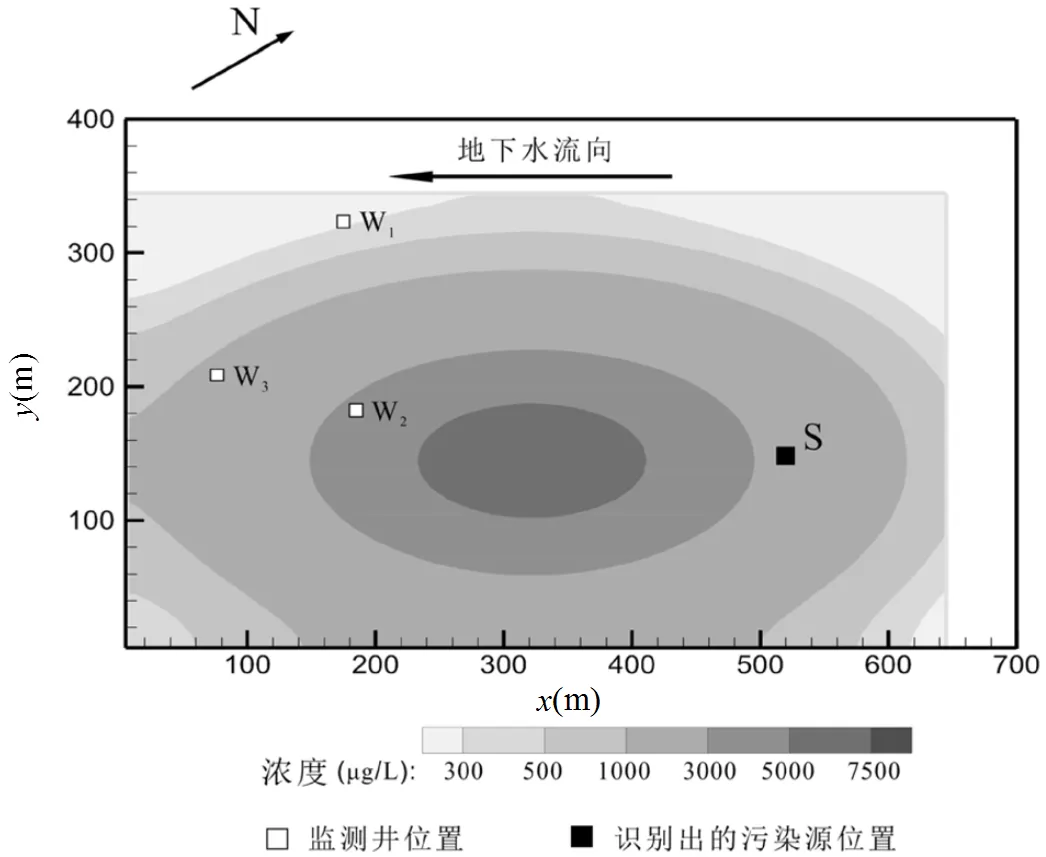
图8 污染物分布情况示意

核极限学习机模型运行一次需要0.8s,如果将核极限学习机模型引入模拟-优化模型中来代替模拟模型,优化求解过程只需要3h.因此,核极限学习机模型的引入在保证精度的同时大大减小了整个计算过程的计算负荷.

3 结论

3.1 核极限学习机替代模型对模拟模型有较高的逼近精度,能够识别并模仿模拟模型的输入-输出关系,绝大部分相对误差小于5%,平均相对误差仅有2.98%,可以代替模拟模型与优化模型耦合进行污染源反演识别.

3.2 应用基于模拟退火的粒子群优化算法可以高效地求解优化模型.优化求解过程中,在迭代进行到20次时,目标函数的种群最优值即达到了收敛,而且目标函数值的下降幅度非常大.说明应用基于模拟退火的粒子群优化算法求解优化模型,能够以较快的速度搜寻到全局最优,且不依赖于初始值的选择.

3.3 以替代模型代替模拟模型,大幅度地减小了模拟-优化过程的计算负荷,将反演识别时间由传统方法的83d减少到3h,并能够保持较高的计算精度.

3.4 应用基于替代模型的模拟-优化方法可以有效地完成地下水DNAPLs污染源与含水层参数的同步识别工作,为修复方案设计、污染风险评估和污染责任定提供可靠依据.

[1] Qin X S, Huang G H, He L. Simulation and optimization technologies for petroleum waste management and remediation process control [J]. Journal of Environmental Management, 2009,90(1): 54-76.

[2] Ayvaz M T. A linked simulation–optimization model for solving the unknown groundwater pollution source identification problems [J]. Journal of Contaminant Hydrology, 2010,117(1-4):46-59.

[3] 赵 莹.基于模拟-优化方法的地下水污染源反演识别[D]. 长春:吉林大学, 2017.Zhao Y. Inversion identification of groundwater pollution source based on simulation-optimization method [D]. Changchun: Jilin University, 2017.

[4] Sun N Z. Inverse problems in groundwater modeling [M]. Springer Netherlands, 2009.

[5] 张 宇.基于随机统计方法的地下水污染源反演识别研究 [D]. 长春:吉林大学, 2016.Zhang Y. Inversion recognition of groundwater pollution source based on stochastic statistical method [D]. Changchun: Jilin University, 2016.

[6] Mahinthakumar G K, Sayeed M. Hybrid genetic algorithm – Local search methods for solving groundwater source identification inverse problems [J]. Journal of Water Resources Planning and Management, 2005,131(1):45–57.

[7] Liu X, Cardiff M A, Kitanidis P K. Parameter estimation in nonlinear environmental problems [J]. Stochastic Environmental Research and Risk Assessment, 2010,24(7):1003–1022.

[8] Wang H, Jin X. Characterization of groundwater contaminant source using Bayesian method [J]. Stochastic Environmental Research and Risk Assessment, 2013,27(4):867-876.

[9] Gurarslan G, Karahan H. Solving inverse problems of groundwater- pollution-source identification using a differential evolution algorithm [J]. Hydrogeology Journal, 2015,23(6):1109-1119.

[10] 顾文龙.基于MCMC方法的地下水污染源反演识别[D]. 长春:吉林大学, 2017.Gu W L. Inversion identification of groundwater pollution source based on MCMC method [D]. Changchun: Jilin University, 2017.

[11] Srivastava D, Singh R M. Breakthrough curves characterization and identification of an unknown pollution source in groundwater system using an artificial neural network (ANN) [J]. Environmental Forensics, 2014,15(2):175-189.

[12] Zhao Y, Lu W X, Xiao C N. A Kriging surrogate model coupled in simulation-optimization approach for identifying release history of groundwater sources [J]. Journal of Contaminant Hydrology, 2016,185: 51-60.

[13] 肖传宁.地下水污染源反演识别研究[D]. 长春:吉林大学, 2017.Xiao C N. Inversion identification of groundwater pollution sources [D]. Changchun: Jilin University, 2017.

[14] 李守巨,刘迎曦.基于蚁群算法的地下水污染源辨识方法[J]. 计算机科学, 2005,32(8):289-291.Li S J, Liu Y X. Groundwater pollution source identification method based on ant colony algorithm [J]. Computer Science, 2005,32(8):289- 291.

[15] 江思珉,张亚力,蔡 奕,等.单纯形模拟退火算法反演地下水污染源强度[J]. 同济大学学报(自然科学版), 2013,41(2):253-257.Jiang S M, Zhang Y L, Xai Y. Inversion of groundwater pollution source intensity by simplex simulated annealing algorithm [J]. Journal of Tongji University (Natural Science Edition), 2013,41(2):253-257.

[16] Jha M, Datta B. Application of dedicated monitoring-network design for unknown pollutant-source identification based on dynamic time warping [J]. Journal of Water Resources Planning and Management, 2015,141(11):04015022.

[17] 肖传宁,卢文喜,安永凯,等.基于两种耦合方法的模拟-优化模型在地下水污染源识别中的对比[J]. 中国环境科学, 2015,35(8):2393- 2399.Xiao C N, Lu W X, An Y K, et al. Comparison of simulation- optimization models based on two coupling methods in the identification of groundwater pollution sources [J]. China Environmental Science, 2015,35(8):2393-2399.

[18] 李敏强,寇纪淞,林 丹,等.遗传算法的基本理论与应用[M]. 北京:科学出版社, 2002:63-65.Li M Q, Kou J S, Lin D. The basic theory and application of genetic algorithm [M]. Beijing: Science Press, 2002:63-65.

[19] 余 丽.地理网络中求解TSP的并行混合算法研究[D]. 北京:中国地质大学, 2013. Yu L. Research on Parallel Hybrid Algorithm for Solving TSP in Geographical Network [D]. Beijing: China Geosciences University, 2013.

[20] Sreekanth J, Datta B. Multi-objective management of saltwater intrusion in coastal aquifers using genetic programming and modular neural network based surrogate models [J]. Journal of Hydrology, 2010,393(3/4):245–256.

[21] Yao W, Chen X, Huang Y, et al. A surrogate-based optimization method with RBF neural network enhanced by linear interpolation and hybrid infill strategy [J]. Optimization Methods and Software, 2014, 29(2):406-429.

[22] 姜 雪.DNAPLs污染含水层修复方案优选及不确定性分析[D]. 长春:吉林大学, 2016.Jiang X. Optimization and uncertainty analysis of DNAPLs contaminated aquifer repair scheme [D]. Changchun: Jilin University, 2016.

[23] Manoochehri M, Kolahan F. Integration of artificial neural network and simulated annealing algorithm to optimize deep drawing process [J]. International Journal of Advanced Manufacturing Technology, 2014,73(1-4):241-249.

[24] 侯泽宇.基于替代模型的DNAPLs污染含水层修复方案优选过程的不确定性分析[D]. 长春:吉林大学, 2015. Hou Z Y. Uncertainty analysis of optimization process of DNAPLs contaminated aquifer restoration scheme based on surrogate model [D]. Changchun: Jilin University, 2015.

[25] Delshad M, Pope G A, Sepehrnoori K. A compositional simulator for modeling surfactant enhanced aquifer remediation, 1. formulation [J]. Journal of Contaminant Hydrology, 1996,23(4):303–327.

Surrogate-based source identification of DNAPLs-contaminated groundwater.

HOU Ze-yu1,2, LU Wen-xi1,2*, WANG Yu1,2

(1.Key Laboratory of Groundwater Resources and Environment Ministry of Education, Jilin University, Changchun 130021, China；2.College of Environment and Resources, Jilin University, Changchun 130021, China)., 2019,39(1)：188~195

Groundwater contamination source identification (GCSI) is critical for taking effective actions in designing remediation strategies, estimating risks, and confirming responsibility. Surrogate-based simulation-optimization technique was applied to source identification and parameter estimation of DNAPLs-contaminated aquifer in this article. The results showed that: 1) kernel extreme learning machines (KELM) surrogate model approximated the simulation model accurately. It could simulate the input/output relationship of the simulation model with most of the relative errors less than 5%, and the mean relative error was only 2.98%; 2) Replacing the simulation model with a KELM model considerably reduced the computational burden of the simulation-optimization process and maintained high computation accuracy, the identification time was reduced to 3hours from 83days; 3)Simulated annealing-based particle swarm optimization algorithm is efficient in searching the global optimal solution of the nonlinear programming optimization model, and avoiding the optimization process trapping into local optimum.

Dense non-aqueous phase liquids (DNAPLs)；contamination source identification；simulation-optimization；multi-phase flow simulation；KELM surrogate model

X523

A

1000-6923(2019)01-0188-08

侯泽宇(1989-),男,河北唐山人,博士后,主要从事地下水污染控制与修复研究.发表论文20余篇.

2018-06-04

国家自然科学基金项目(41672232);吉林省科技发展计划项目(20170101066JC)

* 责任作者, 教授, luwx999@163.com