从情境出发 让数学生活化
——《百分数的意义》教学设计
2019-02-11江苏省淮安市淮阴师院附小张海艳
江苏省淮安市淮阴师院附小 张海艳
【教学内容】苏教版六年级上册教材第六单元第一课时84~85页
【教学过程】
一、创设情境,初步感知
谈话:同学们,足球活动是我们学校的特色,近年来我们学校以足球活动为平台,形成了浓厚的校园文化特色,足球运动增强了学生的体质,树立了他们的团队意识,为学生营造了一个健康、快乐的校园文化氛围。
看这是我校三位同学的射门情况。

姓名 射球次数 射中次数1号 10 6 2号 10 8 3号 10 7
从表中你能快速判断出哪位同学射门技术高吗?
独立思考,汇报。
生1:他们射门次数一样,我们就看射中次数就可以,所以2号射门技术好。
生2:他们射门次数相同,也可以看他们没有射中的次数,丢球少的同学是2号,所以他射门技术高。
生3:射门次数与射中次数的比。第一位是 10∶6=5∶3,第二位是 10∶8=5∶4,第三位是10∶7。这样比较发现2号球员射门技术高。
同学们,刚刚我们通过思考,比较几种方法,都认为通过比较他们射中次数占射门次数的比来比较出谁的射门技术高,这一方法比较科学合理。
二、合作探究、感知概念
第九届足球文化节又要开始招募队员了,老师想从我们班选一位同学参加比赛,他们三位同学的射门情况统计如下:

images/BZ_54_330_2691_793_2915.png
你还能一眼就判断出哪位同学射门技术高吗?请独立思考,把思考过程完成在学习单上。
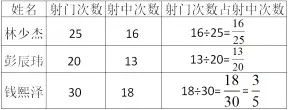
你现在可以判断出哪位同学射门技术高了吗?你有什么好办法解决这个问题呢?
(实际情境中引入课题,让学生参与经历数学知识的呈现过程,了解知识产生的背景。)
独立思考,汇报:
生 1:化成小数:16/25=0.64,13/20=0.65,3/5=0.6,因为 0.65>0.64>0.60,所以彭辰玮的射门技术高。
生 2:我是找 25、20、5 的最小公倍数是 100,16/25=64/100,13/20=65/100,3/5=60/100,65/100>64/100>60/100,所以 2 号彭辰玮射门技术高。
师:为什么要化成分母100?
生齐答:可以快速看出大小。
老师还带来了几组数据,你能帮老师快速判断吗?小组合作完成。
A.哪杯糖水更甜?学习百分数的热情做铺垫 。学生自己积极参与到百分数意义的形成过程中,体会百分数在统计和比较中的优势。)
请观察这几组数据,屏幕出现通分的过程,让学生感知通分的优势。
最左面这列数都有什么特点?预设:(分母都是100)
它们都表示的是几个量之间的关系?(两个量的关系)

B.哪种种子的发芽率高?

小组汇报计算比较结果:
第一题:1号杯糖占糖水 27÷50=27/50=54/100,2号杯糖占糖水 11÷20=11/20=55/100,所以2号杯糖水更甜。
第二题:A种子发芽种子数占种子总数 178÷200=178/200=89/100,B 种子的发芽种子数占是93÷100=93/100,所以B类型种子的发芽率高。
(设计意图:不同的生活实例计算发现,分母100时更便于比较大小,为激发
三、合作交流,理解概念
1.揭示概念
像这样表示一个数是另一个数百分之几的数就叫百分数,也叫百分率或百分比。(板书概念)
追问:百分数能带单位吗?
生:它表示的是一种倍比关系,不能加单位。
2.百分数读写教学
生产、生活中为了便于统计和比较,像上面这样的数,还有更简洁的写法。
64/100=64%。读作:百分之六十四。
65/100= 60/100=
让学生继续改写作业单上的百分数,注意百分号的书写,圆圈要写的小点,避免与零混淆。
3.理解百分数意义。
提问:64%、65%、60%表示的是什么意思呢?
预设:64%表示的是:林少杰同学射中次数占射门次数的64%。65%表示的是彭辰玮同学射中次数占射门次数的65%,60%表示的是钱熙泽射中次数占射门次数的60%。
追问:这些百分数都表示的是什么?
(设计意图:把百分数的意义的知识镶嵌在真实的问题情境中,激发学生学习的需要和高层次的思考,从而自觉地参与到学习的过程中来。)
预设:一个量占另一个量的百分之几。
谈话总结:表示一个量是另一个量百分之几,就是今天研究的百分数的意义。
四、引导建构,理解概念
1.比较分数与百分数的异同?
小组交流、汇报
生1:读法、写法不同。
生2:分子不同,分数分子只有整数,而百分数的分子可以是整数,也可以是小数。
生3:意义不同,百分数只能表示分率,而分数可以表示具体的量,可以带单位。
2.生活中的百分数,进一步理解百分率与百分比。
同学们展示课前收集的材料,小组内说说百分数的意义。
老师通过课件出示收集的百分数。
(1)六年级学生的近视率是18.4%。
18.4%表示的是什么?近视率会超过100%吗?
谈话:百分数可以表示分率,又叫百分率。
(2)一艘轮船货物装了75%。已装货物与货物总量的比是( ):100,百分数也可以表示后项是100的比,也叫百分比。
(3)我们班男生人数是女生人数的160%。说说160%的意义。
追问:什么情况下,百分数可能大于1?什么时候不能大于1?小组讨论,汇报。
总结:当表示部分与整体关系的时候百分数不能大于1,当表示部分与部分关系时候可以大于1。
五、练习中提升
1.哪些数可以改写成百分数?
(1)一根钢管长 95/100米,用去它的30/100。
(2)40/100千克是80/100千克的50/100。
(3)母鸡的只数是公鸡只数的115/100。
(4)一支铅笔的价格是120/100元,降价后现价是原价的90/100。
预设:30/100可以用百分数表示,它表示的是两个量之间的关系。
(设计意图:通过练习使学生体会百分数的本质是表示两个数量的倍比关系,不能表示具体的量。正确区分百分数与分数的区别与联系。)
2.根据百分数的意义填空
(1)新区学校有5%的同学参加了航模社团,航模人数是全校人数的( )∶100,航模人数与全校人数的比是( )∶100。
(2)电机厂实际生产电机的台数相当于原计划的120%。
( )是( )的120%。
(设计意图:根据百分数意义的理解,启发体会百分数与分数、比之间的联系,以进一步丰富对百分数意义的感知。)
六、总结延伸,深化意义
总结收获:
1.今天你学到了什么?
2.你收获了( )% 。
畅谈本节课的收获。用百分数表示学生自己的收获,不足的地方课后改进!
