基于DDPG的仿人形机器人仿真研究

(西华师范大学电子信息工程学院 四川 南充 637000)

一、前言

人形机器人步态控制是验证各种机器学习算法的有效平台，在现有各种机器学习算法中，为实现人形机器人学会稳定行走，基于强化学习的步态控制算法取得了突破性成功[1]。通过强化学习的思想，让人形机器人行走时连续的感知周围环境，根据当前状态选择最优动作，最终训练出能使机器人稳定行走的模型。Timothy等人提出的深度确定性策略梯度算法(DDPG，Deep Deterministic Policy Gradient)取得不错的效果[2]。本文通过BipedalWalker-v2仿真环境验证该算法，并对提高环境探索能力的正态分布噪声的参数进行分析。

二、DDPG算法

DDPG结合DQN(Deep Q-Learning)算法中得缓冲回放模型和目标网络结构，缓冲回放将一些采样样本收集起来，每次优化时从中随机取出一部分进行优化，从而减少一些不稳定性。目标网络结构使计算目标价值的模型在一段时间内被固定，从而减少模型的波动性。融合Actor-Critic算法的框架，建立Actor和Critic网络，Actor网络用于与环境交互，并产生当前策略，Critic网络用来评估当前策略。以及DPG(Deterministic Policy Gradient)算法的结论，可以用一个值函数模型来拟合目标函数中得价值估计部分[3]。为提高对环境的探索能力，动作选取公式如式(1)，N为正态分布噪声。

(1)

DDPG算法流程如下：

首先初始化Actor网络参数θ、θ’，Critic网络参数ω、ω’，以及经验回放D，令ω'=ω,θ'=θ。

对每一个回合，循环以下步骤：

(1)初始化S为当前状态序列的第一个状态S，拿到其特征向量φ(S)；

(2)在Actor当前网络基于状态S得到A=πθ(φ(S))+Ν；

(3)执行动作A，得到新状态S'，奖励R，判断是否终止状态，未终止，执行(4)；

(4)将{φ((S),A,R,φ((S'),is_end}存入在经验回放集合D中；

(5)从经验回放D中均匀采样m个样本{φ((Sj),Aj,Rj,φ((S'j),is_endj},j=1,2,…,m,并计算当前目标Q值yj：

yj=rj+γQ'(φ(S'j),πθ'(S'j),ω')

(2)

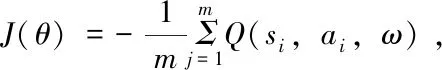
(8)更新目标网络参数：

θ'←τθ+(1-τ)θ'

(3)

ω'←τω+(1-τ)ω'

(4)

(9)如果S'是终止状态，当前轮迭代完毕，否则转到步骤(2)。

三、实验数据与分析

本次研究仿真部分，使用ubuntu16.04操作系统和Sublime代码编辑器，仿真环境是OpenAI的Gym环境，深度学习框架是TensorFlow。

(一)BipedalWalker-v2仿真环境

在Gym提供的BipedalWalker-v2环境中，机器人通过调整到比较好的姿态获得更高的分数。通过读取场景的信息，环境状态输入部分有24个值，包括角速度，水平速度，垂直速度，关节位置，关节角速度，腿与地方接触的位置，以及10个激光雷达测距仪测量等。每个值得范围都是从负无穷到正无穷，反馈输出的动作有4个值，每个值的范围都是从-1到1，环境信息如表1所示[4]。

表1 BipedalWalker-v2的信息

(二)仿真结果

1.算法有效性

在BipedalWalker-v2环境中的学习效果如图1所示，正态分布中标准差最大值为4，最小值为0.001，经过1000轮的学习。可以取得较好的学习效果。

图1 BipedalWalker-v2仿真结果

2.数据分析

当标准差最大值一定时，改变标准差最小值，仿真结果如图2所示。当标准差初始值为4时，分别设定标准差最小值为0.01、0.001和0.0001，从图中可以看到随着训练次数的增加，奖励最后趋于稳定，当标准差最小值为0.01时，在训练回合到3000时还是会有较大的波动，奖励值没有很好的收敛。标准差最小值为0.0001时，奖励值虽然可以收敛，但是收敛值保持在30左右，没有获得较好的分数。标准差的值为0.001时，奖励值不仅可以收敛还能够保持较高的分数。这种现象说明，随着训练次数的增加，机器人可以逐渐得到较高的奖励，但是在已经得到高奖励的情况下，还是以较大的标准差来处理动作值，就会带来较大的波动，同时若标准差的最小值设置过小，机器人在开始的学习中容易因为探索不够，会需要更多的学习回合才能获得较好的奖励值。在训练过程中，随着训练次数的增加，后期所用的都是标准差最小值，并且因为其奖励随训练回合数的曲线变化是呈锯齿状的，若标准差最小值过小，就很可能出现收敛在较小奖励值的情况。

图2 scale=4仿真结果

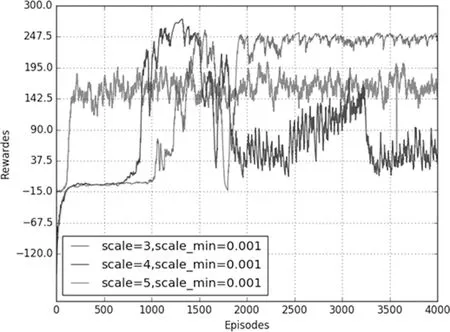
图3 scale_min=0.001仿真图

当标准差最小值一定时，改变标准差最大值，仿真结果如图3所示。从图中可以看到，当标准差初始值分别为3，4，5时，随着训练次数的增加最后都可以收敛，但是它们最后的收敛值来看，标准差初始值为3时收敛值最小，标准差初始化值为4时收敛值在240左右，初始值为5时的收敛值在230左右，并且标准差为4时奖励最大值相较其他两种最大。标准差初始值主要是为了在开始训练的一段时间给机器人较大的动作选择自由，能够进行充分的探索，通过尝试得到获取高奖励的经验，为后期的训练积累到好的学习经验。初始值过小会使得机器人还未能有一定的好的学习经验，但是随着训练回合数的增加，给予机器人的自由会逐渐减少至0.001，从而导致它将很难再学习到更好的结果。初始值设置过大，即给予机器人的自由度过大，甚至远远超过DDPG模型中原本的动作选取策略，显然会使DDPG模型的训练效果大打折扣。

从仿真结果可以得出标准差的最小值在很大程度上影响奖励是否收敛，标准差的初始值会影响收敛值的大小，它们都是DDPG模型的关键参数。调整好这两个参数的大小，会决定是否能得到好的训练结果。

四、结束语

本文将深度确定性策略梯度算法用于人形机器人的步态研究，在BipedalWalker-v2环境中验证该算法的可行性，验证中发现该算法中，提高对环境探索能力的正态分布参数对于学习效果的影响很大，分别讨论正态分布中的标准差和最小标准差对学习效果的影响，以及Batch Size的大小对于学习效果的影响，具有一定的参考意义。