一道经典力学题的解析探讨
2019-02-10葛水兵
葛水兵
(苏州大学物理科学与技术学院,江苏 苏州 215006)
物理教学中,精选例题,一题多解,可以加深学生对基本概念、基本原理的理解和应用.本文精选了一道力学例题,采用 “微元法”、“微积分法”和“函数图像法”3种方法进行解题.并通过问题的拓展,探求解决问题的思路,旨在培养学生创造性思维能力.
1 一道经典题目
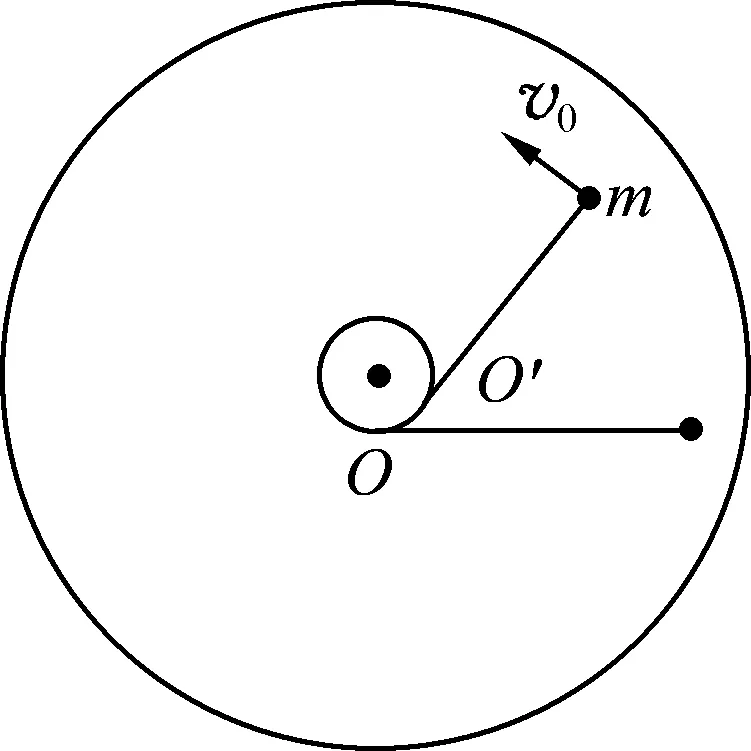
图1
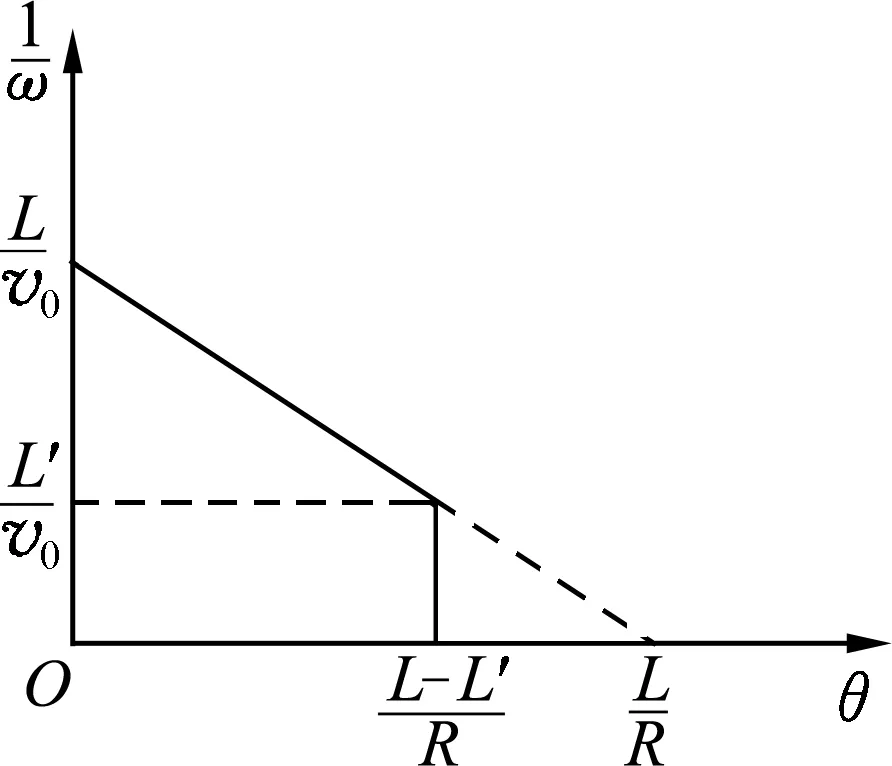
例题.在光滑水平圆桌面的圆心处立着一根半径为R的竖直圆柱子,如图1所示,一根不可伸长的柔软细轻绳,一端固定在立柱下部一点上,另一端系一质量为m的小球.将小球放在桌面上并把绳拉直,绳伸直部分的长度为L.现给小球一个方向与绳垂直、大小为v0的初速度.小球在桌面上运动时,绳将缠绕在立柱上,忽略摩擦.已知当绳的张力为T0时,细绳即断开.设初始时,绳中的张力为T (1) 计算经过多少时间细绳断开,首先要计算细绳断开瞬间,细绳伸直部分的长度. 要求细绳伸直部分的长度,需要分析小球的运动过程.有些学生分析后得出结论:小球作螺旋线运动,因为细绳伸直部分的长度逐渐减小,绳的拉力做正功,小球的速度增大.这个结论正确吗?不正确.为什么呢?这些学生只看到了小球运动的表面现象,并没有发现本质问题.例题已知条件表明:桌面是光滑的,小球初速度方向与绳垂直,细轻绳不可伸长,且在断开前细绳一直是绷紧的.所以在绳断开前,小球在沿桌面运动的过程中,其速度方向始终与绳垂直.假设不垂直,那么在沿绳方向必然存在速度分量,因为细绳一端固定在圆柱上,所以细绳不可能一直被拉紧,与题中的情形相矛盾. 基于以上分析可知:在绳断开前,小球在沿桌面运动的过程中,其速度方向始终与绳垂直,绳子的张力对小球不做功,小球速度大小保持不变.[1,2]任意时刻,小球的运动可看作以细绳与圆柱的切点为瞬时圆心,以未缠绕的细绳为半径的圆周运动. 设在细绳断开瞬间伸直部分的长度为L′,细绳的拉力只提供小球的法向加速度,有 (1) 所以 (2) (2) 计算细绳伸直部分的长度从L缩短至L′所经历的时间. ① 解法1(微元法). 因为细绳断开瞬间伸直部分的长度为L′,则缠绕在圆柱上的长度为L-L′.令 (3) 设细绳依次缠绕Δx所需的时间分别为Δt1,Δt2,…,Δtn,有 (4) (5) (6) 类推可得 (7) 联立(4)-(7)式,得 (8) 将(3)式代入(8)式,整理可得 (9) 当n→∞时,(9)式变为 (10) ② 解法2(微积分法). 设经过一定时间后,绳与圆柱的切点绕圆柱的圆心转过了θ角,即有Rθ长的绳绕在柱子上了,此时小球做圆周运动的半径变为L-Rθ,则小球运动的角速度为 (11) (12) 联立(11)和(12)式,有 (13) (13)式变形,有 (14) (14)式两边积分,得 (15) 图2 ③ 解法3(函数图像法). 分析小球的运动过程(同解法2)可知,细绳断开前的任意瞬间,小球运动的角速度为 (16) (16)式两边取倒数,得 (17) (18) 综合上述3种解题方法可知: (1) 微元法是从部分到整体的思维方法,把一些复杂物理过程简单化.微元法处理问题时,将整个过程分解为许多微小的“元过程”,先通过分析一个“元过程”,再将“元过程”进行必要的数学方法处理,从而解决整个过程问题.微元法是微积分法的萌芽,是高中阶段用来分析、解决类似物理问题的常用方法.(2) 微积分是高等数学中研究函数的微分、积分以及有关概念和应用的数学分支.微积分使函数可用一套通用的符号进行讨论,为定义和、求和提供了一套通用的方法,从而简化繁琐的数学运算,是大学阶段解决物理问题的常规方法.(3) 函数图像法简单明了,具有一定的技巧性.该方法解题时,必须熟悉坐标横轴、纵轴代表的物理量及其函数关系;熟悉函数图像的规律,预判函数图像形状的规则性;熟悉函数图线与坐标横轴、纵轴所围面积的物理含义.图像法提供了更加快捷的解题思路,将数学和物理有机地结合起来,是一种行之有效的解题方法.全面理解物理图像的意义,熟练应用图像处理物理问题,是物理教学中必备的基本技能. (1) 细绳全部缠绕. 由(10)、(15)、(18)式可知,细绳全部缠绕在立柱上的时间,只需代入L′=0即可求出一致的结果.[2]然而细绳全部缠绕需要进一步探讨,根据(2)式可知,要L′=0,细绳承受的张力必须无穷大.显然这与现实生活中的情形相悖,难以理解.因为细绳或细线承受的张力有限,所以全部缠绕问题是本文例题的一个理想化特例.因而本文精选的例题更具典型性和代表性,在教学中更具说服力. (2) “一题多解” 可以培养学生的创造性思维能力;“一题多变”也可以培养学生的发散思维能力. 例题中如果已知圆桌面的半径及高度,则可以计算细绳断开后,小球在地面的落点与桌面圆心的水平距离.此题的拓展将涉及到平抛运动,由于解题思路比较清晰,过程也比较简单,在此不再详述,读者可自行解题.2 多种解题方法
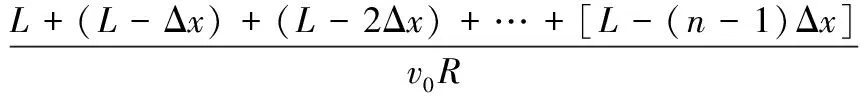
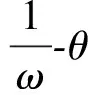
3 拓展
