运用导数和积分数学方法正确解读运动图像问题

郭清鹏

(山东省青岛第九中学,山东 青岛 266000)

目前,高考物理重点考查的5大能力包括:理解能力、推理能力、分析综合能力、应用数学处理物理问题的能力、实验能力．关于“应用数学处理物理问题的能力”《考试说明》是这样叙述的:能够根据具体问题列出物理量之间的关系式,进行推导和求解,并根据结果得出物理结论;能运用几何图形、函数图像进行表达、分析.可见,学生能运用数学知识解决物理图像问题,是一项必备能力．

物理图像是物理规律的一种数学呈现方式,只有准确解读物理图像中的信息才能正确分析和把握物理规律,高中数学的微积分知识为正确解读高中物理图像问题提供了工具．物理学与数学有着密切的关系,诺贝尔奖得主、著名华裔物理学家杨振宁先生将数学与物理的关系比做“双叶”,他认为数学和物理学像一对“对生”的树叶,他们只在基部有很小的公共部分,多数则是相互分离的．他这样解释 “物理与数学,有各自不同的目标和价值判断准则,也有不同的传统,在它们的基础概念部分令人吃惊地分享着若干共同的概念”．正是数学和物理相交叉的公共部分,为物理学的发展提供了强有力的工具,其中数学中的导数和积分概念就自带“数理结合”的基因．导数的本质是通过极限的概念对函数进行局部的线性逼近,在运动学中物体的位移对于时间的导数就是物体的瞬时速度,物体的速度对于时间的导数就是物体的加速度．在数学上,对任意一个函数求其在某一可积分区间内与x轴所围成的面积的操作就是积分,积分应用于物理学则是求解一个物理量对另一个物理量的累积效果．运动图像中“面积”就可以表示纵坐标对应物理量在横轴对应物理量上的积累,譬如,(瞬时)速度-时间图像中的“面积”表示位移．

高中物理运动图像中的信息大致可以分为“直接信息”和“间接信息”．“直接信息”是可以通过横、纵坐标直接判断物理量之间关系的信息,譬如位移-时间图中的某时刻的位移,速度-时间图像中的某时刻的速度等．“间接信息”则是对物理规律的函数解析式进行数学处理后,得到的物理信息,譬如位移-时间图中的速度信息;速度-时间图像中加速度、位移等信息;加速度-时间图像中的速度变化量信息等．这些信息用数学中的“导数”和“积分”可以很方便地得到,使得某些重要物理量以精确的数学量呈现出来,从而提升解题的准确性和便捷性．

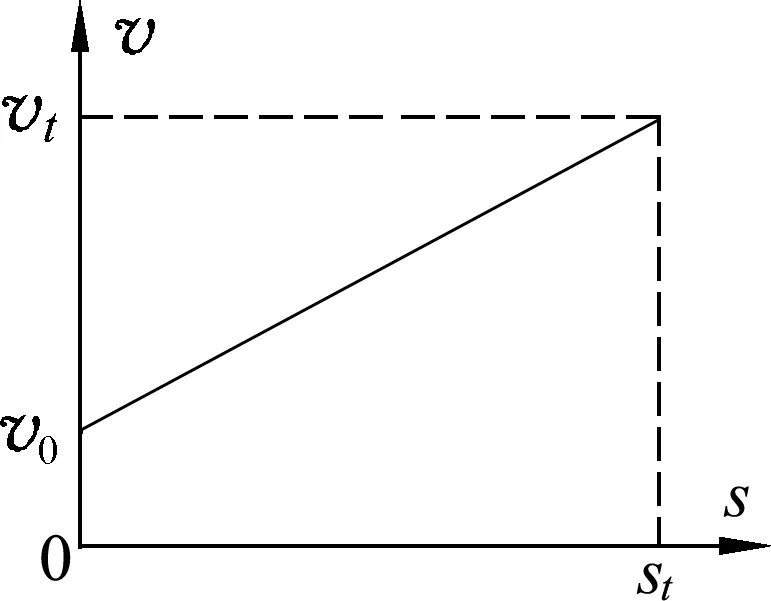
图1

例1.一质点沿直线运动,其速度-位移图像为一条如图1所示的直线.下列说法中正确的是

(A) 加速度增大.

(B) 加速度不变.

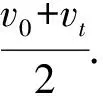
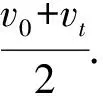
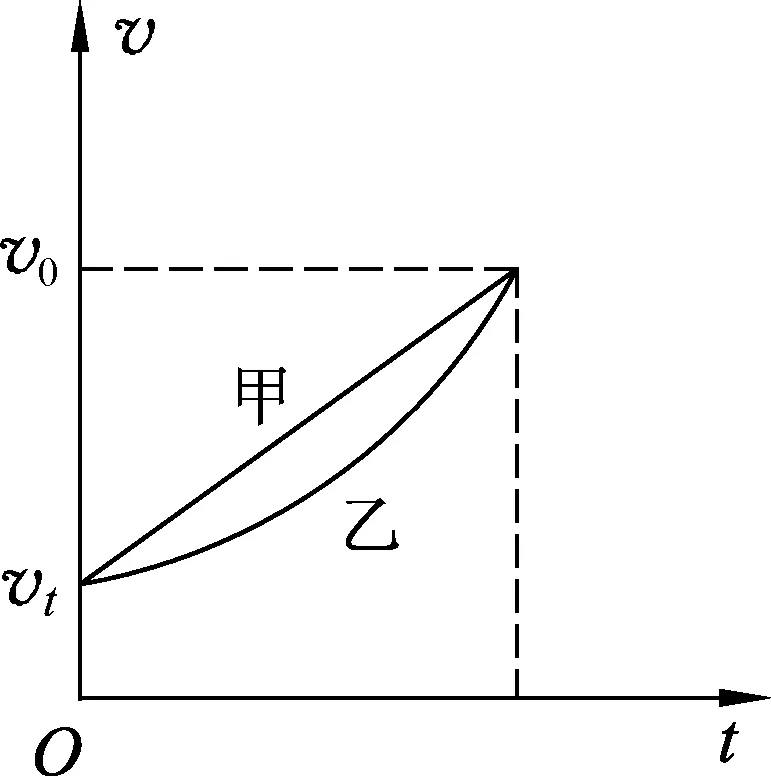
图2

解析.此题所给图像不是常见的速度-时间图像,单纯从物理角度很难与常见的物理情景对应,需要借助导数和积分处理图像所描述的物理量间的关系.然后,才能进一步分析数学处理结果的物理意义．首先,写出速度-位移图像的数学解析式为v=v0+ks,其中k为图线斜率,将该式两边对时间t求导,可得a=kv,可见,加速度与速度成正比,加速度随速度增加而变大,(A)选项正确．其次,根据加速度、速度都随时间变大这一事实,定性作出如图2速度-时间关系图像,其中甲为匀变速直线运动的速度-时间图像,乙为本题物体运动的速度-时间图像．最后,根据速度-时间图像中图线所围成的“面积”对应位移,相同时间内,当曲线与横轴所围面积为st时,斜线与横轴所围成的面积大于st,所以,匀变速直线运动的平均速度大于加速度逐渐增大的直线运动的平均速度,(C)、(D)选项均错误．

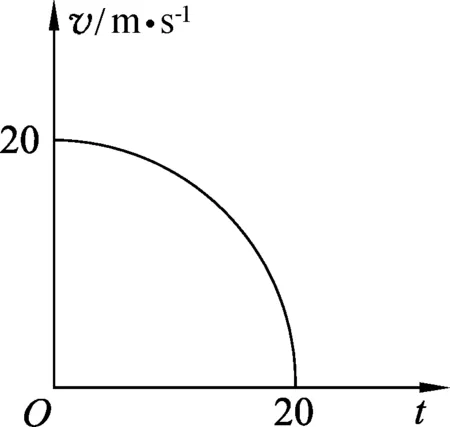
图3

例2.一物体做直线运动的v-t图像如图3所示,图线为1/4圆弧,则下列说法正确的是

(A) 物体做匀减速直线运动.

(B) 物体在10 s末的速度为15 m/s.

(C) 物体在20 s内速度的平均速度为10 m/s.

解析：此题所给出的图像虽是v-t图像,但不是直线图像,由数学知识解读速度与时间关系,可知速度与时间应满足圆的标准方程:

v2+t2=202.

(1)

首先,将其变形为

(2)

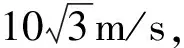
例3.已知一质点做变加速直线运动,初速度为v0,其加速度随位移线性减小的关系即加速过程中加速度与位移之间的关系满足条件a=a0-ks,式中a为任一位置处的加速度,s为同一位置时的位移,a0、k为常量,求当位移为s0时质点的瞬时速度．

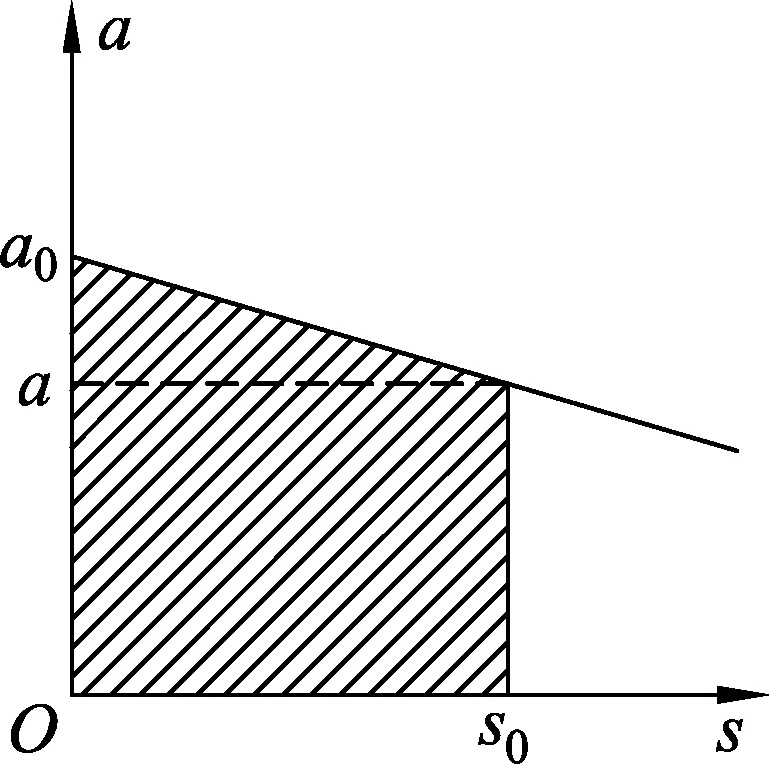
图4

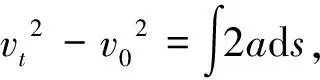
2a0s0-ks02,

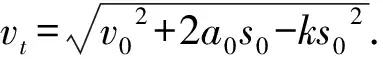
由以上例题可见,由运动图像写出物体运动规律的函数解析式,并对函数解析式进行求导和积分操作,利用“斜率”、“面积”与相关物理量之间的对应关系,是有效解决运动学的图像问题的重要方法．

值得注意的是,学生在应用“导数”和“积分”解决运动学图像问题时,经常会出现“数”“理”两张皮的情况．

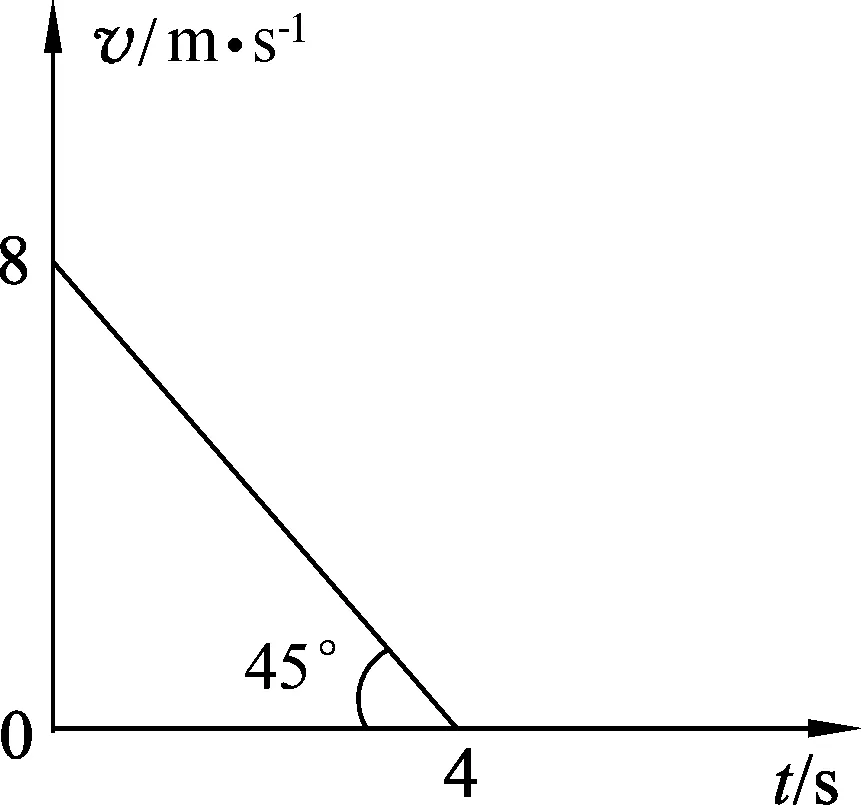
图5

例4.一个物体做匀变速直线运动的v-t图像,如图5所示,试求其加速度.

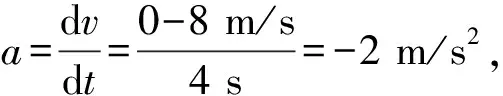
要解决像这种运用“数理结合”思想解决物理问题中“数”“理”两张皮的问题,必须坚持3个原则:数学量必须有物理量与之对应,数学操作必须符合物理规律,数学结论必须具备物理意义．涉及到运用导数和积分解决运动图像问题,就必须首先分析和解决好,数学的“斜率”或“面积”的物理意义问题．

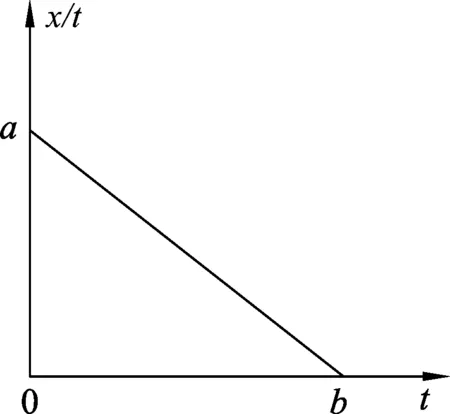
图6

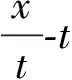
(B) 物体的初速度大小为b.

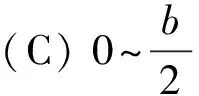
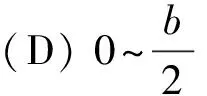
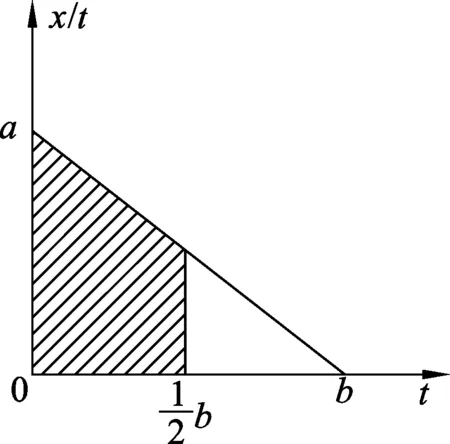
图7

解析： 有学生认为,速度-时间图像中,位移对应图像中速度图线与时间轴所围成的“面积”,本题中,纵坐标是位移与时间的比值,即平均速度,横坐标是时间,也属于“速度-时间”图像,位移就应该对应平均速度图线与时间轴所围成的“面积”,如图7中阴影部分面积．很明显,学生的分析过程出现了“面积”与“位移”的错误对应．

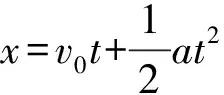
(1)

同时,关系式对时间t求导后得到

x′(t)=v(t)=v0+at.

(2)

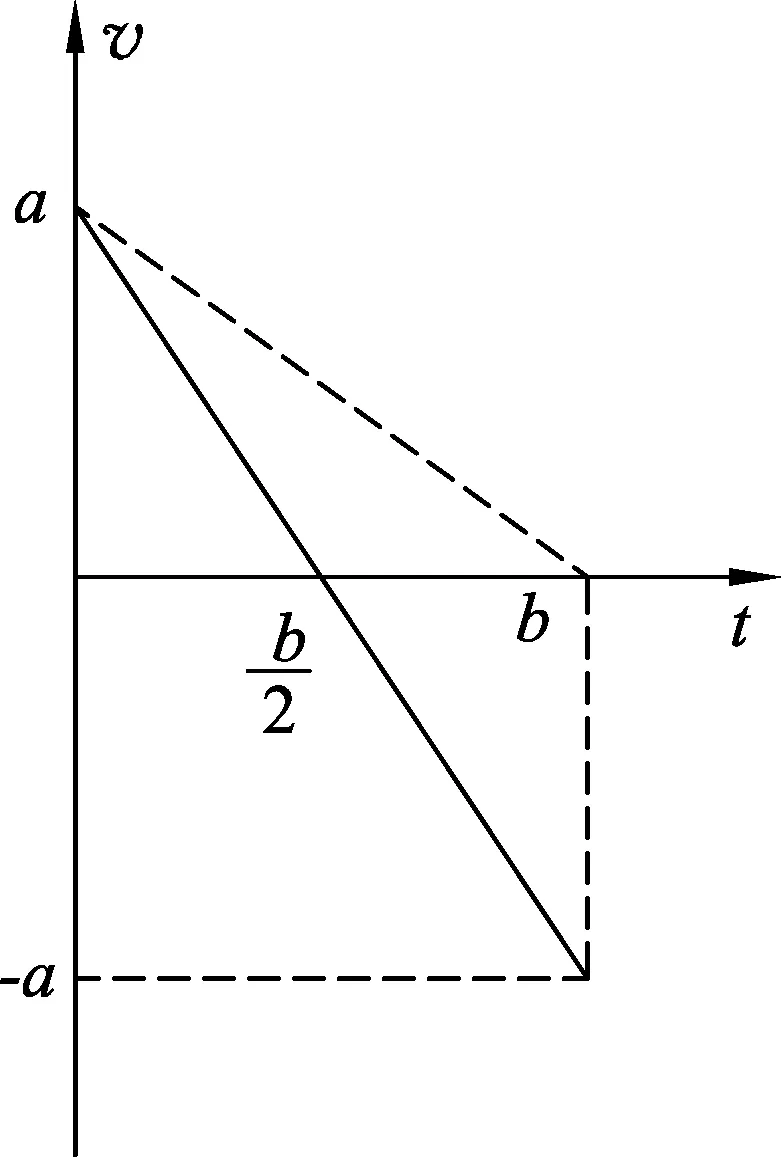
图8

比较(1)、(2)两式的可获得两个有用信息: ① (2)式中所对应的函数图线斜率是(1)式对应函数图线斜率的2倍．② (1)式的图像中纵轴截距与(2)式图像中纵轴截距物理意义相同——均表示物体运动的初速度,即v0=a．据此,可以作出v(t)=v0+a′t的图像,如图8中实线(虚线为平均速度与时间图线)．

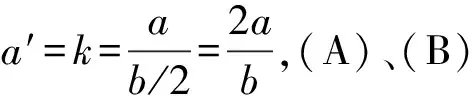
由以上例题分析可见,导数和积分的数学方法为解决图像问题提供有力支持,可以揭示运动图像丰富的物理内涵．在高中物理教学中,教师应当注重培养学生“数理结合”的能力和理解图像、分析图像和应用图像的能力,要求学生能用合理的数学方法分析物理问题,能用数学结果解释物理现象,物理量与数学量对应关系的准确把握则是解决问题的关键,真正将“数理结合”思想融合在物理学习过程中．