解题与命题视角的差异对物理习题教学的启示

潘岳松

(江苏省海门中学,江苏 海门 226100)

学生在解答物理习题的过程中,会出现各种各样的解法,对学生各种不同的解法进行统计和分析,可以看出学生解题时采用的视角和思维的具体路径;与此同时,对物理习题的命制进行分析,从而揣摩、把握命题者的考查意图.通过比较学生解题视角和命题者命题视角存在的差异与分歧,并分析造成这种差异的原因,寻找优化中学物理习题教学的方法与举措.

1 解题与命题视角的差异

以两道物理习题的具体解答为例,在概括学生解题过程中所采用的典型视角、思路方法后,进一步揣摩命题者命题的意图,可以直观看出两者的差异.

1.1 轻质弹簧问题

图1

例1.(2013年江苏物理高考第9题)如图1所示,水平桌面上的轻质弹簧一端固定,另一端与小物块相连.弹簧处于自然长度时物块位于O点(图中未标出).物块的质量为m,AB=a,物块与桌面间的动摩擦因数为μ.现用水平向右的力将物块从O点拉至A点,拉力做的功为W.撤去拉力后物块由静止向左运动,经O点到达B点时速度为0.重力加速度为g.则上述过程中

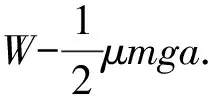
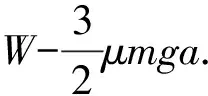
(C) 经O点时,物块的动能小于W-μmga.

(D) 物块动能最大时弹簧的弹性势能小于物块在B点时弹簧的弹性势能.

1.1.1 解题的视角

视角1:功能关系(学生用得最多).

如图2所示,设物块到达A、B点时弹簧弹性势能分别为EpA、EpB,物块到达O点时动能为Eko,由功能关系，第1次从O→A,

图2

EpA=W-μmgxOA.

(1)

第1次从A→O,

EpA=EkO+μmgxOA.

(2)

第1次从O→B,

EkO=EpB+μmgxOB.

(3)

由EpA>EpB,xOA>xOB,AB=a,得

(4)

(5)

设B关于O对称的点为B′,则物块在到达B或B′点时,弹簧的弹性势能均相等．物块动能最大时,物块受到地面的滑动摩擦力等于弹簧的弹力,可以分3种情况讨论.

(1) 物块在B′点时动能最大,有kxOB′=μmg,根据功能关系,EkO=2μmgxOB.

(2) 物块在B′左侧C点时动能最大,同理有kxOC=μmg,EkC=μmg(xOB+xOC).

(3) 物块在B′右侧C′点时动能最大,同理有kxOC′=μmg,EkC′=μmg(xOB+xOC′).

由于动摩擦因数μ和弹簧劲度系数k均为未知,上述3种情况均有可能,(D)选项错误.

视角2:极限法(少部分学生采用).

假设摩擦力足够大,则物块速度变为0的B点更加靠近O点,而物块动能最大时的位置更加靠近A点,摩擦力不同,物块最大动能时的位置也不确定,(D)选项不能给出判断.

视角3:赋值法(少部分学生采用).

采用赋特殊值法进行定量计算,可以对前3个选项进行判断,但是对(D)选项容易出现误判,因为动摩擦因数、弹簧劲度系数不同的取值会影响结论的得出.

1.1.2 命题者的视角

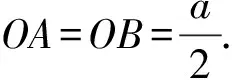
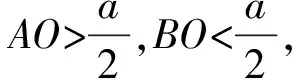
图3

由以上分析,本题模型实质是弹簧拉着物块做振幅不断减小的简谐运动.对本题可以根据对称的思想和简谐运动模型来分析,也可以用功能关系来分析.

点评:从学生解题视角来看,本题物块的受力与运动过程容易分析清楚,但由于题中涉及弹簧变力做功、摩擦力做功、动能及弹性势能的变化等多种影响因素,解答起来难度很大,尤其是(D)选项,只有极少数学生能够给出正确的解答.部分学生由于解题时间限制和思路受限,更倾向于采用定性分析和特殊方法来解答本题.

从命题者命题视角看,不论学生是否学过简谐运动的知识,只要认识到解决本题的两个突破口,即何处摩擦力等于弹簧弹力(平衡位置)、制约物体动能最大值的因素(动摩擦因数、劲度系数),进而将定性分析和定量计算结合起来,他们就会很快做出正确的判断.

1.2 平抛运动问题

例2.如图4所示,在水平面上有一个半圆形的坑,在坑的左边沿有一个物块以一定初速度v0沿水平方向飞出,物块落到坑上时其速度方向与初速度方向夹角为θ,当v0从很小值(趋近于0)逐渐增大时,对应的θ角变化情况是

(A) 一直变大. (B) 一直变小.

(C) 先变大后变小. (D) 先变小后变大.

1.2.1 解题的视角

视角1:速度偏角(学生最容易想到的).

图5

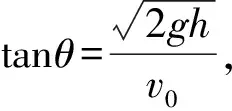
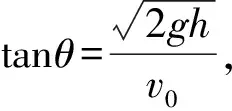
视角2:平抛运动推论.

视角3:赋值法.

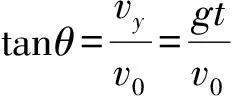
视角4:极限法.

若初速度无限趋近于0,则物块在水平方向上前进极小距离,竖直方向做自由落体运动,故物块落点速度偏角很大;若初速度趋近于无限大,则物块在竖直方向上几乎没有下降,而水平方向前进了极大距离,故物块落点速度偏角很小.

极限法可以很好地比较落点在圆弧左右两端点附近速度偏角大小情况,可是对于落点在圆弧中间位置附近的情况,要有合适的初速度(不能极大或极小),假设各落点高度自左向右先增大后减小,速度偏角的变化趋势是否能一直增大或一直减小无法判断.

视角5:定量计算(极少数学生采用的做法).

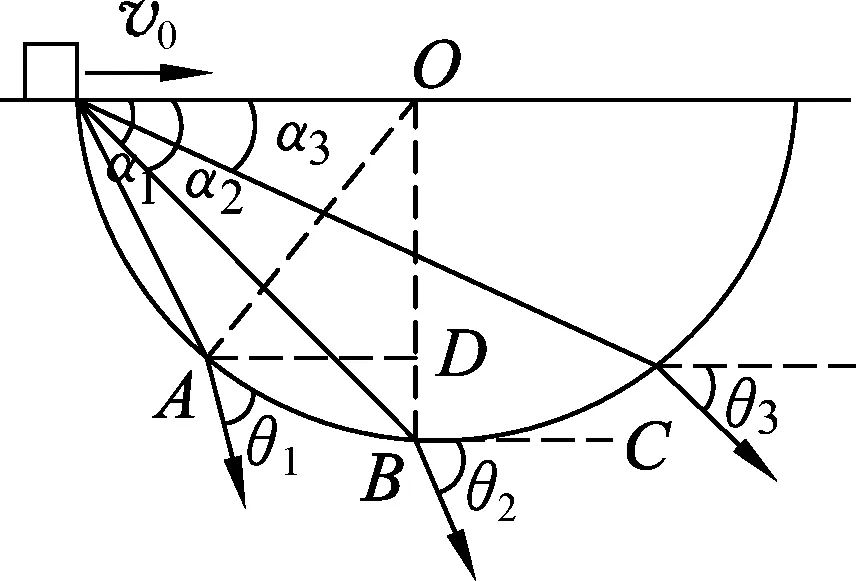
图6

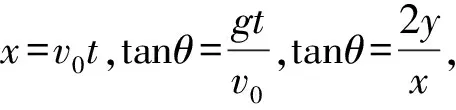
1.2.2 命题的视角

如图6所示,随着落到坑上的点在水平方向右移,物块做平抛运动的位移方向越来越接近水平方向,因此位移偏角α越来越小,根据平抛运动速度偏角与位移偏角的关系,做平抛运动的物体任一时刻瞬时速度偏角的正切值是从初始时刻到该时刻位移偏角正切值的2倍,即tanθ=2tanα,可知,速度偏角越来越小,故(B)选项正确.

点评:学生在解题过程中用了5种方法,基本都是根据题目的已知信息来顺向解题,前4种方法都不能得到最后结果,定量法虽然能得到最后结果,但计算繁杂,也容易出错.而命题者希望学生能根据平抛运动速度偏角与位移偏角关系来反向解题,直接得出结果.

学生在思维受阻时,若能换个视角考虑问题,即随着物块落点的右移,有没有变化趋势始终一致的变量,进而从这个变量(位移偏角)入手,就会顺利解决本题.

2 解题与命题视角差异的产生原因分析

无论是新授课的学习,还是复习课的学习,对学生来说,都是一种新知的学习.他们在解题时,并没有明确的解题计划,体现的是一种“新手”思维,遵循“算法驱动”思路,即从局部开始,“自下而上”,步步为营,通过逐步推导的方式来解题.

而命题者秉持的是一种“专家”思维,遵循“目标驱动”思路.命题时先确定习题要考查的目标,如学生对某个物理观念的认识情况,运用物理模型解决实际问题的能力等,再加工来自教材、文献或者生产生活实际的物理素材,将物理原理、模型中涉及到的物理量设置为已知量和未知量两类,进而创设问题情境、设置问题呈现条件,将显性的线索改为隐含的线索,并提出合适的问题.命题者期待学生能发现已知、未知条件之间的各种内在关联,采用“自上而下”的解题策略,“一眼”看出问题的关键.

命题者不断给题目“加套”,力图考查出学生在物理观念、原理、模型、能力、科学本质认识等知识、能力、认识方面的水平层次,而学生解题时要不断给题目“解套”,往往囿于时间限制,多就题论题,能走到哪一步是哪一步,一旦问题表征复杂,学生思维就容易“卡壳”.

3 解题与命题视角差异对习题教学的几点启示

为缩小、弥合解题与命题视角的差异与分歧,物理习题教学要引导学生采用多元视角审题,学会构建模型,洞察问题本质,多进行说题、编题的实践.

3.1 将命题语言融入到教学语言中

在物理习题教学中,日常教学语言多表现为“这道题怎么解”、“有几种解法”、“哪些条件已知,哪些条件未知”等,而命题语言更多体现为“这道题考查哪些知识点”、“需要构建怎样的物理模型”、“考查某个物理观念的认识”等.针对命题语言在教学语言中的缺失,一方面,习题教学要引导学生学会从命题视角去审视物理习题,对物理习题逐步建立起“从什么角度考察”、“考察了什么物理原理”、“通常对该类型题目有哪些处理方法”等思考方法的习惯,以便在更高层面高屋建瓴地把握习题.

另一方面,要多采用变式教学．由于变式教学是通过对习题的各种拓展,促进学生跳出就题论题的框框,从不同角度审视习题,进行多元思考、深度思考,从而把握问题的本质,因此,变式教学的语言也可以视为一种命题语言.例如,在“匀强磁场中的动态圆问题”一节的教学中,面对表征复杂的各类动态圆问题,可以先追溯带电粒子在磁场中最原始的情景,即磁场弥漫于整个空间,粒子源发射的带电粒子以“速率不变,方向任意”、“方向不变，速率任意”两种情况运动,让学生画出粒子运动示意图,接着将问题变形,磁场分别被局限在矩形区域、三角形区域、圆形区域、环形区域中,再让学生画出各种情形下粒子运动的示意图.这种变式教学能够反映命题者命题的思考路径,即基于某个最初的问题情境,进而编制出千变万化的各类动态圆问题,在还原命题者思考路径的过程中,可以有效促进学生思维品质的提升.

3.2 重视物理模型的构建

物理模型思维是科学思维的重要方面,在培养学生物理核心素养的背景下,物理模型构建能力自然是命题者命题要考查的重点.在各类物理习题中,命题者善于将物理模型隐匿于物理现象中,需要学生能识别、构建、完善模型,为此,教学中一是要引导学生熟悉各类常见的物理模型,如斜面模型、传送带模型、子弹打木块模型、轻杆模型等,让他们脑海中的知识组块化、结构化,便于在新的问题情境中调取熟悉的模块;二是启发学生善于从生活生产实际情境中构建出物理模型,如从公园摩天轮构建出单轨道圆周运动模型,从起重机吊运货物构建出“机车启动”模型等,进而提升物理抽象建模能力;三是多给学生做建模方法的点拨,如抓住事物主要因素、忽略次要因素的方法,通过画示意图、图像来直观显示的方法,突出事物本质特征的方法等.

3.3 注重直觉思维的培养

直觉思维是对问题未经严密分析,而从整体上直接把握的一种思维形式,好的直觉思维有助于透过现象领悟、洞察事物的本质.学生遇到表征复杂的物理习题,在还没搞清楚问题细节及命题意图的情况下,直觉思维参与解题显得尤为重要.

学生直觉思维的培养,一是需要不断完善知识结构,掌握好物理学的基本概念、原理及方法,便于在新的物理情境中能够提取脑海中已有的知识贮备.如遇到电磁感应的各类物理习题,学生有了对法拉第电磁感应定律的深刻理解,就很容易提取出“杆、框切割模型”、“磁变模型”等知识组块,并迅速将其和习题中的信息进行联结.二是需要锤炼类比、联想、猜测等思维方法,促进学生思维发散,在脑海中建立丰富的物理图景.如遇到带电粒子在复合场中做圆周运动速度极值问题,可以根据等效的思想,想象等效场中的“最高点”、“最低点”.三是需要形成对物理的美感,学会欣赏,只有对物理有着美好的学科情感,才会更容易“诱发”出直觉思维.例如引导学生发现竖直上抛运动、圆周运动、等量同种电荷产生的电场、电与磁现象、光的反射等物理现象都存在对称的美,在遇到相关物理习题时,学生脑海中用对称思想处理问题的火花可能就会迸发出来.

3.4 引导学生说题、编题

物理习题命制的素材,往往都来自于教材、生产生活实际,如对教材中常规习题进行改变,包括变情境、变条件、变设问角度等,但是学生在解题过程中,一般都无暇考虑命题者是如何命题的.这无形中就失去了一个通过分析习题来提升思维品质的机会,对此,教学中可以引导学生去说题、编题.

说题对学生提出了较高的要求,一方面学生在把内隐的思想显性化的过程中,不仅明确了物理概念、规律及物理量之间的关系,还厘清了他们自身对问题尚存在的模糊的认识;另一方面学生说题不仅仅局限于说解题思路、方法要领,还要说命题意图、隐含条件等.这样就相当于将命题视角和解题视角融合,可以获得对习题全面、深入的认识.

学生编题过程类似于将他们自身和命题者进行角色互换,当学生逐渐学会了创设物理情境,设置已知、未知参数,从不同角度、不同层次设问,甚至结合他们自身的独特经历,编制出一些有创意的好题.他们在今后解题过程中,往往就能感同身受,洞悉命题者命题的意图,从而更容易解决问题.