多摩擦点平衡系统何处先达最大静摩擦状态的判定3法
2019-02-10李卫平李兴春罗强生
李卫平 李兴春 刘 丽 罗强生
(西华师范大学物理与空间科学学院,四川 南充 637009)
在力学系统平衡的题目中,涉及到静摩擦力的力学系统平衡的题目一般是较难的,而当力学系统中的摩擦点不止一个时,题目便会显得更难. 这类题目之所以难,不仅是因为存在多个摩擦点,使大小、方向均可随条件变化的静摩擦力个数增多,而更主要的是,题目往往将系统直接或间接置于平衡状态即将打破的临界状态——多摩擦点中的某些或全部处于静摩擦力达到最大的状态. 正因为如此,有关多摩擦点系统平衡的题目便频频在历年的全国高中物理奥赛中出现.
解决上述涉及多摩擦点系统平衡的题目,通常采用的方法是:不事先判断何处先达最大静摩擦状态,而是根据一般刚体的合外力为0、合外力矩为0的平衡条件列出系统的各个部分及整体的一般平衡方程,并列出各个摩擦点不出现相对滑动时静摩擦力满足的特殊平衡方程——fi≤μiNi. 再通过联立求解这些平衡方程,并辅之以根据题目特殊结构的一些分析、判断和计算,从而最终求得题目要求的结果. 这种方法的好处在于其普适性,这也正是其被通常采用的原因. 但这种方法也存在一些不足: (1) 各摩擦点静摩擦力的变化的物理过程不明晰,甚至题目虽然解出来了,但却不知道各个摩擦点究竟哪些达到最大静摩擦状态哪些未达到最大静摩擦状态. 从教学的角度看,这不利于培养学生的物理才能.(2) 由于各摩擦点均需列出静摩擦力满足的式子,所以式子数量较多,且这些式子均是不等式形式的,对其进行分析、判断一般往往较为繁琐.
其实,在这类涉及多摩擦点系统平衡的题目中,很多时候各摩擦点何处先达到最大静摩擦是可以事先判断的,先行判断之后,再完成题目所要求的解答就变得较为明确和容易了.本文所要探讨和概括的就是在3种特定情况下多摩擦点系统何处先达最大静摩擦状态的判定方法.
1 各摩擦点静摩擦因数相同、摩擦力始终相等时的判断
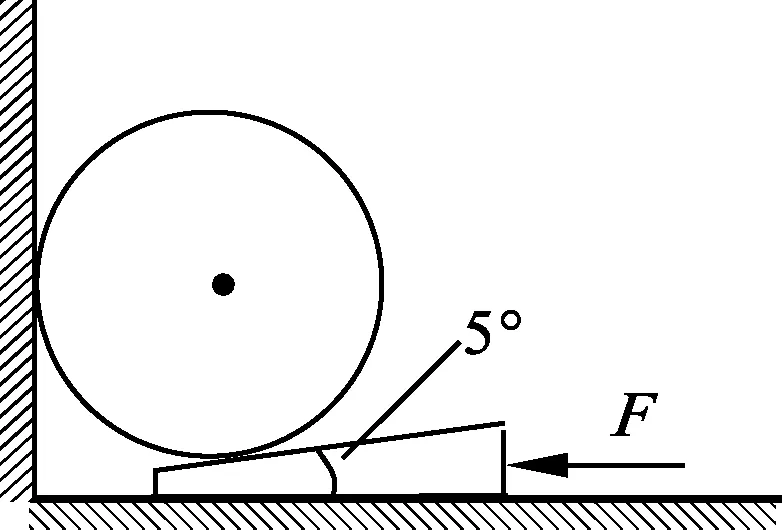
图1
当各摩擦点静摩擦因数相同时,压力较大处的最大静摩擦力便也较大.如果系统的结构又决定了各摩擦点处的静摩擦力始终相等的话,那么当压力较小的摩擦点处的静摩擦力已达最大时,压力较大的摩擦点处的静摩擦力显然尚未达到最大.于是,当各摩擦点处静摩擦因数相同、摩擦力始终相等时便可根据各处的压力大小进行判断:压力较小处必先达到最大静摩擦状态.当然,如果压力较小处的静摩擦因数也较小的话,那么更可以断定压力较小处将先达到最大静摩擦状态.
例1.如图1所示,质量为m=10 kg的匀质圆柱体放在倾角为5°的楔和竖直墙壁之间,所有接触处的静摩擦因数均是μ,μ=0.25.不计楔的重量,求水平推力F为多大时才能推动楔?
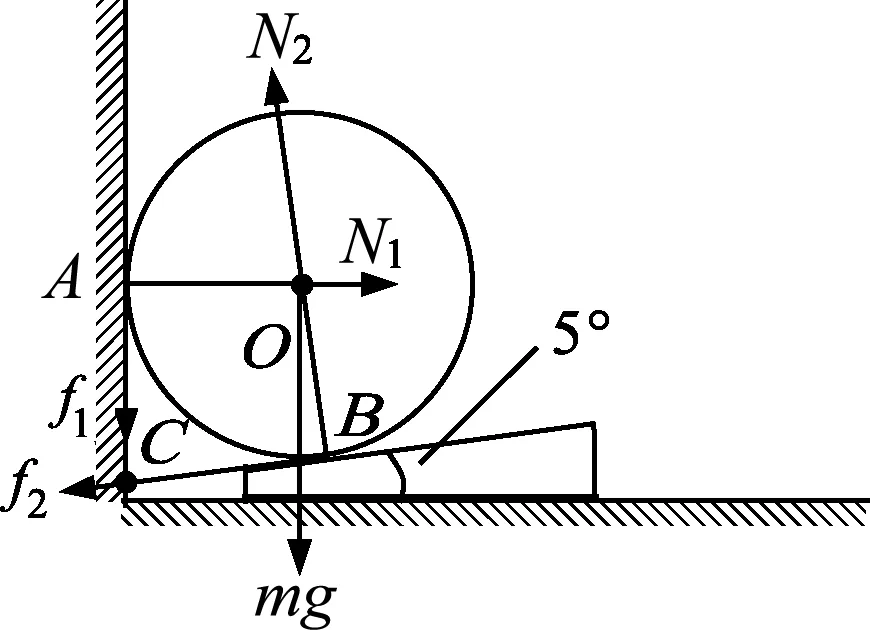
图2
解析:圆柱体的受力如图2所示,图2中,f1、N1及f2、N2分别为墙壁及楔对原柱体的摩擦力和压力. 先确定圆柱体和墙壁的接触处A与圆柱体和地面的接触处B何处先达最大静摩擦状态.
对圆柱体,由∑MO=f2r-f1r=0,即知
f1=f2.
(1)

(2)
由(2)式可知
N2>N1.
(3)
由(1)、(3)两式以及A、B两处的静摩擦因数相等的条件,便可得知A处先于B处达到最大静摩擦状态. 在A处达到最大静摩擦状态时
f1=μN1.
(4)
对圆柱体,由
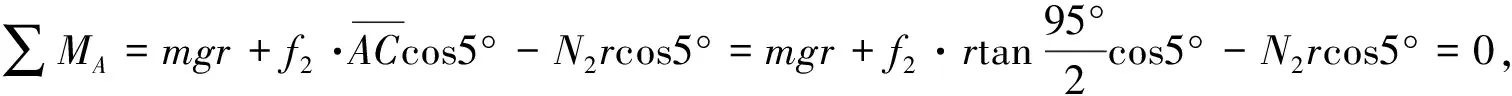
(5)
由(1)、(2)、(4)、(5) 4式解得
N2=103.8 N,f2=3.0 N.
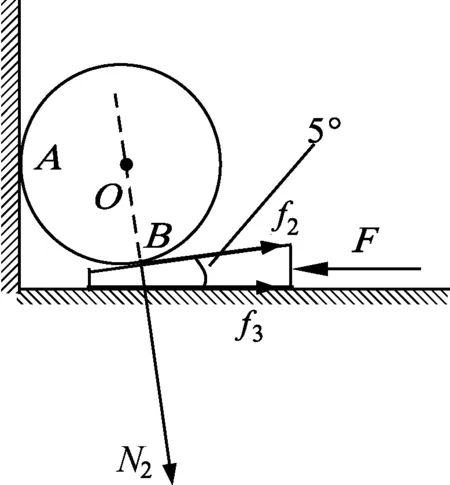
图3
楔受力如图3所示. 要推动楔子,所需的水平推力至少为
Fmin=f3+f2cos5°+N2sin5°=μN2cos5°+f2cos5°+N2sin5°.
将已得到的N2、f2之值代入,最终可计算出
Fmin=37.8 N.
2 各摩擦点静摩擦因数相同、压力始终相等时的判断
当各摩擦点处的静摩擦因数相同、压力也始终相等时,各摩擦点处所可能达到的最大静摩擦力也必定相等.如果系统的力学结构又决定了各摩擦点处的静摩擦力大小始终不相等的话,那么,静摩擦力较大处的静摩擦力已达最大时,静摩擦力较小处的静摩擦力显然尚未达到最大.所以,当各摩擦点处的静摩擦因数相同、压力始终相等时便可根据各处静摩擦力的大小进行判断:静摩擦力较大处必先达到最大静摩擦状态.当然,如果静摩擦力较大处的静摩擦因数较小的话,那么更可以断定静摩擦力较大处将先达最大静摩擦状态.
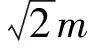
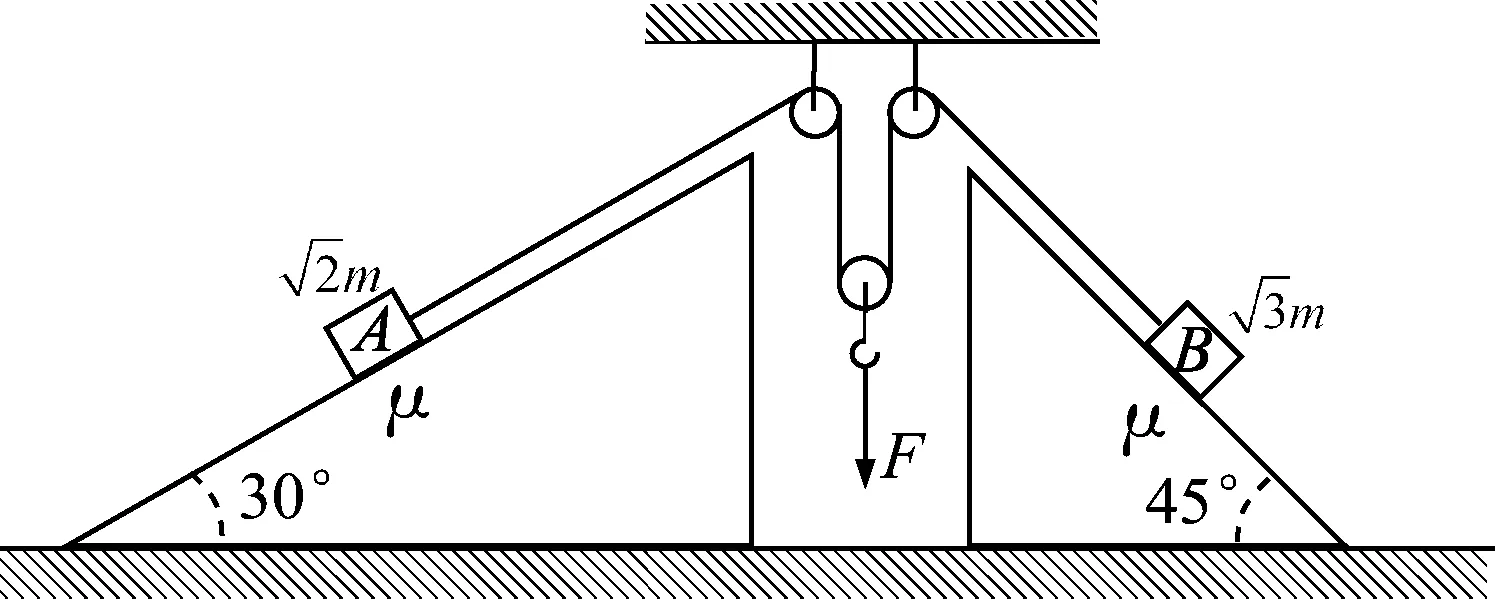
图4
解析:根据静摩擦因数和斜面倾角的大小容易判断,即使不加拉力A、B两物体也不会沿斜面下滑, 所以拉力F的下限Fmin=0. 下面求其上限Fmax.
A物体与斜面间的压力为
B物体与斜面间的压力为
A物体与斜面间的静摩擦力为
B物体与斜面间的静摩擦力为
由于NA=NB,μA=μB=μ,fA>fB, 所以A物体较B物体先达到最大静摩擦状态. 当A物体达到最大静摩擦状态时,所加的拉力达到允许的最大值. 此时
3 各摩擦点压力、静摩擦力始终相等时的判断
当各摩擦点的压力始终相等时,静摩擦因数较大处可达到的最大静摩擦力也较大.如果系统的力学结构又决定了各处的静摩擦力始终相等的话,那么,当静摩擦因数较小处已达最大静摩擦状态时,静摩擦因数较大处显然尚未达最大静摩擦状态.所以,当各摩擦点处的压力、静摩擦力始终相等时,便可根据各摩擦点处的静摩擦因素大小进行判断:静摩擦因数较小处必先达到最大静摩擦状态.当然,如果静摩擦因数较小处的压力也较小的话,那么更可以断定静摩擦因数较小处将先达到最大静摩擦状态.
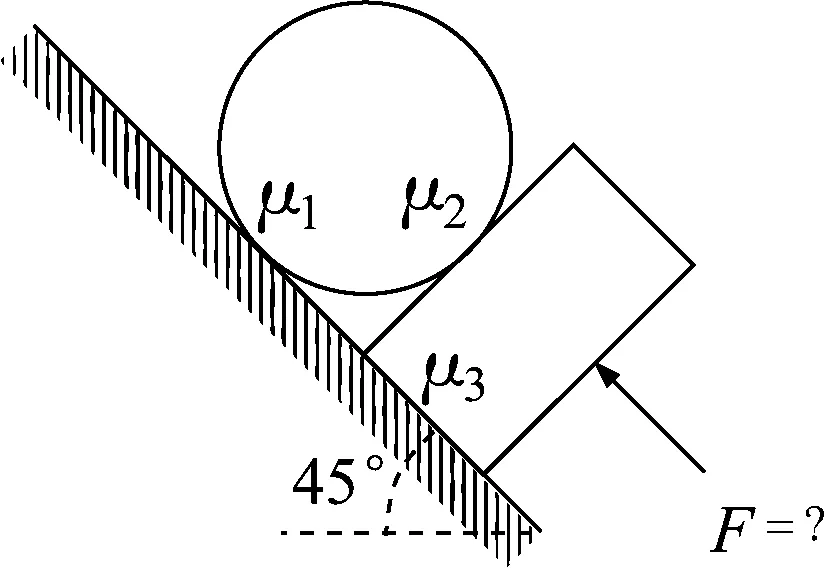
图5
例3.如图5所示,质量为m的圆柱体搁置在倾角为45°的斜面与挡板所夹的直角中.圆柱体与斜面、挡板的摩擦因数分别为μ1=0.8、μ2=0.5. 挡板与斜面的摩擦因数为μ3=1.0,挡板的质量为2m. 现用垂直于挡板的力F推着挡板使圆柱体从静止开始沿斜面缓慢向上运动, 求所需的F为多大.
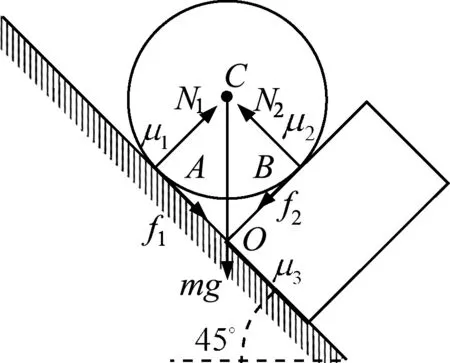
图6
解析:圆柱体沿斜面缓慢向上运动时,其受力如图6所示,N1、f1及N2、f2分别为圆柱与斜面及圆柱与挡板的压力和摩擦力. 可能圆柱与斜面的接触处A处于滑动静摩擦状态而圆柱和挡板的接触处B处于静摩擦状态,圆柱作平动;也可能B处处于滑动摩擦状态而A处处于静摩擦状态,圆柱沿斜面作纯滚动. 究竟是那种情况这需要先进行判断.
由∑MO=N1R-N2R=0,可得知N1=N2.
由∑MC=f1R-f2R=0,可得知f1=f2.
又因为μ2<μ1,所以在圆柱体从静止开始运动的过程中,必定是B先达到最大静摩擦而后B处便开始滑动,圆柱体从而沿斜面向上作纯滚动.
下面计算力F的大小为
对圆柱体,由∑MA=0得到
(1)
又有
f2=μ2N2.
(2)
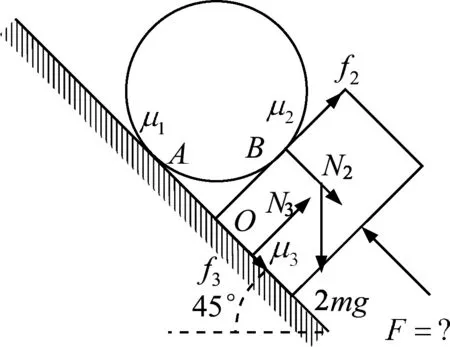
图7
对挡板,其受力如图7所示.由沿斜面方向和垂直斜面方向上其所受合外力为0得
(3)
(4)
由(1)~(3)式解得
(N3>0表明挡板与斜面间确实存在压力作用,不至于因为f2过大导致挡板与斜面间的压力消失)
将这些结果代入(4)式即得
4 结束语
上述3种方法指出了在3种特殊情况下如何判断多摩擦点平衡系统何处达到最大静摩擦.但在解答有关多摩擦点系统平衡题目时,不可机械套用这些方法.需注意以下3点.
(1) 在某些多摩擦点系统平衡题目中,系统的结构明显决定了各摩擦点处的物体接触部位将同步开始相对滑动,此时各摩擦点必定同时达到最大静摩擦状态.在这样的情况下,就不必再用上述3种方法进行判断.
(2) 在某些多摩擦点系统平衡题目中,系统的结构和摩擦点处的静摩擦因数决定了系统某些处或者处处会处于自锁状态.这些处于自锁状态的摩擦点处必定不可能达到最大静摩擦状态.在这样的情况下,也同样不必再用上述3种方法进行判断.
(3) 多摩擦点系统平衡的题目并不限于上述3种特殊情况,上述3种方法是不可能对任何多摩擦点系统何处达最大静摩擦状态均能作出判断的.在其他情况下,应如何对多摩擦点系统何处达到最大静摩擦状态作出判断,是一个尚需探讨的问题.
