基于SOA⁃Newton迭代的六自由度平台正解算法

陈泽栋，卢明涛，闵跃军，马建明，丁祝顺，王宏建

（北京航天控制仪器研究所，北京100039）

0 引言

六自由度并联平台采用Stewart结构，相较于传统的串联平台，其具有刚度大、精度高、运动空间广、承载能力强、响应速度快、误差不累积等优点，被广泛地应用于运动模拟、机械加工和精密定位等领域［1⁃2］。六自由度平台位姿正解是设计和研究运动学、动力学和轨迹规划的前提，也是后续实现高精度位姿控制的基础。与串联机构相比，由于并联机构各个电动缸之间存在着强耦合关系，运动学正解需要求解一组含有六个未知数的非线性方程组，因此其运动学正解相对困难［3］。

国内外学者采用了大量方法对Stewart平台运动学正解进行了研究。天津工业大学钟有博［4］在Simulink软件中利用Newton迭代的方法实现了运动学正解，但是由于每次迭代时都需要对方程组的Jacobian矩阵进行求导，导致了算法的求解时间较长，难以用于实时系统。为了改进这一问题，耿明超等［5］采用拟Newton法来进行求解，利用当前函数值代替Jacobian矩阵，从而避免了矩阵运算，降低了计算量。但是无论采用何种方式进行迭代，都需要人为的提供一个迭代初值给算法，迭代初值会一定程度的影响求解的精度和速度。为了解决这一问题，陈莉等［6］、弓瑞等［7］采用智能计算的思想，将粒子群算法和遗传算法应用在六自由度并联机器人的正解问题上，利用粒子群算法的全局搜索能力来进行正解，在6⁃SGP机构上验证了该算法的可行性。但是，粒子群算法和遗传算法在后期会出现收敛速度慢的现象，偶尔还会收敛到局部最优点，难以应用在工程实际中。

为了解决智能算法后期搜索效率降低和Newton法对初始点敏感的缺陷，本文提出一种基于人群搜索算法（Seeker Optimization Algorithm，SOA）的Newton迭代混合算法用于六自由度平台运动学正解，算法的实现原理如图1所示。已知六个电动缸长度后，利用人群搜索算法进行运动学正解，将得到的位姿作为Newton迭代的初始值，然后利用Newton迭代算法进行进一步的求解，从而得到更加精确的位姿。最后，利用运动学反解求得该位姿对应下的电动缸长度，与已知的电动缸长度进行对比验证。

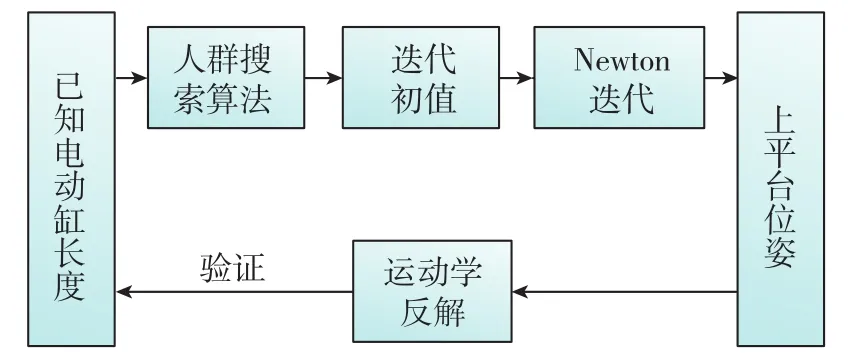
图1 SOA-Newton算法正解原理图Fig.1 Schematic diagram of SOA-Newton hybrid algorithm

1 运动学正解数学模型

六自由度位姿平台基于Stewart机构，如图2所示，主要由上平台、下平台以及连接上下平台的6个电动缸构成。电动缸与上下平台之间通过虎克铰连接，运动平台工作时，上位机通过控制六个电动缸的长度来改变上平台姿态，进而实现空间六个自由度的运动。为了便于建模，对位姿平台进行结构简化，在上平台建立动坐标系Ob⁃XbYbZb，在下平台建立静坐标系 Oa⁃XaYaZa。设电动缸与上平台的铰点坐标为 Bi（i＝1，2，…，6），与下平台的铰点坐标为 Ai（i＝1，2，…，6），铰点为120°对称分布，上平台外接圆半径为Ra，铰点最短距离为ha，下平台外接圆半径为Rb，铰点最短距离为hb。

图2 六自由度运动平台结构简图Fig.2 Schematic diagram of 6-DOF motion platform

上平台在运动过程中可以用六个变量来表示α、β、γ、x、y、z的姿态。其中，α、β、γ为绕 X轴、Y轴、Z轴分别旋转的横滚角、俯仰角、偏航角，旋转的方向遵循右手定则；x、y、z表示沿 X轴、Y轴、Z轴的平移量，根据空间坐标旋转规则可以确定动坐标系到静坐标系变换的旋转矩阵R为

确定旋转矩阵和平移矩阵后，上铰点Bi坐标由动坐标系变换到静坐标系的坐标变换公式为

六自由度位姿平台正解问题是已知电动缸上下铰点之间的长度去求解上平台位姿。设未知变量 x＝［x1x2x3x4x5x6］T＝［α β γ x y z］T，已知变量为给定杆长L＝［L1L2L3L4L5L6］T，实际杆长与初始杆长的杆长差计算公式为

根据物理意义可知，函数fi（x）的最小值为零，因此可构建运动学正解的优化模型

模型的约束条件为上平台允许的最大运动空间。

2 SOA⁃Newton算法的基本思想

SOA⁃Newton混合算法的基本流程为：首先进行种群初始化，设置种群规模、最大迭代次数、边界条件等；接着计算个体适应度，寻找个体最优和全局最优；确定搜索的方向和步长，进行种群位置更新，当进化到一定代数后，将SOA算法的结果作为初始迭代位姿进行Newton迭代；设置Newton迭代求解精度和最大迭代次数进行Newton迭代，满足输出条件后迭代的值即为平台的位姿正解。混合算法利用SOA算法的全局搜索能力对Newton迭代初值进行补偿，其算法的基本思想及实现流程如图3所示。

图3 SOA-Newton混合迭代算法流程图Fig.3 Flow chart of SOA-Newton algorithm

2.1 SOA算法基本原理

SOA算法模拟人的随机搜索行为，即在连续的搜索过程中，当搜寻者所处位置较优时，应该在较小邻域内进行搜索；当搜寻者位置较差时，应该在较大的邻域内搜索。SOA算法将这种策略应用于解决优化模型最优解的问题，其搜索方向和步长更新规则如下［8］：

（1）步长更新

SOA搜索算法的步长更新规则为：如果适应度函数值小，表明结果靠近最优点，则搜索步长也小；如果适应度函数值较大，则表明位置不理想，应采用较大步长跳出当前位置［9］。搜索步长变量采用Guass函数来描述

式（5）中，uA为Guass隶属度，x为输入变量，u、σ为隶属度函数参数。当输入变量超出3σ时可以忽略，故设定最小隶属度为0.0111，最大隶属度为1。为了使目标函数值的排列顺序成正比，采用线性隶属函数

式（6）中，ui为目标函数值i的隶属度，Ii为种群降序排列后的序列编号。

根据不确定推理隶属度函数，可以确定步长为

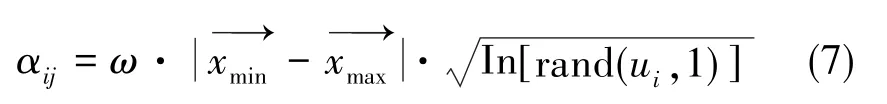
式（7）中，αij为j维空间中的搜索步长，ω为惯性权值。为了提高SOA算法的全局搜索能力，采用非线性动态惯性权重。

（2）方向更新

搜索方向需要综合利己行为、利他行为和预动行为来确定，更新规则如下

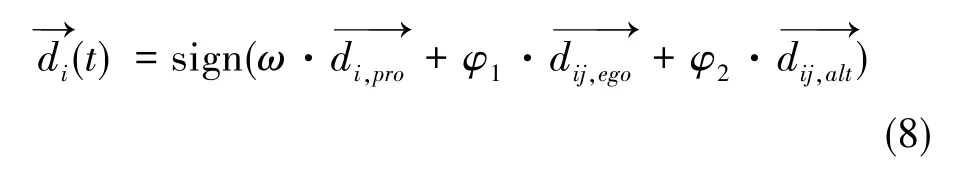
（3）位置更新

当搜索步长和方向确定后，位置可根据式（10）确定

2.2 Newton-Raphson迭代算法原理

Newton⁃Raphson迭代法是一种用来求解复杂多元非线性方程组f（x）＝0的简单数值解法，只要初值选的合理，经过一定的迭代，总会达到收敛精度［10］。下面给出 Newton⁃Raphson 迭代在六自由度正解中应用的方法，设定方程的初始解为x0，在x0处对方程组f（x）作一阶Taylor展开

式（11）中，σ（x）为高阶无穷小量，在此可以忽略，可得

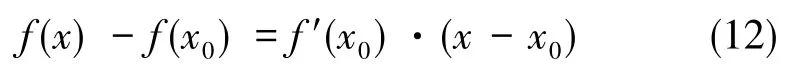
代入六自由度平台的杆长计算公式并展开可得六自由度运动平台的正解迭代模型，如式（13）所示。可以看出，上平台位置和姿态的变化量与杆长的伸缩量存在着对应关系。

对于六自由度并联平台来说，其初值x0＝［x1x2x3x4x5x6］T＝［α β γ x y z］T为上平台的姿态和位置信息，ΔL为电动缸长度的变化值，ΔX为位置和姿态的变化值。在Simulink软件中建立了利用Newton迭代法求解六自由度平台正解的仿真模型，如图4所示，inverse motion模块中电动缸长度计算模型如图5所示。模型的终止条件为：达到最大迭代次数N或最大误差max（Δx）＝xk-xk-1＜ ε，此时求解的结果即为上平台位姿。

图4 Newton-Raphson迭代法Simulink仿真模型Fig.4 Simulink model of Newton-Raphson iteration method

图5 电动缸长度计算模块Fig.5 Calculation module of electric cylinder length

3 SOA⁃Newton算法的正解实例

3.1 六自由度平台的参数设定

以实验室研制的车载位姿平台为例，如图6所示，该平台能够根据外界反馈到的车体位姿调整上平台姿态，使其保证在水平状态。对该系统进行简化，得到其上平台半径为Ra＝0.4m，下平台半径为Rb＝0.54m，上平台相邻连点间的最短距离为ha＝0.1m，下平台相邻连点间的最短距离为hb＝0.2m，平台处于工作零位时电动缸上下铰点之间距离为0.72m。系统选用滚珠丝杠型电动缸，最大行程为150mm，能够实现上平台三个线位移±0.2m、三个角位移±15°的运动。

图6 车载位姿平台Fig.6 Vehicle attitude platform

3.2 基于SOA迭代算法正解仿真

首先，使用SOA算法对六自由度平台进行位置正解，设定种群规模为150，最大进化代数为300，最大隶属度值为 0.95，最小隶属度值为0.0111，权重最大值为0.9，最小值为0.1。由于该平台的最大位移为±0.2m，因此将粒子群算法中的粒子空间约束在±15°内，留有一定的余量。接着，均匀选取上平台由初始点（0m，0m，0m，0°，0°，0°）运动到 （0.2m，0.2m，0.2m，15°，15°，15°）过程中的4组位姿，将这4组姿态进行运动学反解，得到对应的4组杆长。

利用SOA算法对这4组杆长进行运动学正解，求取上平台位置和姿态，计算结果如表1所示。可以看出，空间位置的最大误差在4mm以内，空间姿态的最大误差在0.3°以内，与位姿平台精度要求还有一定的距离。一般情况下，可以通过改进粒子群算法或者提高种群数量和迭代次数来提高求解精度，但是六自由度正解模型具有高度的耦合性、非线性，以上方法对精度的提高效果有限。以第4组杆长正解为例，SOA正解过程中适应度曲线变化如图7所示。由适应度变化曲线可以看出，在进化70代之后，函数的适应度值变化并不明显，这表明此时求得的值已经很接近真实值，继续进行迭代只会导致计算时间大幅延长，对于提高求解精度意义不大。

表1 四组杆长下对应的SOA算法正解结果Table 1 Calculation results of SOA algorithm corresponding to four rod lengths

求解过程中，姿态和位置的最大误差变化曲线如图8所示。由变化曲线可以看出，在进化的前1/3过程中，位置误差和姿态误差都曾下降到一个比较小的值，表明种群已经搜索到一个比较接近真实值的解。而且整个进化过程中三个位置方向的最大误差基本能保证在0.06m以内，最小值能够达到0.002m以下；姿态误差基本能够保证在2.5°以内，最小的误差值在0.05°左右，仍有提高的空间。

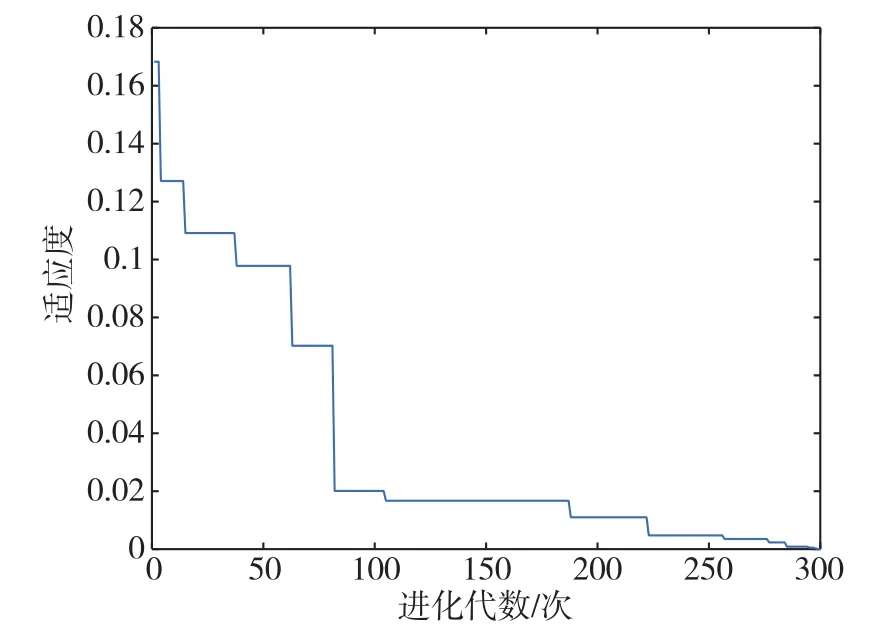
图7 求解过程中的适应度变化曲线Fig.7 Fitness curve during the solution process

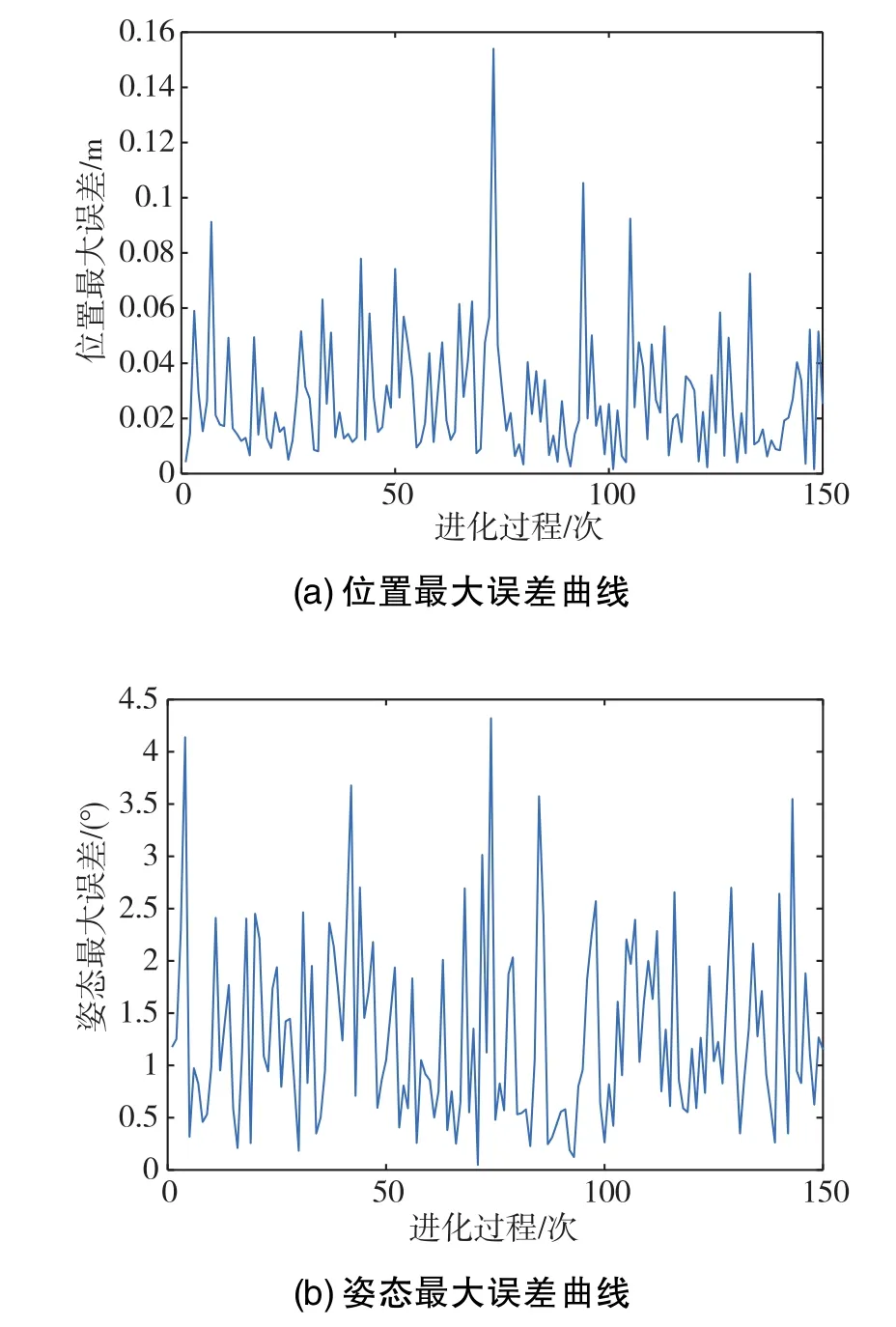
图8 迭代过程中的最大误差变化曲线Fig.8 Maximum error curves during the solution process

为了提高结果的精度，需要利用 Newton⁃Raphson算法进行进一步求解，设置 Newton⁃Raphson算法的迭代精度为1×10-6m，最大迭代次数为15次，将表1中SOA算法的计算结果作为迭代初值进行Newton迭代求解。同时，为了研究不同迭代初值对计算精度和速度的影响，对比了初值为平台工作初始位置时Newton迭代算法的计算结果，如表2所示。可以看出，在达到同等的求解精度情况下，使用SOA算法迭代的结果作为初始值进行Newton正解，能够明显减小迭代次数，从而缩短计算时间，为位姿平台后续的实时控制打下基础。

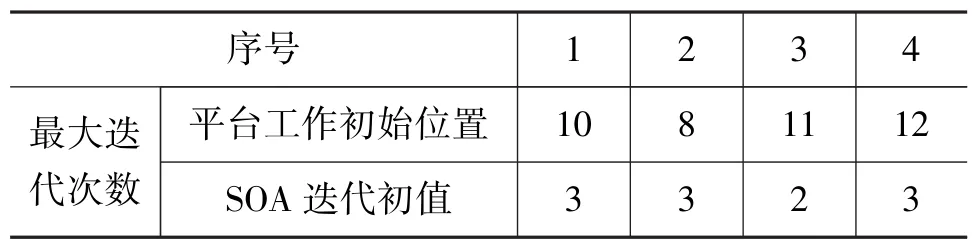
表2 不同初值下Newton算法迭代次数Table 2 Number of iterations under different initial values

3.3 SOA-Newton算法正解的实际验证

为了验证该算法在实际使用过程中的计算精度和速度，以车载位姿调节平台为对象进行混合算法正解实验。设定上平台的运动轨迹使其在工作空间内绕X轴（横滚）和Z轴（偏航）方向作一个复合的正弦运动，运动幅值为2°，频率为 0.5Hz，初始相位差为180°，运动轨迹如图9所示。为了兼顾求解的效率和精度，设置SOA算法的最大迭代次数为30次，Newton迭代算法的最大迭代次数为8次，杆长迭代精度为1×10-6m。实验结果如图10所示，可以看出由于六自由度平台六个自由度之间存在着耦合关系，算法正解的精度在上平台运动到最大位姿时会出现较大的波动，存在一定的周期性，这表明计算精度与上平台所处位姿存在一定的联系。除此之外，整个求解过程中姿态误差基本保持在0.0005°以内，位置精度基本在0.01mm以内，而且每次求解都保证在10ms以内，验证了该算法应用在六自由度并联位姿平台正解上的求解精度和求解效率，能够满足工程实际使用。

图10 正解结果与理论值的误差曲线Fig.10 Error curves of the forward solution value and the theoretical value

4 结论

本文首先对六自由度并联位姿平台的运动学进行了分析，建立了六自由度平台正解数学优化模型。针对Newton⁃Raphson算法求解精度受迭代初值影响大的问题，提出了一种基于SOA算法的Newton迭代混合算法，并在Simulink中搭建了相应的仿真模型。接着均匀选取了上平台由平台工作初始位置运动到极限位置过程中的4组姿态下对应的4组缸长，对其进行运动学正解，验证了混合算法的求解精度和速度比单纯使用Newton迭代算法和SOA算法要好。最后以实验室研制的六自由度位姿平台为例，对其进行实时正解实验，计算的结果表明，该算法在满足精度要求的同时能够兼顾求解速度，可应用于六自由度并联平台的测试开发和实时控制。