基于三频外差法的异构铸件三维测量系统

惠宏超，严小军，罗凯元，张晓玲，王 静

（1.国防科技工业超精密机械加工技术创新中心，北京100039；2.北京航天控制仪器研究所，北京100039）

0 引言

航天惯性平台及捷联惯性测量单元中的关键结构铸件均为复杂多面体结构，在加工之前必须对铸件（或粗加工零件）的各项关键尺寸和加工余量（2mm～3mm）进行测量，以保证后续精密加工的顺利完成。而现有的划线方法存在检测时间长（＞4h）、对检验者熟练程度要求高、检测精度较低等问题，使得零件的检测效率低，误检率高，成为影响型号研制进度的显著因素，由此产生了对异构铸件进行三维测量的急迫需求。与此同时，基于结构光的三维测量技术［1］的快速发展，产生了包括Fourier变换轮廓术、调制度测量轮廓术［2］、相位测量轮廓术等成熟应用的方法。随着制造行业的强力牵引，基于多频外差和数字投射技术得到了快速发展，具有更高的检测精度和效率，且抗干扰能力强，已经在智能制造、航空航天、逆向工程、医疗设备和机器视觉系统等领域得到广泛应用。

近年来，国内外许多专家学者在三维光学测量领域做了大量的研究工作，如美国Kentucky大学团队在数字投影结构光非线性分析校正［3］和高速结构光三维测量［4］方面提出了结构光三维测量技术，利用绝对相位编码技术实现了物体的高速三维测量。Zhang等［5］提出了三色相移法，对彩色图像里的RGB三色信息进行2π/3相移，测量过程只需两幅图，提高了测量速度。艾佳等［6］基于三频外差和单目视觉原理，利用投影模块的快速投影和CCD相机同步采集，搭建了一套微小视场（8mm×6mm）下物体表面形貌的测量系统，并成功重建了以硬币为代表的小视场物体在100μm深度范围内的表面三维形貌。郭进等［7］利用针对格雷码与相移结合技术在测量物体边缘位置解相位误差大的问题，采用多频外差原理研制了一套三维测量系统，系统能够完成复杂面型测量且获得高精度的点云数据，测量标准偏差为0.03mm。

本文在上述研究的基础上，根据被测铸件的异构特点以及加工对检测效率、精度的要求，设计实现了铸件的三维测量系统。该系统使用了相位光栅法［8］，利用三频外差原理［9］对投影的条纹图像进行相位展开。三频外差法所需投影的条纹较少，具有较高的测量精度和速度，尤其适用于静态物体复杂表面的形貌测量。本文的测量系统使用两组CCD相机与成像镜头组成双目视觉系统，将数字光处理（Digital Light Processing，DLP）芯片开发的投影组件投射标准正弦条纹到被测零件表面，软件同步触发控制CCD相机接收条纹图像，对图像进行三频外差算法处理之后，实现对被测零件表面形貌的三维重建与测量。

1 相机标定

相机标定是三维测量的关键一步，标定结果的好坏直接影响最终的测量精度。要确定空间坐标系中的物点与它在图像平面上像点之间的对应关系，就必须通过标定求取这种对应关系之间的未知参数。本文将标定的参数分为固定参数和可变参数，固定参数是指CCD相机像素之间的纵横比μxy，它与CCD驱动频率和图像采集卡的采集频率有关，表现为水平方向上实际像素的间距与CCD的加工尺寸不一致［10］。对固定参数的标定采用图像处理技术，由CCD相机拍摄获取标准模板圆的图像，如图1所示。对图像进行处理和圆拟合，得到拟合圆轮廓各点的坐标（ui，vi）（i＝1，2，3，…，n）和圆心坐标（uc，vc），利用线性最小二乘法求解式（1），便可得到纵横比μxy。

图1 标准模板圆的图像Fig.1 Image of standard circle

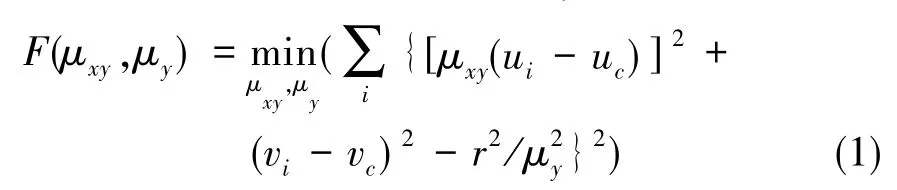
式（1）中，r为模板圆的半径，μy为CCD相机的像素在纵轴方向上的物理尺寸。

可变参数包括相机的内部参数和两相机之间的外部参数。本文采用平面模板标定法［11］，首先利用模板特征点之间的对应关系，经过图像数据的归一化处理，求解出平面模板和对应图像的单应性矩阵H。根据旋转矩阵的正交性和摄像机内部参数的约束条件，求出内部参数和外部参数的闭式解，也包括镜头的二阶径向畸变系数。最后，使用Levenberg⁃Marquardt非线性优化算法优化所有的标定参数。

2 相位光栅法及其三频外差原理

相位光栅法属于相位测量轮廓术，应用非常广泛。其基本原理是当使用DLP投射器投影编码光栅到被测物体表面时，投射光会受到物体表面形貌的调制而形成变形光栅，使用CCD相机接收已变形光栅的图像。如果投射光的强度满足标准正弦分布，则相机获取变形光栅的光强分布函数为

式（2）中，I（x，y）和A（x，y）分别为图像不同位置的光强和物体背景光强，B（x，y）为调制振幅，τ为条纹的频率，相位函数Δφ（x，y）表示变形光栅的相位变化，内含被测物体表面的三维信息。通过解调相位函数Δφ（x，y），便可以实现物体三维形貌的测量。目前，常用的解相方法包括相移法［12］和频域法，本文使用较为成熟的N步相移法。

N步相移法主要是在空域内对变形光栅图像进行处理，投射的正弦条纹每间隔一个固定的光栅周期1/N移动一次，同时产生对应的光强函数In（x，y），条纹的相位实际上移动了 2π/N。考虑到四步相移法能消除背景项和有效抑制测量系统非线性响应，同时投影条纹幅数也不是最多，故本文采用四步相移算法，每次相移量为π/2，所得到的4幅变形条纹的强度函数为

通过四步相移算法计算出的相位值被反正切函数截断在±π之间，导致在整个测量范围内每个像素的相对相位值不唯一。因此，必须对空间点的相位值进行展开以得到连续的相位分布，本文采用三频外差法来实现。

三频外差法结合了外差原理［13］和三频展开法［14］，将频率为 τ1、τ2和 τ3的相 位分布函数φ1（x，y）、φ2（x，y）和 φ3（x，y）分别投射到被测物体的表面，并依次同步拍摄得到对应的条纹图像。由四步相移算法得到三幅截断相位图，利用三次外差［15］，将每个点的相位沿时间轴独立的进行展开。外差其实就是对应像素点的相位之差，由此得到物体不同部位的绝对相位值，这样可从原理上避免误差的传播［16］。为了在整个测量范围内将相位准确的进行展开，应选择合适的τ1、τ2和τ3值，使得三次外差叠加最终得到条纹周期为1的相位图。

文中使用投射频率分别为 τ1＝1/70、τ2＝1/64和τ3＝1/59的三种光栅图像，经相移算法得到对应的相位分布函数Δφ1（x，y）、Δφ2（x，y）和Δφ3（x，y）。利用外差原理分别叠加Δφ1（x，y）和Δφ2（x，y）、Δφ2（x，y）和Δφ3（x，y），得到频率为τ12＝1/6和τ23＝1/5的相位Φ12和Φ23，然后再将Φ12和Φ23进行叠加，得到在整个测量范围内只有一个周期的相位Φ123，其频率τ123＝1，原理如图2所示。

图2 外差原理图Fig.2 Photograph of heterodyne principle

具体的展开过程为：定义展开运算符U［ϕ1，ϕ2］为

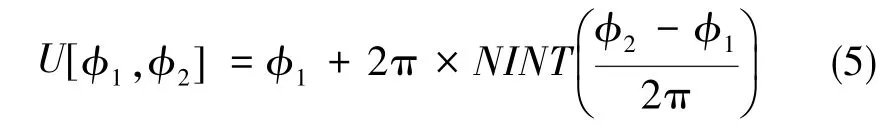
式（5）中，ϕ1和 ϕ2为相位，NINT（）为四舍五入算符，以频率τ123＝1的相位分布为基准，使用下面的公式进行展开

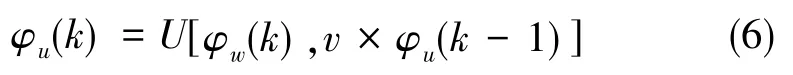
式（6）中，v为第k阶和第k-1阶之间的频率倍率，而k逐级取2、3。将展开的相位进行最小二乘法拟合，得到相位斜率为

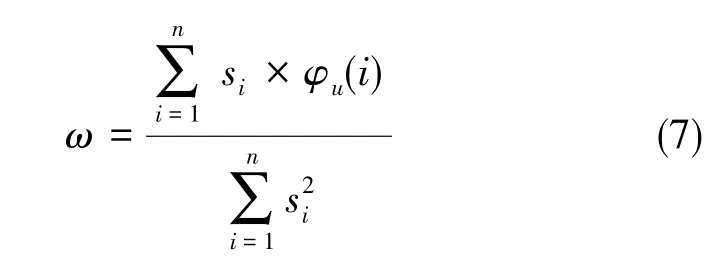
式（7）中，si为第 i阶的投影条纹数。将式（7）得到的结果乘以最大投影条纹数s，即可得到最终的展开相位ΔΦ

3 实验过程与测量结果

3.1 实验过程

测量系统如图3所示，主要包括投射系统、2组CCD相机及成像镜头、标定板、计算机和三脚架等硬件部分。投射系统使用的是ACER的基于DLP开发的数字投影仪，其亮度为1800lm（流明），投射分辨率为1024×1280。CCD相机及镜头是大恒的工业级相机和镜头，相机分辨率为1024×1280。镜头焦距为16mm。系统搭建完成之后，首先基于张正友的平面模板标定技术对系统的内部参数、外部参数和畸变参数进行标定，标定结果如表1所示。

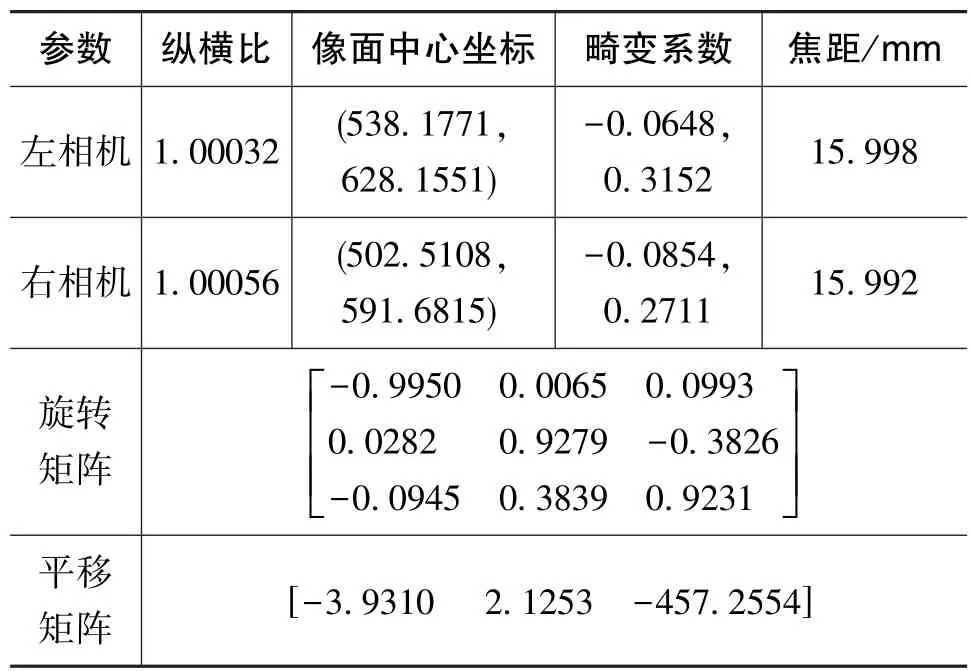
表1 测量系统的参数标定结果Table 1 Calibration results of measurement system

使用投影仪向被测物体投射先前设置好的3组（每组4幅）共12幅光栅条纹，由左右相机同步进行数据采集。利用第2部分介绍的四步相移和三频外差法计算被测物体各个位置像素的绝对相位，再结合双目视觉立体匹配中的极线约束和相位匹配技术［17］得到被测物体的三维点云数据。图4是CCD相机采集框架的部分条纹图像。

图4 采集的部分条纹图像Fig.4 Part of the strip images

要获取复杂异构体的全部三维信息，必须将多个视角的点云数据进行拼接。由于零件的运动属于刚性移动，因此可通过求取刚体运动的平移和旋转矩阵就可以实现拼接。本文采用文献［18］的方法在被测物体上粘贴圆形拼接点，在每个视角的重叠区域中设置至少3个拼接点，采用最小二乘法［19］对多个拼接点计算变换矩阵，并最终实现点云拼接。最后，将拼接的点云数据导入到Geomagic Studio三维软件中完成后续的点云数据处理、曲面重构和三维测量等工作。

3.2 测量结果

首先，验证系统的绝对测量精度。从检验部门获取了标准长度分别为100mm、80mm和55.12mm的3个量块，长度误差均为0.002mm。将得到的点云数据在Geomagic Studio软件中进行处理，采用最佳拟合方法求得各个量块的长度，实验结果如表2所示，图5是LK100的点云和三维模型结果。可见，本三维测量系统的绝对精度小于0.1mm。由于异构铸件的单边加工余量在2mm～3mm，因此系统能够满足尺寸检测的精度要求。

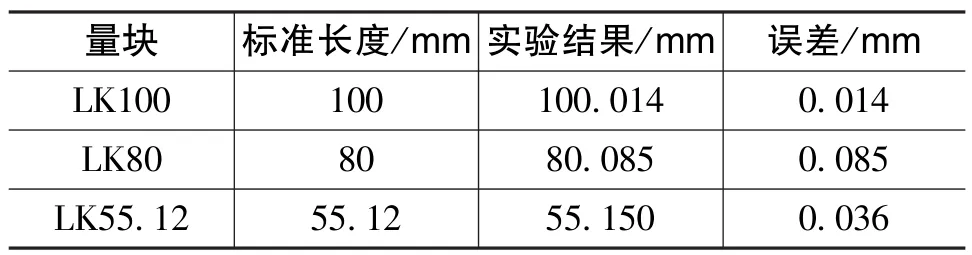
表2 标准量块测量结果Table 2 The results of standard board

图5 LK100的点云图和三维模型图Fig.5 Point cloud image and three-dimensional model image of LK100

验证完成系统的绝对测量精度之后，再对车间提供的某粗加工零件和结构铸件进行实物测量。在测量之前，先在零件表面粘贴拼接点，然后将零件放置在转盘上，每隔一定的角度旋转后进行扫描，旋转的角度务必保证任意相邻两个视角的重叠区域至少有3个拼接点出现。利用拼接点坐标信息将所有视角拍摄的图像进行拼接，最后根据刚体变换统一到一个坐标系下。同样将得到的点云数据在Geomagic Studio软件中进行处理，图6和图7分别是测量得到的粗加工零件和铸件的局部点云图和局部三维模型图。

采用最佳拟合的方法，以求取粗加工零件中圆孔的直径来说明系统对实物零件的测量结果。表3是粗加工零件正面和侧面圆孔直径的实际尺寸与系统测量结果比对表，实际尺寸由误差为0.01mm的卡尺获得，可见粗加工中各个圆孔直径的测量误差均在0.1mm以内。该粗加工从扫描到最终的三维尺寸输出用时在20min左右，另外铸件的测量用时在30min左右，明显提高了测量效率。

图6 粗加工零件的局部点云图和局部三维模型图Fig.6 Point cloud image and three-dimensional model image of rough machining

图7 铸件的局部点云图和局部三维模型图Fig.7 Point cloud image and three-dimensional model image of casting

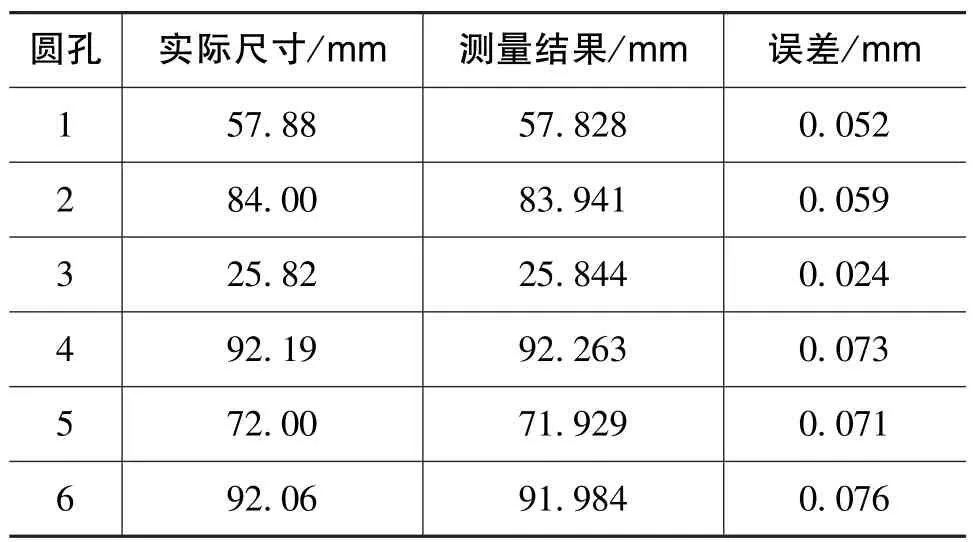
表3 粗加工零件圆孔直径的实际尺寸和系统测量结果Table 3 Real size and measurement results of the platform diameter

从对粗加工零件和铸件的测量结果来看，本系统有如下不足：1）光照不均匀和遮挡导致零件的有些区域尤其是内部区域无法实现测量，零件结构的复杂性增加了遮挡面积，在精度要求不高的情况下，可开发基于线结构光的便携式三维扫描系统。2）系统对表面光滑且反光的零件测量效果不佳，可通过对零件表面喷涂显影剂或者尝试使用新的投影技术来解决。3）系统单个视角的有效测量范围为200mm×200mm，基本满足现有铸件的三维测量需求，但不适合测量大于500mm的零件。4）目前，从点云处理到测量之间的过程均要通过专业的点云处理软件来完成，对测量效率有一定的影响。

4 结论

针对铸件的复杂多面体结构特点，基于双目视觉和光栅投影测量原理，搭建了一套异构铸件三维测量系统，验证了系统的绝对测量精度优于0.1mm，满足铸件测量的精度要求。对某粗加工零件和铸件进行了实物测量，得到了零件的三维点云和模型图，表明系统能够实现零件复杂表面形貌的三维尺寸测量，具有较高的测量效率。本系统有望替代现有人工划线的测量方式，同时本文的研究工作可为航天复杂多面体零件以及未来大型结构件的三维检测提供参考和借鉴。另外，系统也有自身的不足之处，实验过程存在系统误差，导致测量结果和准确值有一定偏差，后续应该通过提高硬件配置、采用新的投影技术、优化标定算法和流程等工作，最终进一步提高测量准确性。