障碍地形下的机器人轮足复合越障步态规划方法
2019-02-10张世俊
张世俊,邢 琰,2,胡 勇,2
(1.北京控制工程研究所,北京100190;2.空间智能控制技术重点实验室,北京100190)
0 引言
地面移动机器人的运动方式主要包括轮式、足式和履带式等。其中,轮式机器人在硬平地面上的移动速度快,具有较好的稳定性,但是其在障碍地形中的运动能力不够理想;足式机器人在平地上的运动效率较低,但由于其可利用非连续地面实现支撑,且支撑点可达的空间范围大,因而对各种复杂地形情况的适应能力也较强。轮足复合机器人结合了两者的优点,兼顾了运动高效能与环境适应性,在机器人移动过程中不仅可根据需要在轮式与足式两种运动模式之间切换,而且可采用轮足复合运动模式[1⁃2]。
当机器人采用足式运动模式通过障碍地形时,步态规划是其运动规划与控制中的核心内容,包括决策各腿运动时序、合理选择落足点、规划足端轨迹与机体运动轨迹等部分。针对上述几个方面的内容,已有许多研究成果。文献[3]通过深入研究机器人机体运动对足端可达空间的影响,提出了一种自由步态算法,利用机器人机体位姿的调整尽可能地增大了寻找有效落足点的概率,从而提高了机器人克服障碍地形的能力;文献[4]针对四足机器人提出了一种基于A∗算法的自由步态规划方法,使机器人以较少的步数安全地通过了给定的含障碍物的地形;文献[5]综合考虑了机器人的稳定性与行走速度,提出了一种自由步态生成算法,使得机器人可自主通过具有有限落足点的地形。通过分析已有的理论结果可知,采用纯足式运动的机器人虽然可以顺利通过障碍地形,但在跨越障碍时需进行大量的步态调整,导致机器人的通行效率降低。目前,障碍地形下的轮足复合机器人步态规划方法主要是根据地形环境,在轮式运动与足式运动之间切换[6⁃7]。
而在步态规划中,结合轮足复合运动模式能有效降低运动能耗,提高通行效率。轮足复合运动模式主要可分为以下三种形式:主动关节被动轮模式[8⁃9]、被动关节主动轮模式[10⁃11]和主动关节主动轮模式。目前,针对主动关节与主动轮模式的运动控制研究相对较少,其在运动规划与控制中需协调各腿关节摆动与各轮转动,文献[12]~文献[15]分别针对不同结构的轮足复合机器人提出了相应的运动控制方法,实现了机器人在连续崎岖地面上的通行能力,但并未针对不连续地形的越障步态进行研究。
为提高机器人的适应性,更快更稳地穿越障碍地形,本文提出了一种轮足复合越障步态规划方法。每个步态周期包括位姿调整阶段和迈步阶段两部分,其中在位姿调整阶段采用轮足复合运动模式,与纯足式步态越障方式相比具有较高的通行效率。首先,根据机器人当前的状态与地形信息,提出了一种轮足复合机器人位姿调整算法,包括机器人整体位置调整算法、重心位置调整算法和支撑腿相对位置调整算法。其次,基于轮足复合运动的运动学方程,给出了位姿调整阶段的轮速规划算法,使得每条腿足端轮子的滚动速度与足端的轨迹相匹配,可确保轮子在地面滚动时不发生滑动。最后,虚拟样机仿真结果表明,应用本文提出的步态规划算法,机器人能够自主平稳地穿越障碍地形,从而验证了本文方法的有效性。
1 轮足复合越障步态规划算法框架
对于障碍地形下的轮足复合机器人运动规划,当遇到轮式运动无法通过的障碍时,需要采用合理的足式或轮足复合运动模式跨越障碍。足式运动一般采用自由步态算法,在线决策迈腿顺序、摆动腿的立足点及足端运动轨迹。针对实际的障碍地形,由于地形的限制,往往需要插入一定的调整步态,在每一次迈步前需要规划调整机器人的位置姿态,机器人调整至适合迈步的状态。其中,包括调整机器人位置使得机器人靠近障碍,调整机器人重心和支撑三角形,使得摆动腿的足端工作空间覆盖障碍,并且保证机器人的重心在迈步过程中保持在支持三角形区域内。
如图1(a)所示,机器人需要跨越前方的一个沟壑。规划右前腿的下一落足点为P1,由图中可知右前腿的足端工作空间没有覆盖落足点P1,因此机器人在当前状态下不能摆动右前腿跨越沟壑,需要先调整机身使得右前腿的足端工作空间向前移动ΔH。而在当前状态下,机器人重心前移ΔH后处于支撑区域之外,因此需要先向前迈右后腿,以保证身体在重心前移后仍处于稳定支撑三角区域内,如图1(b)所示。


图1 足式运动越障迈步示意图Fig.1 Illustration of obstacle negotiating gait with legged movement mode
根据上述分析可知,由于地形障碍的限制,机器人在迈右前腿跨越障碍时,需要先进行迈右后腿和重心调整两个步骤。本文提出了一种轮足复合越障步态规划方法,采用轮足复合运动模式实现机器人迈步前的位姿调整,同时进行机器人整体位置调整、重心调整和支撑腿相对位置调整,与纯足式步态越障相比,大大节约了通过障碍地形的时间。轮足复合越障步态规划方法可由图2所示的状态向量机表示,第一部分为运动规划阶段,规划出了机器人当前步态周期的位姿调整运动和迈步运动;第二部分为位姿调整阶段,此阶段采用轮足复合运动模式,同时进行机器人整体位置调整、重心调整和支撑腿相对位置调整,将机器人调整至适合迈步的状态;第三部分为迈步阶段,机器人根据规划的摆动腿轨迹迈腿至规划的落足点,算法流程图如图3所示。
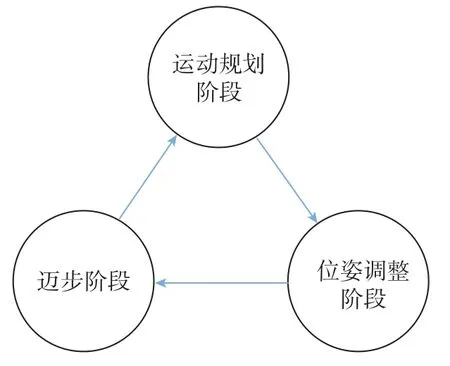
图2 一个迈步周期内的状态机Fig.2 State machine within a stride cycle
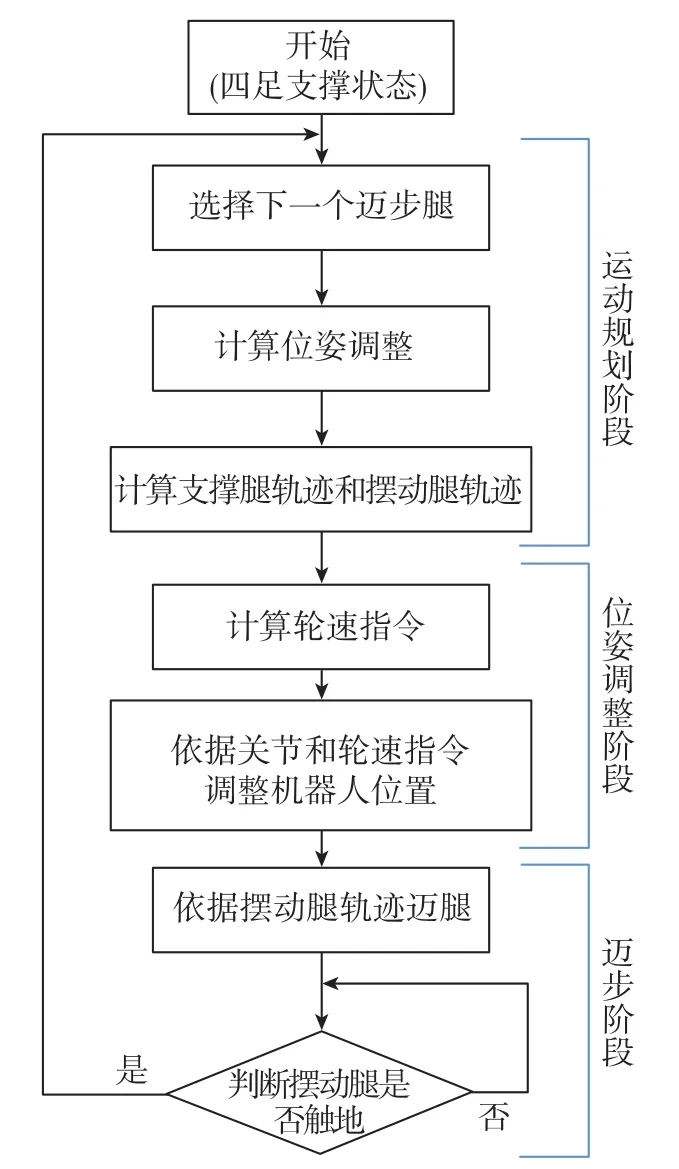
图3 轮足复合越障步态规划的算法流程图Fig.3 Flow chart of proposed wheel-legged obstacle negotiating gait planning algorithm
2 机器人位姿调整算法
为简化位姿调整规划算法,将其分解为三部分进行调整:机器人整体位置的调整、机器人重心位置的调整和支撑腿相对位置的调整。将每部分进行独立规划,最后经过运动合成实现机器人的整体位姿调整运动,本文将在本节后续的小节中分别介绍这三部分算法。
本文研究的轮足复合机器人的总体构型如图4所示,机器人包含4条腿,每条腿具有3个关节,分别为根关节(偏航自由度)、髋关节(俯仰自由度)和膝关节(俯仰自由度),每条腿末端装有独立驱动的轮子,可根据需要在轮式运动方式和足式运动方式之间进行切换。为方便描述,将机器人的四条腿按左前腿、右前腿、左后腿、右后腿的顺序进行编号,分别为腿1、腿2、腿3、腿4。
首先,建立如图4所示的三个坐标系。世界坐标系Σw为机器人运动过程的参考坐标系,固定于地面;机器人本体坐标系Σb固连于机器人身体,其原点位于机器人身体中心,x轴指向机器人右方,y轴指向机器人正前方,z轴垂直于机器人身体并且向上;导航坐标系Σn的原点为每个运动规划阶段中机器人身体中心在地面上的投影点,z轴垂直向上,y轴水平指向机器人前进方向,x轴水平向右且满足右手坐标系法则。
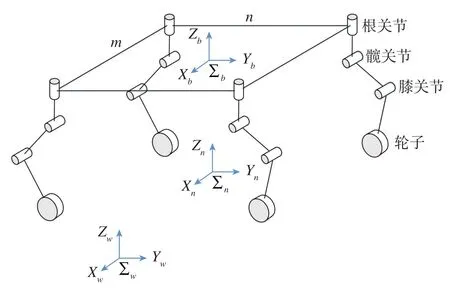
图4 轮足复合机器人的结构示意图Fig.4 Structure of wheel-legged robot
2.1 机器人整体位置调整
为提高机器人的越障效率,使机器人在越障前靠近障碍,计算机器人整体移动的距离
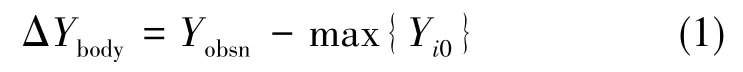
式(1)中,Yobsn为导航坐标系下障碍近端的y轴坐标,Yi0为导航坐标系下机器人未跨越障碍的腿中第i条腿足端的y轴坐标。
2.2 机器人重心位置调整
当机器人在当前状态下不能直接通过迈腿实现障碍跨越时,需要先调整重心使得迈步腿的足端工作空间向前移动并覆盖障碍地形。因此,需要计算机器人在当前状态下各足端的可达区域,足端的可达区域为足端工作空间与地面的相交区域,而机器人的站立高度不同,足端的可达区域也不同,图5说明了机器人身体的高度hd对足端可达区域的影响。机身纵向平面内的足端工作空间由四段圆弧围成,足端可达区域可被分为如下两种情况。当hd<h1时,具有如下关系
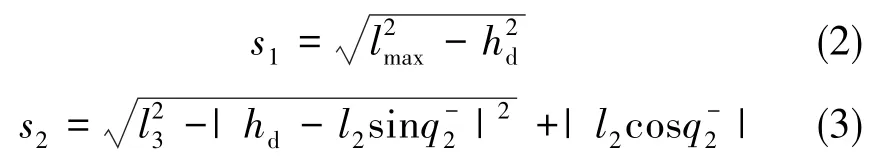
当hd>h1时,关系如下

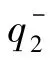

由图5可以看出,机器人身体高度越低,摆动腿的可达区域越大,即机器人的最大迈步步长越大,而摆动腿的越障高度越低。在正常情况下,机器人的身体姿态保持水平,机器人行走高度设定在合适高度,使得机器人的迈步步长和越障高度较为均衡。当机器人要跨越较宽的沟壑时,需要降低机器人身体的高度,以获得更大的迈步步长;当机器人要跨越较高的障碍时,需要增大机器人身体的高度,以获得更大的抬升距离。
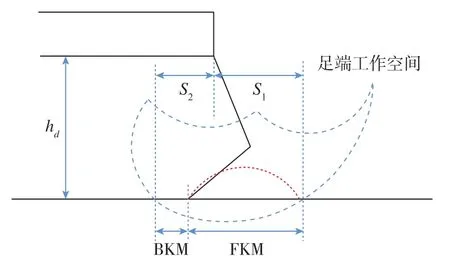
图5 机器人身体重心高度对摆动腿可达区域的影响Fig.5 Influence of robot body gravity height on the reachable area of swinging leg
本文进一步给出了如下两个概念[16]。前向运动学裕度 (FKM)是指机器人在当前状态下,某条腿在地面上沿机器人前进方向可运动的最远距离在水平方向上的投影;后向运动学裕度(BKM)是指机器人在当前状态下,某条腿在地面上沿机器人前进反方向可运动的最远距离在水平方向上的投影。如图5所示,FKM与BKM可由当前足端位置与足端可达区域求得。
机器人重心位置调整算法的基本原则为通过调整机器人的机身,使得在机器人前进方向上摆动腿的可达空间覆盖下一个落足点,即下一个迈步腿的FKM覆盖跨越障碍后的落足点,如图1所示。由此可计算出机器人重心调整的距离

式(7)中,Yobsf为导航坐标系下障碍远端的y轴坐标,Yi0为导航坐标系下机器人下一迈步腿i的足端y轴坐标,FKMi为迈步腿i的前向运动学裕度,ΔYbody为机器人的整体调整距离。
机器人重心位置的调整同时需要满足后向运动学裕度约束,机器人身体向前进方向调整的距离等于支撑腿相对于身体向前进反方向移动的距离。因此,机器人身体调整的范围为最小后向运动学裕度

式(8)中,BKMi为第i条腿的后向运动学裕度。
2.3 支撑腿相对位置调整算法
上一小节给出了机器人重心位置的调整距离,为保证机器人在迈步时的静稳定性约束条件,机器人在行走时需保持重心的水平投影位于支撑多边形内,并满足一定的稳定裕度,由此可计算出支撑腿的调整位置。本文忽略了腿部质量对机器人重心的影响,假设机器人重心与机身中心重合,采用纵向稳定裕度(LSM)分析静态稳定性[17],即机器人机体重心投影点沿机体前进方向距离前后支撑边界的距离,分别为前纵向稳定裕度(FLSM)和后纵向稳定裕度(BLSM),如图6所示。
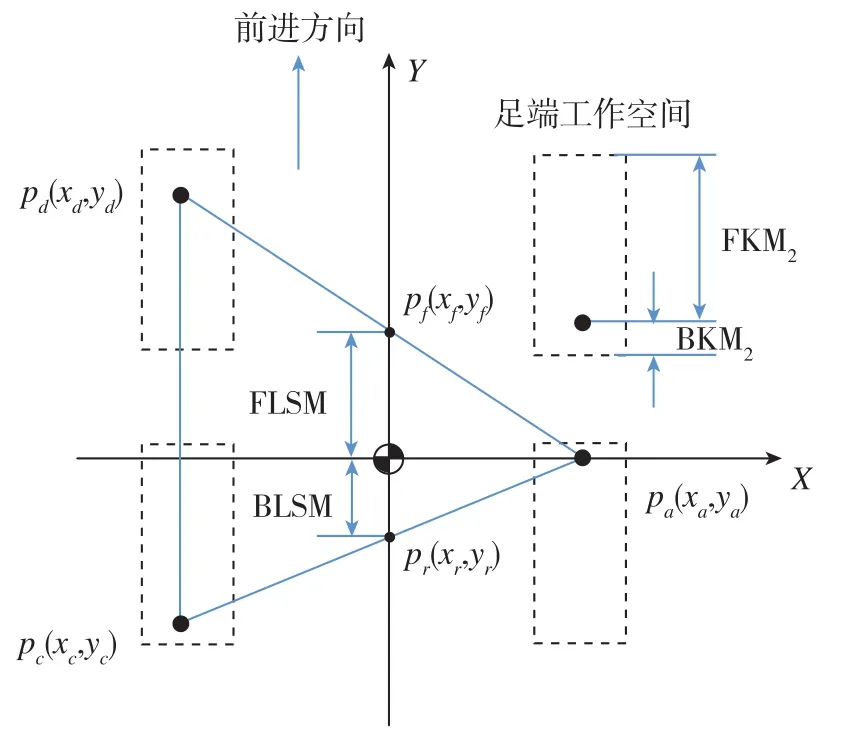
图6 机器人支持区域水平面投影Fig.6 Horizontal projection of robot supported regional
迈步时的支撑区域可用由三个支撑足端连线组成的三角形来描述。为描述方便,在本小节对机器人的四条腿重新进行编号,令下一迈步腿在导航坐标系Σn中xy平面内的投影坐标为pe(xe,ye),与迈步腿同侧的足端投影坐标为 pa(xa,ya),迈步腿对侧的前足和后足的投影坐标分别为pd(xd,yd)、pc(xc,yc),如图 6 所示。假设根关节不发生偏转,每条腿仅在机身纵向平面内摆动,调整与下一迈步腿同侧的支撑腿使得FLSM与BLSM相等,此时机器人具有最大纵向稳定裕度。前后支撑边界与y轴的交点坐标为
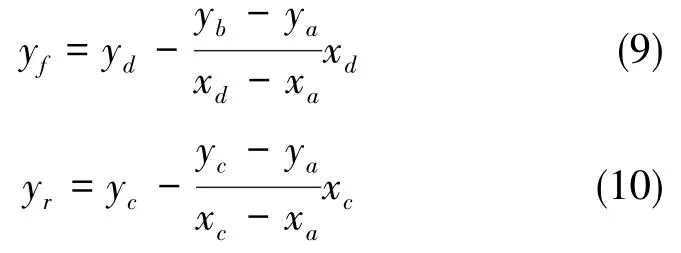
由yf=-yr可得,与下一迈步腿同侧的支撑腿足端坐标 pa(xa,ya)满足
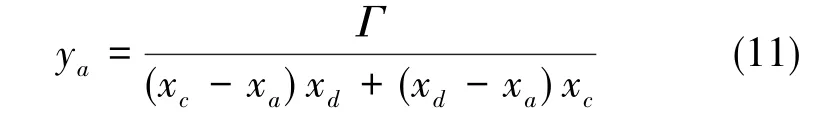
式(11)中,Γ=(xc-xa)ydxd+ (xd-xa)ycxc-(xd-xa)(xc-xa)(yc+ yd),若下一迈步腿为左侧腿,则 xa=-m/2、xd=m/2、xc=m/2; 若下一迈步腿为右侧腿,则 xa=m/2、xd=-m/2、xc=-m/2,m为机器人身宽。由此可计算出支撑腿的调整位置,进而可求得支撑腿需调整的距离
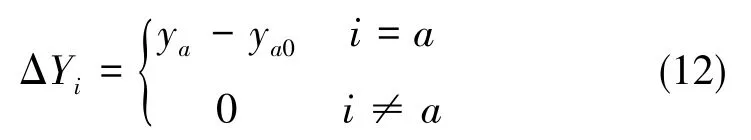
式(12)中,ya0为运动规划阶段足端a在导航坐标系y轴上的投影坐标,i=a,c,d,e。
2.4 轨迹方程
前三个小节分别给出了机器人整体位置的调整算法、机器人重心位置的调整算法和支撑腿相对位置的调整算法。由此可得机器人位姿调整阶段各支撑腿在本体系下的调整距离
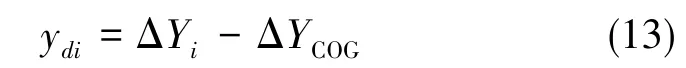
本体系下足端运动轨迹方程由如下一个五次多项式形式描述[5]
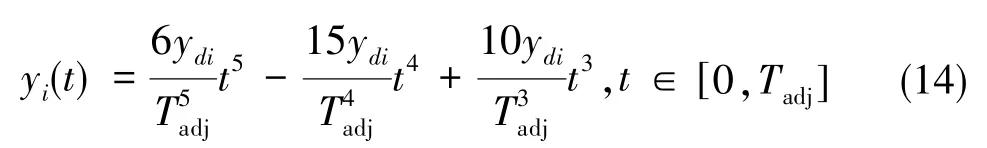
式(14)中,Tadj为机器人位姿调整的时间,ydi为第i条腿的调整距离。该轨迹方程能够保证机器人位姿调整的连续光滑性,并且满足初始和末尾时刻的速度与加速度为0,进而根据逆运动学方程求得关节角曲线。
同理,位姿调整阶段机器人机身在世界系下的调整距离为
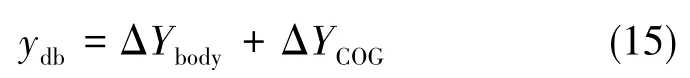
机身轨迹方程同样由一个五次多项式形式描述
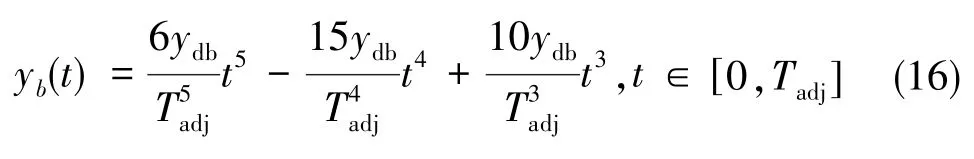
3 轮速规划算法
在轮足复合运动模式中,机器人的四条腿始终接触地面进行位姿调整,各腿依据规划的轨迹方程沿地面运动。与此同时,每条腿末端的轮子绕足端转动,每条腿足端轮子的滚动速度应与足端的轨迹相匹配,以确保轮子在地面滚动时不发生滑动。
建立轮地接触点坐标系Σci,如图7所示。
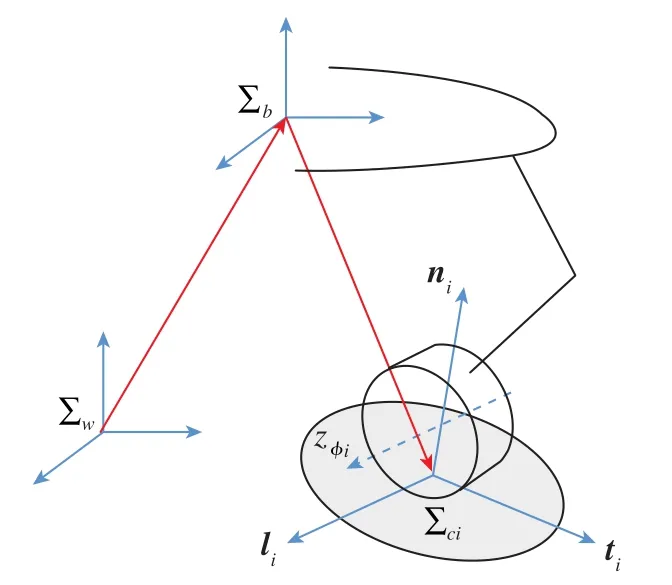
图7 接触点坐标系示意图Fig.7 Illustration of the contact point coordinate system
图7中,ni为接触点法向单位矢量,ti为纵向单位矢量,li=ti×ni为横向单位矢量。本文中,假设在采用轮足复合运动时地面为刚性平地,则有ni=[0 0 1]T,ti可由下式计算
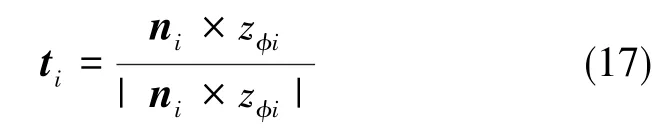
式(17)中,zϕi为轮子旋转轴向量。假设轮上Q点与轮地接触点相重合,由运动学方程有
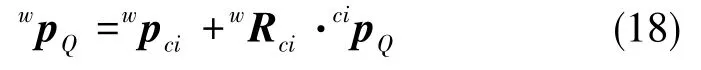
式(18)中,wpQ为世界坐标系下轮地接触点向量,cipQ为轮地接触点坐标系下轮地接触点向量,wRci为世界坐标系到轮地接触点坐标系的转换矩阵,wpci为世界坐标系下轮地接触点坐标系原点向量。对式(18)求导可得
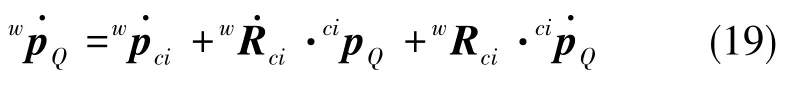
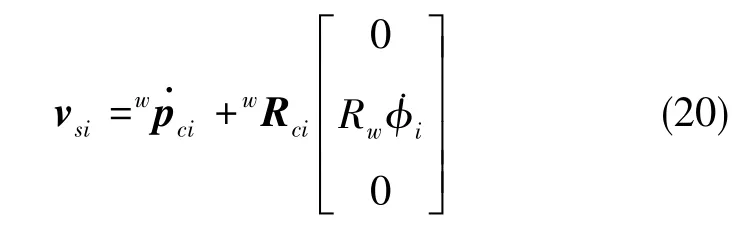
式(20)中,vsi为第 i个轮子的滑动速度,Rw为轮子半径,̇ϕi为轮子转速。转换矩阵wRci=[litini],如图 7 所示。
由机器人正运动学可知
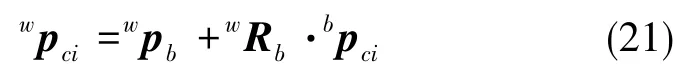
式(21)中,wpb为世界坐标系下机身坐标系原点向量,wRb为世界坐标系到机器人本体坐标系的转换矩阵,bpci为机器人本体坐标系下轮地接触点向量,对式(21)求导可得

式(22)中,

式(23)中,wωb为机身角速度向量。
将式(22)带入式(20),可得

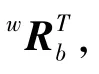

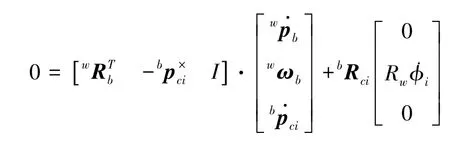
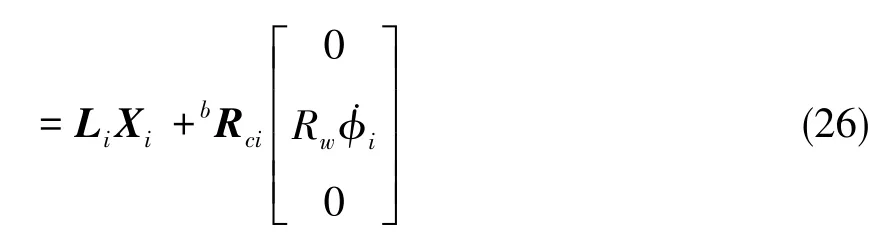
4 迈步规划算法
4.1 迈步顺序
自然地形下的足式运动步态规划一般采用自由步态算法,在线决策迈腿顺序,并且在每一次迈步前需要调整稳定支撑区域,使得机器人身体重心可被调整到合适迈步的位置。
采用本文提出的轮足复合越障步态规划方法,在机器人位姿调整阶段可同时进行机器人整体位置调整、重心位置调整和支撑腿相对位置调整,因此迈腿顺序的选择可完全基于机器人越障目标,可简化机器人跨越障碍的迈步过程。为缩小机器人的调整范围,优先选择靠近障碍的腿为下一迈步腿。机器人在跨越障碍的过程中,始终在轮足复合运动模式与迈腿模式之间轮流交替,具体迈步腿的选择算法逻辑图如图8所示。
4.2 摆动腿轨迹
当已知地形信息、摆动腿当前的足端位置和落足点后,世界坐标系下摆动腿轨迹采用一种矩形曲线,保证机器人在迈腿过程中不与障碍发生碰撞。轨迹由三段直线段组成,分别为垂直抬起、水平前移和垂直落下三个阶段,如图9所示。图中实心正方形为摆动腿足端初始位置,实心圆为摆动腿足端末端位置,虚线为足端轨迹。每个直线段采用形式与式(14)相同的轨迹方程,进而根据式(21)可求得本体系下摆动腿足端轨迹方程。
5 虚拟样机仿真
在Adams中搭建四足机器人虚拟样机模型,采用Adams和Simulink联合仿真技术进行虚拟样机仿真。机器人的总质量为200kg,大腿长度为0.4m,小腿长度为0.3m,轮子半径为0.1m。为验证本文提出的轮足复合越障步态规划方法的有效性和机器人通过障碍地形的能力,本文分别对沟壑类和台阶类两种地形进行了仿真。
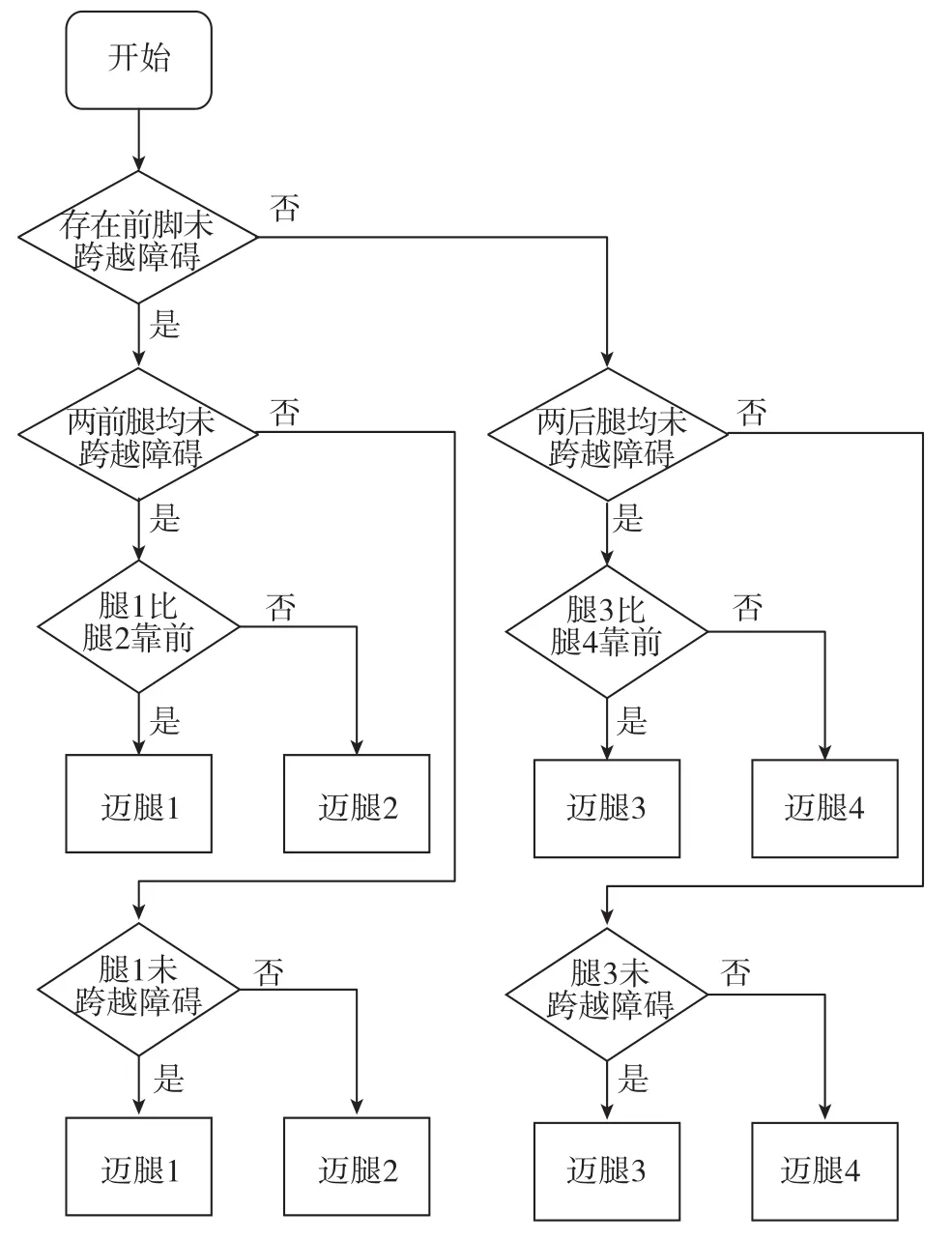
图8 迈步算法逻辑图Fig.8 Logic diagram of step algorithms

图9 摆动腿足端轨迹Fig.9 Foot trajectory of the swinging leg
图10为机器人通过沟壑类障碍地形的仿真截图,沟壑的宽度为0.4m。图11为机器人通过台阶类障碍地形的仿真截图,台阶的高度为0.2m。两种地形障碍近端距离机器人中心的距离均为1.5m,机器人能够自主、平稳地通过障碍地形。
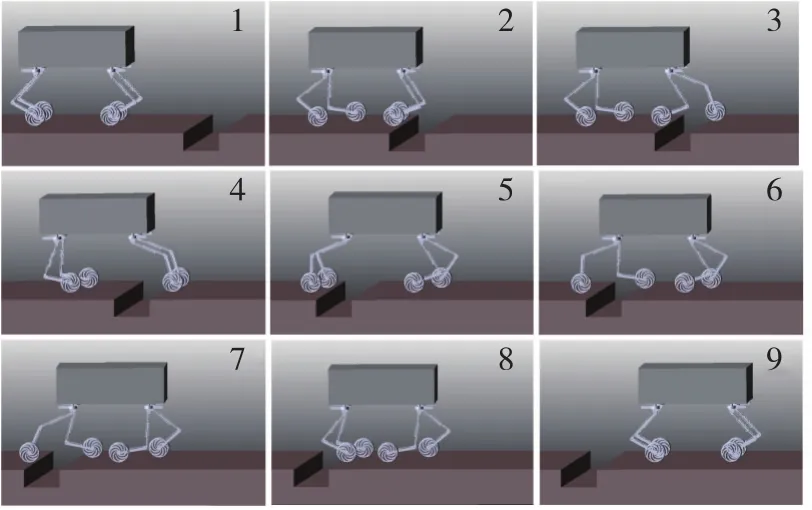
图10 沟壑类障碍地形仿真截图Fig.10 Snapshots of the simulation under gully terrain
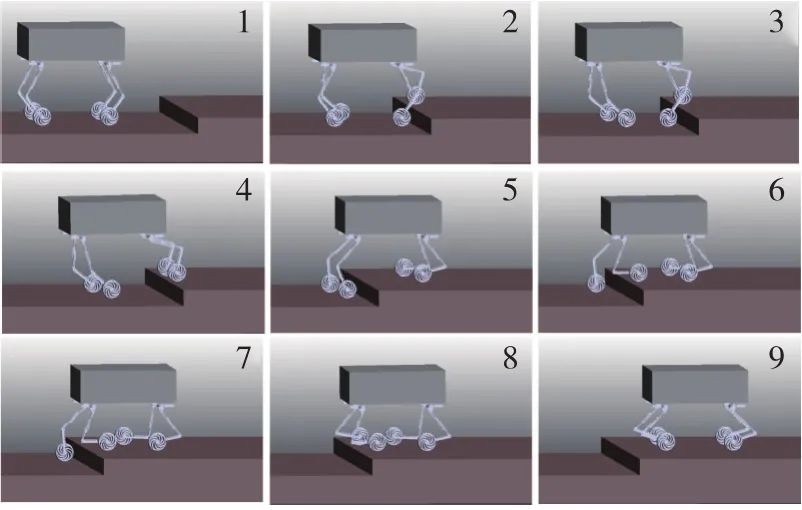
图11 台阶类障碍地形仿真截图Fig.11 Snapshots of the simulation under step terrain
图12和图13分别为沟壑类与台阶类地形下机器人身体中心在前进方向上的移动轨迹,机器人的移动轨迹连续且重心一直向前运动,有效提高了机器人通过障碍地形的效率。
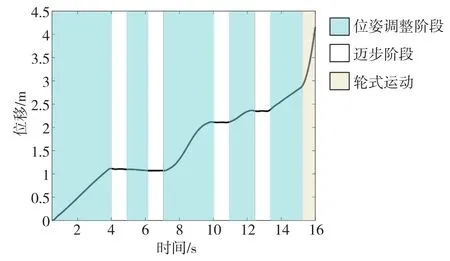
图12 沟壑类障碍地形下机器人身体中心在前进方向上的移动轨迹Fig.12 Robot forward position curves under gully terrain
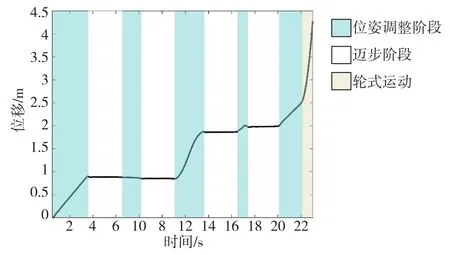
图13 台阶类障碍地形下机器人身体中心在前进方向上的移动轨迹Fig.13 Robot forward position curves under step terrain
图14和图15分别为沟壑类与台阶类地形下机器人身体的俯仰角与滚转角曲线,机器人在通过障碍地形时的机器姿态波动被控制在2°以内,步态较为平稳。
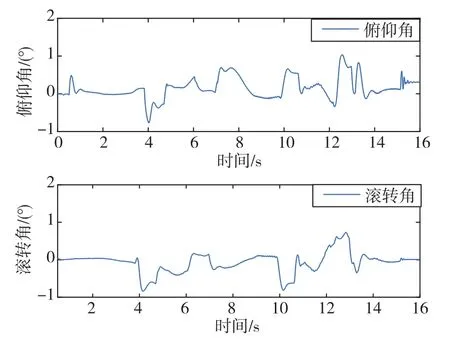
图14 沟壑类障碍地形下机器人的机身姿态角曲线Fig.14 Body attitude angle curves under gully terrain
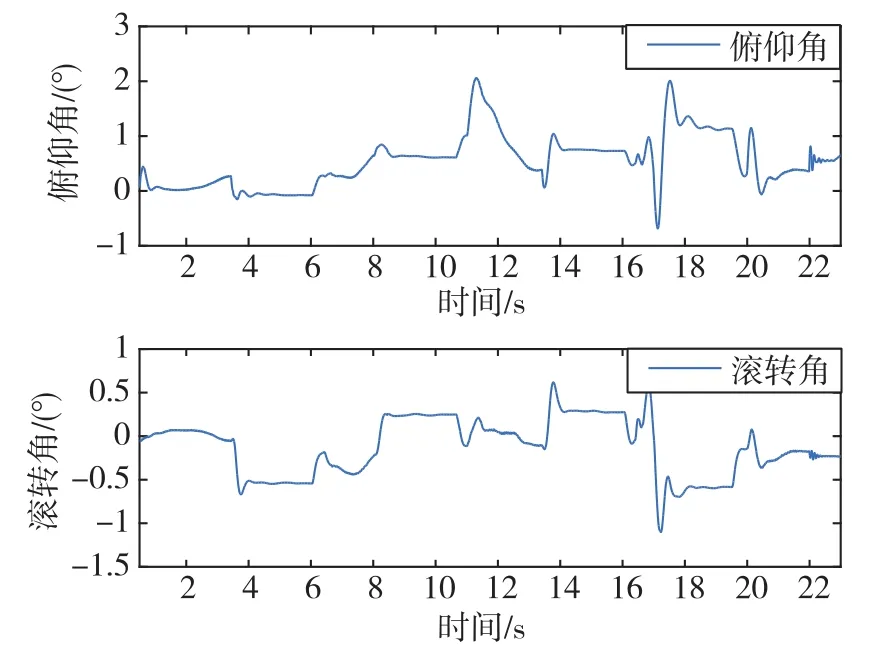
图15 台阶类障碍地形下机器人的机身姿态角曲线Fig.15 Body attitude angle curves under step terrain
6 结论
本文针对具有大障碍的地形情况,提出了一种轮足复合越障步态规划方法,将每个步态周期分为位姿调整阶段和迈步阶段两部分。其中,位姿调整阶段采用轮足复合运动模式,与纯足式步态越障相比具有更高的通行效率。
轮足复合运动模式根据机器人的当前状态与地形信息,同时进行机器人整体位置调整、重心位置调整和支撑腿相对位置调整,将机器人调整到适合迈步跨越障碍的状态。进而基于轮足复合运动的运动学方程,给出位姿调整阶段的轮速规划算法,使得每条腿足端轮子的滚动速度与足端的轨迹相匹配,可确保轮子在地面滚动时不发生滑动。
最后,针对沟壑与台阶类地形进行虚拟样机仿真,结果表明应用本文提出的轮足复合越障步态规划算法,机器人成功地通过了障碍地形,姿态波动平稳,从而验证了本文方法的有效性。
