基于因子图的卫星拒止环境下的多信息融合技术

徐 璟，杨功流，孙艺丁

（北京航空航天大学仪器科学与光电工程学院，北京100191）

0 引言

目前，以GPS为代表的卫星导航系统已成为现代军事、民用导航的重要信息基础设施。但是，卫星导航信号难以穿透地面和建筑物等密度较大的物质，在都市、室内、地下等环境中信号的衰减现象非常严重［1］。针对卫星导航在一些特定条件和环境下应用的局限性，国内外均对卫星信号拒止环境下的新导航技术开展了多项研究，其中就包括了基于因子图的导航定位技术。

2012年，美国Georgia理工学院的Indelman等针对美国国防高级研究计划局（DARPA）提出的全源定位导航项目，参照Dellaert［2］等的SAM系列算法和一些平滑定位新算法［3⁃7］，提出了基于因子图（Factor Graph，FG）框架的多源导航传感器融合方法［8⁃10］。2013 年，美国 SRI 国际公司的 Chiu 等［11］在美国Georgia理工学院的研究基础上，针对机器人自主导航问题给出了基于因子图的组合导航系统，该系统包括57种不同的传感器。2013年，德国Chemnitz工业大学的Lange等［12］将基于因子图框架的增量平滑多源导航传感器融合方法应用到装配有惯性测量单元、光流传感器和无线电高度表的四旋翼无人机中，并与传统的扩展Kalman滤波（Extended Kalman Filter，EKF）方法及其变体方法作对比，仿真实验和物理实验结果证明基于因子图的增量平滑方法比传统滤波方法更具有优势。2015年，西北工业大学的戚丽萍［13］开展了基于因子图的INS/GPS/VO组合导航方法研究，给出了因子图框架下INS/GPS/VO组合导航系统的算法流程，采用固定滞后平滑优化的方法对该组合导航系统进行优化求解，并在不同导航数据更新频率和不同导航传感器组合模式下完成了仿真试验。

综上所述，国外已经展开了基于因子图框架的多源数据融合方法，并且能够较好地处理异步、多速率数据，但是算法的应用背景多以小场景、低动态的SLAM问题为主，还未在大场景下进行过验证。国内虽然也展开了该技术的研究，但都以无人机为应用背景，且以仿真试验居多，没有在实地大场景下进行过验证。本文利用因子图框架对不同频率的传感器量测信息进行融合，通过因子节点的增加和删减来实现多传感器即插即用，实地车载实验验证了所用算法的有效性。

1 因子图概论

“因子图”实际上是一种概率图模型，其应用广泛，不仅可以用来解决数学概率问题，还被用来解决人工智能、信号处理、数字通信等其他领域的复杂问题［10，14⁃15］。

因子图指的是将一个具有多个变量的全局函数因子分解成几个局部函数的积而形成的一个二分图模型G＝（F，Θ，ε），其中包含变量节点θj∈Θ、因子节点 fi∈ F 和连线 eij∈ ε［16］。设 g（θ1，θ2，θ3，θ4）是具有4个变量的全局函数，将其分解成3个局部函数f1、f2、f3之积，即

式（1）对应的因子图如图1所示。在图1中，每个变量对应一个变量节点，每个局部函数对应一个因子节点，因子图的边线由变量节点和因子节点的连线组成。当且仅当因子图中变量节点θj是局部函数fi的自变量时，它们之间才会有一条连线eij连接。

图1 因子图示例Fig.1 Example of factor graph

2 基于因子图的多传感器融合设计

2.1 融和原理

基于因子图的信息融合算法的基本思想是：通过构建某一时间段内的因子图模型，将系统状态与导航信息相关联，再基于后验估计理论实现数据的融合。即在给定所有可用量测值后，计算所有状态的联合概率分布函数的最大后验概率估计（MAP）［17⁃18］，如下所示

因式分解可将 p（X0∶k｜Z1∶k）分解为多个局部函数之积，如下所示

2.2 各传感器量测模型及因子

现代组合导航系统中包含有多种传感器，针对其不同的量测模型需提出不同的因子节点配置。下面对之后试验中包含的几类传感器列出其因子节点表达式。

（1）惯组（IMU）量测因子

在惯导系统中，导航状态x的时间更新可以用如下方程描述

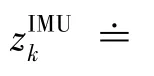
这种预测与状态xk估计之间的差别就是因子节点中所代表的误差函数，即

由式（8）可以看出，IMU量测因子与相邻时刻的导航状态相关。

（2）北斗卫星导航系统（BDS）量测因子

BDS量测方程可以表示为

式（9）中，nBDS为量测噪声，hBDS为量测函数，由上述量测方程可以定义BDS量测因子

由式（10）可以看出，BDS因子只与当前时刻的导航状态有关。Baro⁃altimeter（气压高度计）的量测因子可参考BDS量测因子的定义。

（3）里程计量测因子

对各类传感器的量测因子进行定义后，就可以得到导航系统信息融合的因子图框架，如图2所示。其中，IMU、BDS、高度计和里程计的频率分别为100Hz、1Hz、5Hz和1Hz。

图2 基于因子图的多传感器融合框架Fig.2 Multi-sensor fusion framework based on factor graph

由图2可知，基于因子图的多传感器信息融合方法可以对不同频率、不同线性特征的传感器数据进行融合处理。当导航系统接收到新的传感器输出数据时，在因子图框架上扩充变量节点及相应的因子节点。而当某传感器失效时，在因子图中不再添加该传感器的量测因子节点即可。而对于基于传统Kalman滤波的多源融合方法，当导航系统中新加入一种导航传感器时，滤波器的框架需要进行一定的修改。如联邦滤波器的主滤波器中全局估计的协方差阵需要重新计算，这使得联邦滤波器需要一段时间来进行结构的调整以适应新的导航传感器量测信息输入。

因此，基于因子图的多传感器信息融合方法可以实现导航系统中传感器信息的即插即用，便于载体在卫星拒止环境下快速有效地进行系统状态的更新，保证载体的导航定位精度。

3 试验验证

采用实地跑车试验对文中提出的方法在卫星拒止环境下进行分析验证，试验车辆装有IMU、北斗卫星信号接收仪、气压高度计和里程计，如图3所示。各传感器的更新率、零偏及观测误差如表1所示。

表1 传感器更新率及误差Table 1 Update frequencies and errors of the sensors

图3 车载导航系统实物图Fig.3 Structure of the ground vehicle navigation system

车载试验全程为27383m，总时长为1359s。由于试验前半段路程为直线行驶，其结果不能很好地说明本文提出的方法的有效性。本文选择含有几段转弯的后半段跑车试验来进行分析验证，时间范围为750s～1350s。在后半段跑车试验中，令5个时间段内北斗卫星信号消失，消失时间段的始末时间如表2所示。

表2 北斗卫星信号消失始末时间Table 2 Signal disappearance beginning and end time of the Beidou satellite

跑车试验结果在谷歌地图上的显示如图4所示。从局部放大图中可以看出，在开始的100s内，基于因子图融合的导航路线误差较明显。这是因为算法中将载体初始速度设为静止，而载体真实速度并不为零所致。但在之后的试验过程中，因子图融合路线与真实路线重合度高，其位置误差曲线如图5所示。由于东向和北向位置误差在前100s内较大，为了便于观测，将850s以后的位置误差结果显示在图5中。

图4 因子图融合曲线与真实路线对比图Fig.4 Trajectories of the proposed method and the ground truth

图5 基于因子图的导航系统位置误差曲线Fig.5 Position error curves of the integrated navigation system

由图5可知，试验车辆经过600s行驶后，在位置误差方面，东向和北向的误差在10m以内，高度误差在6m以内。总体来说，试验车辆在导航卫星信号变更的情况下，导航精度依旧可以得到有效保障。因此，本文提出的基于因子图的多传感器信息融合方法能在卫星信号拒止环境下将剩余传感器信息进行快速有效融合，实现多传感器信息即插即用，确保载体的导航精度。

4 结论

本文针对现有载体导航系统多依赖卫星信号，而卫星信号在特定环境中容易失效导致系统导航精度下降的问题，提出了一种基于因子图的多传感器信息融合方法。首先介绍了因子图的原理，并通过各传感器的量测方程得到导航系统信息融合的因子图框架。实地跑车试验结果表明，该方法能在卫星拒止环境下实现多传感器信息的快速有效融合，确保载体导航精度。