自适应非负矩阵分解的人脸识别方法研究

覃阳 肖化

摘要：在单样本或者小样本的人脸识别系统中，常常会面临样本数量不足的问题，为解决少样本情况下的分类精度，以及利用原始特征或者目标特点重构的虚拟样本过于单一等问题，提出一种自适应非负矩阵分解（NMF）的人脸识别方法。该方法首先在矩阵分解过程中构造不同矩阵维度和迭代次数参数下的重构样本;然后利用QR分解稀疏表示方法进行人脸分类;最后，通过选取最优参数组合，调整重构样本，直至达到最佳分类效果。在ORL、Yale和AR3个数据库上的实验结果表明，该算法在最佳参数下，尤其是单样本情况下对比基于原样本方法的准确率平均提高了约5%，最高提高了约10%～15%。

关键词：非负矩阵分解;稀疏表示;重构样本;人脸识别

DOI：10.11907/rjd k.191257

中图分类号：TP301 文献标识码：A 文章编号：1672-7800（2019）012-0073-05

0引言

在数据时代背景下，人脸识别已经在机场、安防、电子身份、旅游、自助服务等领域逐渐取代其它生物特征。现阶段，基于大数据技术的人脸识别方法均受限于样本标记量大、模型参数合理化及模型训练时间过长等问题，使得其在实际应用过程中无法获得应有的效果。

自1999年，非负矩阵分解（Non-negative Matrix Factor-ization，NMF）算法及其求解模型第一次出现在《Nature》中，就作为一种有效的无监督特征提取方法广泛应用于人脸识别。通过NMF中“数据非负”的约束，寻找高维空间下的低维人脸特征。对人脸图像进行特征提取的过程中，将样本图像按一维列向量排列得到高维特征，采用NMF方法进行降维，复杂度有所降低，但NMF分解时无法表达图像的潜在结构信息。陈子健等提出了Gabor变换和二维NMF融合方法，首先对图像进行Gabor变换，提取人脸特征，然后利用二维NMF进行特征降维，其中二维NMF技术保持图像原始矩阵构成高维数据，但NMF方法在学习原始高维数据时容易忽略高维数据的本征几何结构;王晓华等改进了Gabor变换和二维NMF融合的方法，定性分析了二维NMF矩阵分解过程中空间维数对识别效果的影响，过高的维度设置会导致计算复杂度增加，识别率反而有所下降;刘文培等提出利用NMF重构的人脸图像表示人脸局部之间的内在联系，利用重构图像与原始图像之间的误差摒除冗余信息干扰，丰富了训练样本的多样性，并定性探究了迭代次数对收敛结果的影响;孙静静等将多种改进的NMF算法应用于空间目标识别，定性探究了不同维度值下各算法的识别率和时间复杂度，但未能继续探究选择合适的样本数和维度值使得识别效果更好。与上述方法相比，本文提出了一种自适应NMF参数方法，能够自寻最优NMF的迭代次数T和维度值R构造最优训练集，并利用QR分解稀疏表示进行分类，根据分类结果实时调整参数。实验结果表明，在兼顾保留图像结构信息的同时，可以获得较好的识别率，其识别效果优于传统基于原样本识别方法。

1非负矩阵分解（NMF）

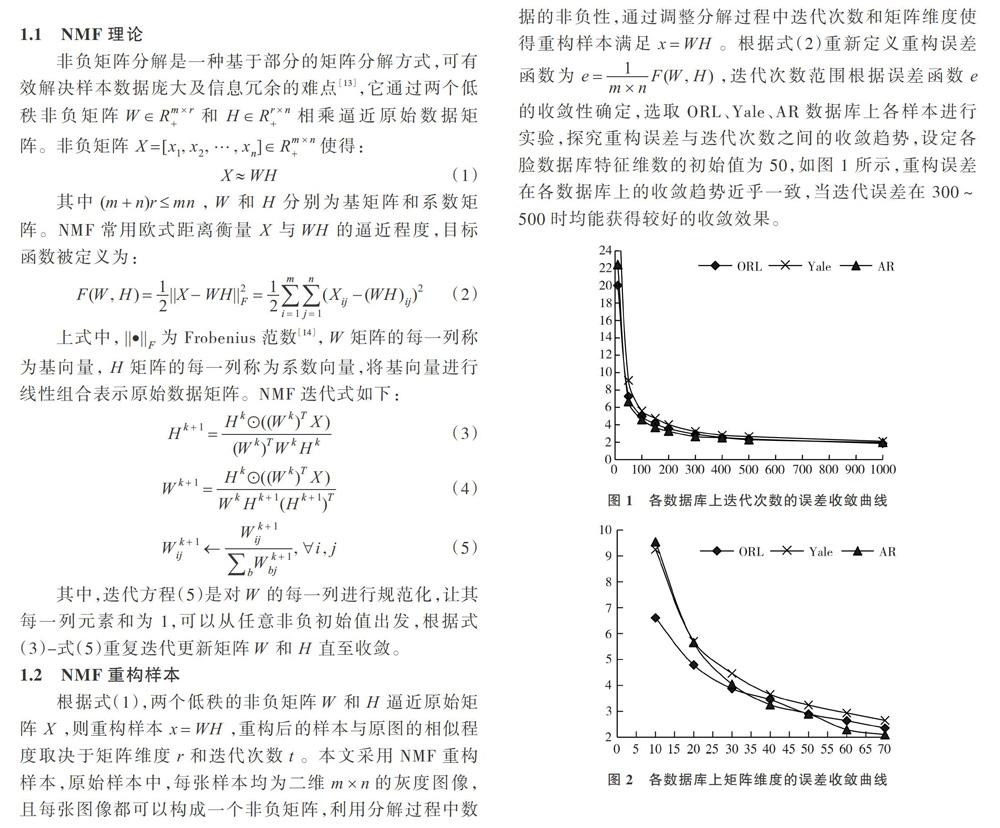
选择适当的迭代次数，既满足误差要求，又不会增加运算次数。设定初始迭代次数为300。根据重构误差e，图2给出了在3个数据库矩阵维度的重构误差收敛曲线，不同的矩阵维度对应的重构误差不同，随着矩阵维度的增大，误差越来越小，当矩阵维度r≤mn（m+n）时，基本可达到较好的收敛效果。

迭代次数t和矩阵维度r不同，得到的样本也不同，随着r和t的增大，重构样本的误差会越来越小，但参数过大会导致计算时间过长，且识别效果已经达到基本稳定，并不会随着参数的增大而无限增大，反而会增加运行时间。本文定量对参数r和t进行自适应分析，选择最优参数丰富样本特征且不增加运算成本。

2QR分解稀疏表示

稀疏表示（sRC）的基本思路是将待测试样本表示为所有训练样本的线性组合，利用e1范数最小化求出稀疏表示系数，最后根据测试样本在每一类训练样本的重建误差作出分类决策。

4实验结果及分析

为了验证本文方法在人脸识别上的有效性，在标准ORL、Yale和AR人脸数据库上进行实验验证。

4.1数据库

ORL人脸数据库包含了400张不同的人脸图像，分别由40名志愿者，每人10张照片组成，所有照片背景均为黑色，每幅样本图像为112×96像素大小，人脸部分存在面部表情、光照强度和面部朝向方面的差异。

Yale人脸数据库由耶鲁大学计算机视觉与控制中心创建，包含了15位志愿者每人11幅图像，总共165幅灰度图像，同一个体包含了不同光照、表情、姿态（睁眼与闭眼）及遮挡（戴眼镜与不戴眼镜）方面的变化。

AR人脸数据库由西班牙巴塞罗拉计算机视觉中心创建，包含了126位志愿者（76男性和60女性）对应的每人26张人脸图像，每类人脸包含了不同光照、表情变化（微笑、愤怒、冷漠、惊讶和悲伤等）、遮挡（墨镜和围巾）;实验中随机选取包含50位男性和50位女性每人26张共2600张人脸图片进行实验。

在实验中，为了保证稀疏表示过程具有足够多的训练样本充分表示测试样本，保证训练字典的样本数量大于样本维数，同时兼顾图像结构细节信息，在算法测试阶段将原始样本向下取样至28×24像素大小。

4.2样本重构

R值和T值不同，NMF重构图像质量会相差较大。以ORL数据库中一个样本进行重构分析，如图3所示，固定维度R不变，迭代次数太低，重构图像会引入条纹干扰，迭代次数太高，重构图像会近似于原图，但会增加运行时间。如图4所示，固定迭代次数T不变，维度太低，对原图的特征继承不够，会引入额外的干扰信息，维度太高，会使计算复杂度变高。对比迭代次数，和矩阵维度R，参数T对图像质量的影响更大，选择合适的参数T和R，才能充分表达原图特征且减少计算复杂度。

为了探究NMF参数R和T对识别率的影响，以每组参数重构NMF图像，随机每类训练样本数量取值为1～5，在ORL數据库下固定矩阵维度R，识别率随迭代次数T的变化如图5所示。在Yale数据库下固定迭代次数T，识别率随矩阵维度R的变化如图6所示。针对不同数量训练样本下，识别率的变化呈现近似相关性，融合合适的参数R和T，能够获得最佳识别率。

4.3实验结果

为了研究本文方法的有效性，在ORL、Yale和AR人脸库上进行识别率的对比实验与分析。以数据库中每类原样本和NMF重构样本进行对比实验，分别随机选择1～5张样本进行训练，对剩下的样本进行测试，均采用QR分解稀疏表示分类，自适应寻找参数R和T，直到找到最佳识别率。实验环境是Intel Core i7-6800CPU 2.4GHz，8GB运行内存和MATLAB 2016a实验平台条件下进行50次随机取样实验且都是在最佳参数R和T下的平均识别率以及对应的最高识别率，实验结果如表1-表3所示，在样本存在光照、姿态、表情、遮挡等干扰情况下，该方法均具有较好效果。

为了研究本文算法运算时间复杂度，在ORL人脸数据库上进行了实验分析。选取每类样本1～5张样本作为训练集，其余样本作为测试集，同时分析了本文算法在已知最优参数下的时间复杂度。实验结果如表4所示，分别对原图和本文算法在测试阶段的识别时间以及本文算法的参数训练时间进行了实验。结果表明，本文算法在识别测试阶段的时间效率与原图识别时间效率近乎一致;实际应用中，在单次单张、背景单一的测试情况下，可以满足实时性要求;但该方法在自适应参数训练过程中，存在参数训练时间过长的问题。

5结语

本文将NMF应用于人脸识别中，提出了一种自适应非负矩阵分解的人脸识别方法，利用原始图像样本构造NMF重构图像，采用QR分解稀疏表示算法进行分类，算法自适应调整NMF参数找到最佳R和T，使得识别效果最佳。实验结果表明，该方法在人脸表情、光照、角度和遮挡情况下均有一定的鲁棒性，尤其在单样本人脸识别下，效果尤为明显。本文方法对NMF算法及改进具有一定的参考意义，但自适应找寻最优参数训练过程中存在一定计算复杂度，有待进一步研究。