管中电流测量消除地磁干扰方法的技术实现

高志贵

（天津市嘉信技术工程公司，天津 300384）

0 引言

随着经济的快速发展，城市电力电气化的不断推进，埋地钢质管道的安全运营面临着严峻考验。在城市地铁和轻轨等轨道交通运输系统中，一般采用直流牵引走行轨回流的方式驱动。一旦回流通路与大地的绝缘存在问题，巨大的直流电流会流入大地，形成随时间变化的动态杂散电流。杂散电流干扰的危害是在管道的杂散电流流出点，管体会受到强烈的腐蚀。电性干扰的存在严重地威胁着城市地下管道等构筑物的安全，若不采取治理措施，干扰致使管道的管体在短时间内腐蚀穿孔发生管道安全事故，因此对杂散电流的检测显得尤为重要[1]。

常用的杂散电流测试技术包括：检查片腐蚀监测、地电位梯度检测、管地电位正向偏移法、管道电位连续动态监测、杂散电流干扰探针测试法、杂散电流测绘仪SCM检测等方法。结合对仪器的便捷性、时效性、结果分析难易等因素，目前主流先进的测试技术是杂散电流测绘仪SCM检测技术。此技术主要应用磁饱和磁力仪探头获取电流产生的磁场数据，采集数据的主要影响因素有铁磁性物质、电磁信号和地磁场干扰。其中，由于地磁场的广域性、持续性、地域分布性、变化性等特殊性质，使研究如何消除地磁场的影响变为重中之重。

1 遗传算法简介

遗传算法是计算数学中用于解决最佳化的搜索算法，是进化算法的一种。进化算法最初是借鉴了进化生物学中的一些现象而发展起来的，这些现象包括遗传、突变、自然选择以及杂交等。遗传算法通常实现方式为一种计算机模拟。对于一个最优化问题，一定数量的候选解（称为个体）的抽象表示（称为染色体）的种群向更好的解进化。进化从完全随机个体的种群开始，之后一代一代发生。在每一代中，整个种群的适应度被评价，从当前种群中随机地选择多个个体（基于它们的适应度），通过自然选择和突变产生新的生命种群，该种群在算法的下一次迭代中成为当前种群。

遗传算法是解决搜索问题的一种通用算法，对于各种通用问题都可以使用。搜索算法的共同特 征为：

（1）首先组成一组候选解；

（2）依据某些适应性条件测算这些候选解的适应度；

（3）根据适应度保留某些候选解，放弃其他候选解；

（4）对保留的候选解进行某些操作，生成新的候选解。

在遗传算法中，上述几个特征以一种特殊的方式组合在一起：遗传算法基于染色体群的并行搜索，带有猜测性质的选择操作、交换操作和突变 操作。

2 磁饱和磁力仪简介

电磁测量方法是埋地管道腐蚀检测行业主流的检测方法。管道中电流的非接触式测量所使用的传感器为磁饱和磁力仪。利用高磁导率的坡莫合金作为灵敏元件，在弱磁场中就能达到磁饱和。灵敏元件的磁芯为闭合磁路，在其两边绕以匝数相同、绕向相反的激励绕组其外绕以信号绕组。对激励绕组给以交变电压，使灵敏元件达到近于饱和，若无外磁场存在，则两边磁芯产生的磁通波形对称而反向，这时信号绕组将没有感应电压输出。当沿元件轴向存在一外磁场，则两边磁芯在正、负半周内饱和程度不一，产生的磁通量不能互相抵消将有感应电压脉冲输出。其幅度与外磁场大小成正比，据此即可测定外磁场的大小[2]。

在理论上，磁饱和磁力仪在测量理想单一的磁场方面有着优秀的能力，但是实际环境中并非只有单一磁场，其他的磁场信号会导致目标磁场的信噪比降低。主要干扰磁场包括铁磁性物质产生的干扰，例如含铁磁性材料的构筑物；现场环境中电磁波的干扰等以及地磁干扰。对于前两种干扰可采取远离构筑物和低通滤波来消除，而地磁场的特殊性质导致去除地磁干扰的方法相对困难。

3 大地磁场

3.1 大地磁场的分布

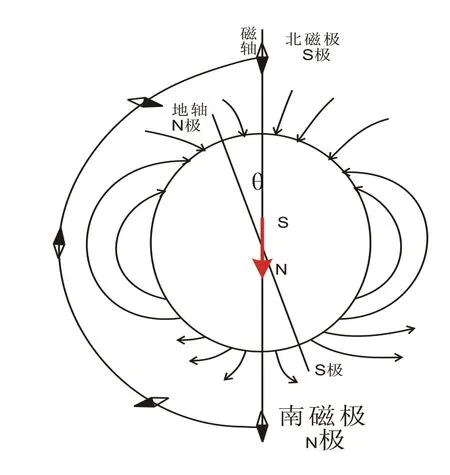
图1 地磁的分布形态

地球磁场近似于放在地心的一个磁偶极子磁场，图1为地磁的分布形态图。地磁场的基本特征 如下：

（1）地球有两个磁极，在地理北极附近的磁极叫北磁极，具有S极性，反之亦然；

（2）磁轴与地球旋转轴不重合，大致相交11.5°；

（3）不同纬度地区，磁力线方向可从磁针的偏转方向判定；

（4）地磁场是矢量场，既有方向也有大小[3]。

3.2 大地磁场要素

图2为地磁的要素，观测点的地磁场矢量（T）为任意方向，它在坐标系内可分解为以下分量：

（1）x分量（北向分量）：在正北方向（X轴）的投影；

（2）y分量（东向分量）：在正东（Y轴）上的投影；

（3）z分量（垂直分量）：在垂直方向（Z轴）上的投影；

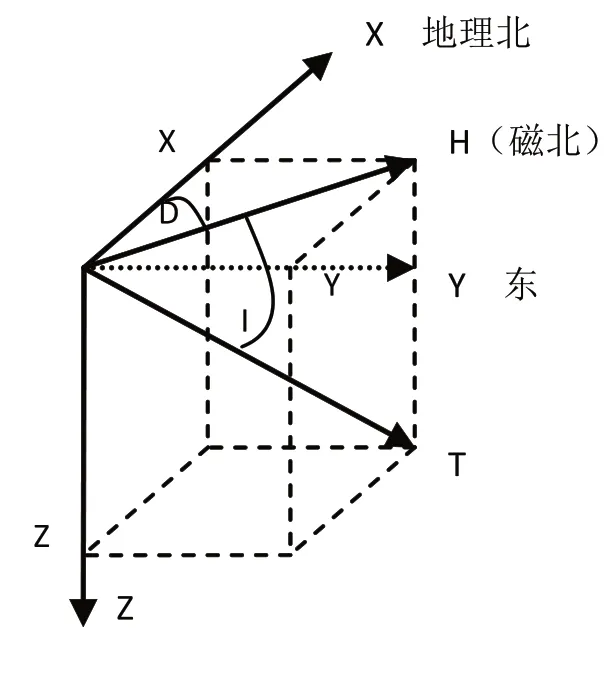
图2 地磁的要素

（4）H分量（水平分量）：在xoy平面上的 投影；

（5）地磁倾角（I）：T与xoy面的交角，约定T下倾为正；

（6）磁偏角（D）：H与地理北的夹角，即磁子午面与地理子午面的夹角，约定磁北自地理北向东偏为正。

4 消除地磁干扰的方法

面对地磁场的种种特性，结合嘉信公司自主研发的杂散电流记录仪（SCL）消除地磁干扰所做研究，提出消除地磁干扰的方法。首先，从仪器的探头方面入手，选用四个性能参数一致的探头，使其探头间误差得到有效控制。

第一次改进是对仪器探头的摆放进行精细的布局控制。图3为仪器探头摆放位置图，将两个用于管道电流I 产生磁场的垂直分量测量的磁饱和磁力仪探头（下称探头），沿与管道轴向垂直方向垂直于地面放置，分别称为3号探头和4号探头，之间的间距为L ，靠近管道一侧的探头即3号探头到经过管道的竖直平面的距离为0.5L。另外以仪器中垂线为轴，探头两两对称布置，实现对地磁的消除。

第二次改进，由于探头内部三轴正交误差以及探头安装时安装平面与三轴的正交存在夹角，使差值计算后地磁干扰没能完全去除，因此对探头引入自适应权值校正系数，进一步对地磁干扰进行去除，已达到更好的效果[4]。

根据毕奥-萨伐尔定律，无限长载流直导体的磁感应强度。

3号和4号探头的磁感应强度为：

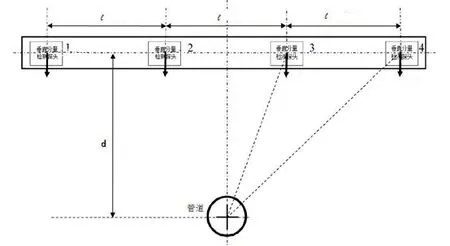
图3 仪器探头摆放位置图

根据电流I相等将②中公式进行合并，将r用l和d来表示，得出管道埋深和电流的计算公式。

（1）测量修正系数β和γ的计算：

安装好仪器后，将1号探头方向分别放置在无电流干扰情况下地磁场的东、南、西、北四个方向上。以磁北为0度，顺时针增大至360度回到磁北。求得在四个方向上B1/B4和B2/B3的比值，即B1标定修正系数β和B2标定修正系数γ。测量结果如表1所示。

表1 四方向修正系数

在标定四方位下B1和B2的修正系数后，便可以通过方位角探头测量仪器实际使用过程中在不同方向角下的B1和B2修正系数；

（2）获得修正值

获得修正系数β和γ后，将此时1号探头和2号探头的测量结果分别进行修正，修正计算公式 如下：

修正后1号位置探头的结果为：

修正后2号位置探头的结果为：

B1和B2是仪器1号探头和2号探头实际测量结果。得到修正后的测量结果后便可以获得更为精确的管道埋深和管中电流。

第三次改进，虽然校正系数能够自动根据方向角对系数进行修正，但此方法过于依赖初始测量获得四方向基础校正系数。由于地磁场的地域分布性和时间变化性，导致换到初始校正地点以外的其他地方时，消除地磁干扰的效果较差；当与初始校正时间不同时，一起测量效果也会发生细小的误差。因此第三次的改进是对自适应权值校正系数加入遗传算法，优化权值，使其更加精确，进一步对地磁干扰进行去除[5]。

由埋深公式变换得出：

因此当埋深d已知时，B3电和B4电就可以通过A来相互变换，将电流I变换成由单独的B3电和B4电来表示。由于地磁干扰没有达到完全的消除，导致3号和4号探头由公式算出的电流值不同，即I差＝｜I3-I4｜≠0。因此反向思考，通过计算单独由3号或4号探头得出的电流值的差值越小，来反映地磁干扰消除越彻底。所以对校正系数β和γ加入遗传算法，使其按照同时增加步长、同时减小步长、一增一减步长四套方案进行迭代，将1号和2号探头的测量结果进行修正，通过I差是否变小即I差next＜I差，来决定迭代方案是否继续。选定方案进入迭代后，当迭代后的I差变大即I差next＞I差时，停止迭代，选定此次计算I差时的校正系数为最终校正系数β和γ，来对1号和2号探头的测量结果进行修正，最终返回测量目标的管中电流值。

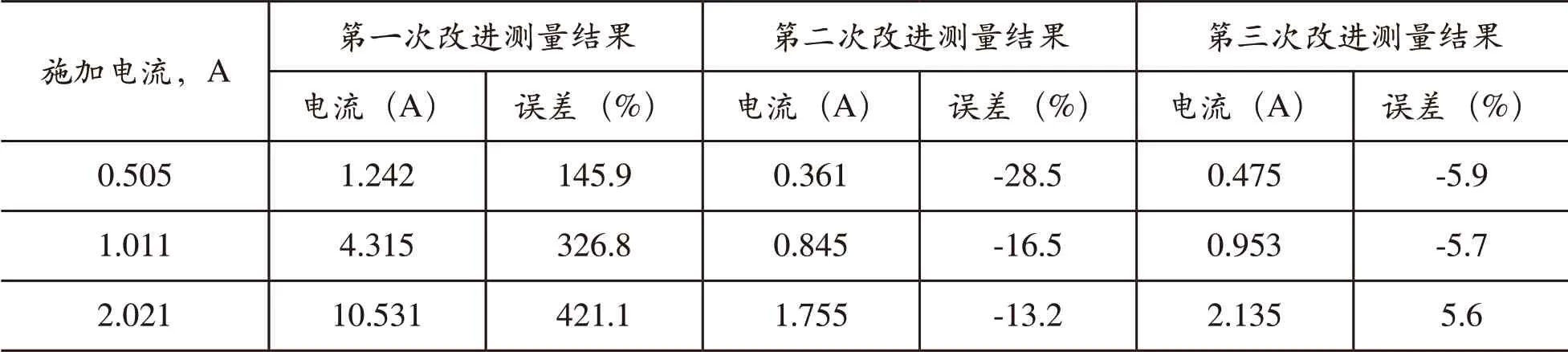
表2 在校正地点进行测量

表3 不在校正地点进行测量

5 改进效果对比

分别对管中施加0.5A，1A，2A的电流，统计三次改进的测量结果。测量结果如表2和表3所示。

结合表2和表3可以看出，在校正地点进行测量时，第二次和第三次改进都有效的消除地磁干扰，效果比较明显，管中电流误差率在30%以内，误差率随电流的增大而减小。但更换测试地点后，第二次改进的测量结果产生较大误差，消除地磁效果明显下降，而加入遗传算法的第三次改进在不同地点都表现出较强的消除地磁干扰的能力，数据结果显示测量误差率最大为8.7%，保持控制在10%以内，相比其他改进效果，误差率最小。表2和表3中第三次改进的数据是迭代30次的结果。验证得知测量误差与迭代次数有关，经过进一步的修正后，测量误差得到大幅度的降低，现已控制在3%以内。

6 结论

加入自适应权值校正系数虽然在校正时的区域消除地磁干扰能力表现优秀，但离开校正时的区域后，消除地磁干扰的能力却大大衰减。对校正系数引入遗传算法后，仪器表现出很强的消除地磁干扰的能力，测量管中电流的误差率在3%以内，误差率随电流的增大而减小。因此加入具备遗传算法的自适应权值校正系数，可以有效消除地磁干扰。