让数学思想之花在初中教学中绽放

施利红

【摘   要】  数学思想犹如天上的繁星，浩瀚无穷，神秘莫测。作为一名初中数学教师，一定要大胆践行数学思想方法，逐步让初中数学思想之花在课堂教学中绽放光芒。

【关键词】  思想;含义;类型;应用;数学

人教版初中数学新教材体系主要包括明暗两条主线，所谓明线就是指基本的数学知识，暗线就是指各种数学思想，它是编写教材的指导思想;明线比较容易理解，暗线不易看懂;明线是围绕“是什么”编写，暗线主要强调“为什么”，学生只有在理解暗线的基础上，才能全方位、深层次理解所学的新知识和新技能。笔者认为，在初中数学课堂教学中，培养学生的数学思想是提高师生互动效率的重要手段。

一、数学思想的含义

数学思想是指人们生活乐园里的空间形式与数学关系反映到脑海里，通过复杂的思维得出言之有理的结论，这既是从本质上理解数学方法和数学内容，又是指导人们探索解决数学问题的原则和观点;既是对数学规律的理性认识，又是对数学基础知识和数学思想方法的升华。但本文阐述的初中数学思想主要指转化思想、数形结合思想、分类讨论思想、函数思想、集合思想等通俗易懂的数学思想，有利于学生深刻理解相应的公式、定义、法则和定理等内容。

二、初中数学思想的比较常见类型及其应用

1.巧用数与数转化思想，轻松找到解决问题的捷径

在初中数学课堂教学中，为了帮助学生攻克一些比较复杂的题目，教师可以通过数与数的转化过程，引导学生找到解决具体问题的途径，这就是数与数的转化思想，它的具体表现包括三个方面：一是把所学的新问题转化为原来已经掌握的问题;二是把比较复杂的问题转化为通俗易懂的问题;三是当新问题用难以理解时，就通过构建新的研究方式解决。

【教学案例1】  现有两个多边形的边数之比是1∶2，它们的内角和度数之比是1∶3，求这两个多边形的边数分别是多少？

笔者在引导学生解题时，先让他们通过仔细阅读后分析，当时大部分学生采取列方程的方法解答此题：先设一个多边形的边数是n，另一个多边形的边数是2n，然后根据题意，并应用多边形内角和公式得出方程：3（n-2）·180°=（2n-2）·180°，最终通过比较繁琐的途径解答了问题。因此，我积极引导学生应用转化思想完成解题：只有从多边形的边数之比与度数之比之间的关系思考入手，才能把度数之比转化为边数之比，从而比较轻松地解决问题。即：从“n 边形的内角和=（n-2）·180°”公式中，当找到求比值之时，就可以约去180°这个公因数。因此，这个问题就变成：“现有两个多边形的边数之比是1∶2，若边数都减少2 时，则其边数之比是1∶3，求这两个多边形的边数分别是多少？”由于灵活应用了转化思想，许多学生在草稿纸上迅速得出结论，一个多边形的边数是：2×2=4，另一个多边形的边数是2×3+2=8或4×2=8。类似的解题方法充分体现了数与数的合理转化思想，为学生提供了比较轻松的解题途径。

2.应用函数与方程思想，以达触类旁通之目的

无论是函数，还是方程，既是重要的数学概念，又是重要的数学思想。所谓函数思想，就是指就应用变化和运动的理念，仔细观察、缜密分析和科学研究具體问题中的数量关系，也就是通过具体函数的形式，巧妙地把数量关系展示出来，从而找到解决问题的具体办法;而方程思想的本质就是把所探究问题的中的相等关系转化为方程式或者方程组等数学模型，最终顺利地解决问题。

【教学案例2】关于x的方程2kx2-2x-3k-2=0的有两个根，其中，一个根大于1，一个根小于1，问：实数k的取值范围是多少？

笔者在帮助学生解答此题时强调：解答这一习题时，假如通过方程的根求解，那计算量就很大，计算过程也比较繁琐，往往出现解题错误的现象。因此，一定要立足于函数方程思想，只有从以下形式转化为一元二次不等式进行求解，才能取得事半功倍的效果：

设y=2kx2-2x-3k-2，根据题意得：k≠0.①当k>0时，二次函数y=2kx2-2x-3k-2与x轴的交点位于点（1，0）的两侧，则当x=1时，y<0即2k-2-3k-2<0，并且这个函数图象的开口方向向上;②当k<0时，二次函数y=2kx2-2x-3k-2与x轴的交点位于点（1，0）的两侧，则当x=1时，y>0即2k-2-3k-2>0，并且它的图象开口方向向下。最后，由①②得出如下结论：k·（2k-2-3k-2）<0.即k2+4k>0，∴k>0或k<-4。

3.强化数形结合思想，培养学生的创新思维能力

在初中数学课堂教学中，教师既可以把数量关系的问题转化为图形的性质进行探究，也可以把图形的问题转化为数量关系的问题解决，这种图形的性质与数量关系有机的方法就是数形结合思想，这与新课标倡导的“运用图形形象地描述问题，利用直观来进行思考”有异曲同工之妙。

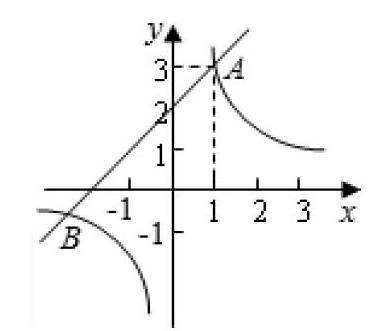
【教学案例3】  如下图所示，已知一次函数y=x+m的图像（m为常数）与反比例函数y=k/x的图像（k≠0）相交于点A（1，3）。

①问：这两个函数的解析式以及图像的另一个交B的坐标。

②结合上述图像计算出函数值y1>y2的自变量的取值范围。

笔者在引导学生解答此题时进行如此分析：为了求出函数解析式，可以采取点转化为数的办法，即：把点A（1，3）代入相应的函数关系式后得出：m=2，k=3;但最终找到两个函数图像的另一交点B的坐标，只有先解答出两个函数联立成的方程组，才能实现数转化为点的目的，即：计算出点B（-3，-1），这样的解题过程就是充分体现数形结合（转化）思想，促使学生理解了抽象的方程组解就是在平面直角坐标系中两个图像交点的坐标。同时，再让学生根据图像写出函数值y1>y2的自变量的取值范围时，可以采取由形转化为数来完成，最终得出函数值y1>y2，即：假如图像处于平面直角坐标系范围内，那么其直线一定处于双曲线的上方位置，最后得出自变量x正确的取值范围：-3

数学思想犹如天上的繁星，浩瀚无穷，神秘莫测。我们一定要与时俱进，开拓创新，继续实践与研究数学思想方法，让初中数学思想之花在课堂教学中绽放光芒。