稀疏分位数投资选择模型及其算法
2019-02-01贺露露张成毅
贺露露 张成毅
[提要] 我们考虑经典Markowitz均值-方差框架内的投资组合选择问题,将其重新定义为一个约束罚稀疏分位数回归问题。我们通过采用Half阈值算法分别将稀疏度k(k的取值分别为6、7、8、9)不同的投资组合随迭代次数收益与误差的变化情况进行分析,从数值实验结果来看,在稀疏度K=7時,能通过较少的迭代次数达到最大的期望值,即可以使投资者的收益最大化。
关键词:稀疏投资选择;Half算法;分位数阈值算法
基金项目:国家自然科学基金项目(编号:11601409);陕西省自然科学基础研究计划青年项目(编号:2017JQ1029)
中图分类号:F83 文献标识码:A
收录日期:2018年10月29日
引言
现代金融学中大规模稀疏投资优化选择问题是十分核心和活跃的研究课题之一,如何最优的去选择金融产品的投资组合以达到收益最大、风险最小的均衡状态,是各级金融机构乃至个人投资者关注的核心问题。
1952年,哈里·马科维茨就这个问题在The Journal of Finance期刊上发表了一篇名为“Portfolio Selection”的文章,提出了均值-方差(MV)投资组合模型,从而开创了在投资收益和风险不确定的情况下理性投资者进行资产组合的理论和方法,为现代金融学的发展奠定了基础。但是,M-V投资组合模型却存在一些不足之处。首先,由于人们对大规模的资产组合的期望收益率向量与协方差矩阵的估计比较困难,从而导致在实证分析中存在着较大的估计误差,所以M-V模型的计算复杂性大;其次,模型中资产期望收益和方差-协方差矩阵的估计完全依赖有限的样本数据,容易引起估计有很大的偏差且时间的可变性,尤其对期望收益有强烈的时间可变性;最后,均值-方差投资组合模型是以资产收益的有限样本估计(和)的估计误差被不合理地放大的形式构建的。因此,所得投资组合具有误差最大特征,并且对于个体资产的期望收益的意外小扰动是极其敏感的。总之,Markowitz投资组合模型极大地受到估计误差的影响,具有比较差的样本外性质,从而经常导致非常不稳定且极端的资产组合权重。
其后,为解决投资组合选择理论在实际应用过程中的困难,Sharp在文章中改进了并发展了Markowitz模型,与Litner and Mossin建立了资本资产定价理论 (CAPM),使繁杂的计算工作得到了简化。由于Markowitz与Sharpe在金融学领域所做出的开创性的贡献,使得他们与Merton在1990年度共同获得了诺贝尔经济学奖。
除此之外,而我们正处于大数据时代,身处于这个时代,证券市场的各式各样的股票或许就会让投资者迷茫不已,更有各式各样的金融衍生产品令人眼花缭乱,目不暇接。从庞大的数据之中进行投资组合的选择是金融机构、企业、投资者一直需要解决的问题。
以往人们通常选择基于最小二乘法来建立投资选择模型。这类模型的目标函数是凸的光滑函数,容易处理,并且有现成的算法。然而,这类模型也有其致命的弱点,最主要的是所得结果极其不稳定,并且在实际的经济生活中会出现尖峰或厚尾的分布、存在显著的异方差等情况,此时最小二乘估计的稳健性非常差,不具有样本外性质。而分位数回归模型相比于最小二乘投资选择模型而言,能够精确的描述解释变量对于被解释变量的变化范围的影响能够更加全面的描述被解释变量分布的全貌,而不仅仅是分析被解释变量的条件分布的期望(均值)位置;可以分析解释变量如何影响被解释变量的分位数等。尤其在金融投资组合模型中,可以通过取不同的分位数值来解决不同的问题,使得模型具有稳定性。
于是,1978年Koenker and Basset提出了分位数回归的理论和方法,这是一种代替一般最小二乘回归的重要方法,通过分位数0~1之间的任何值,调节回归平面的位置和转向,让自变量估计不同分位数的因变量,对随机误差的分布不做任何要求,当分布不对称、厚尾或者删失时,这种分析法尤其有效,因此与经典的最小二乘法相比在应用上具有独特的优势。
一、稀疏分位数投资选择模型的提出
稀疏投资组合模型就是基于Markowitz模型的结构将其目标函数增加一个以投资组合权重为变量的罚函数来构建的。通过罚正则化优化问题,可以使得投资组合变得具有稀疏性。如下就是稀疏分位数投资选择模型:
设定Rn×m=(r1,r2,…,rm)是包含解释变量的设计矩阵,我们要研究的线性模型是:


三、数值实验结果与分析
本文通过构建L1罚分位数稀疏投资选择模型,实验过程就是将分位数回归下的Half阈值算法同Lasso算法分别应用到分位数模型上,各自得到实验结果。首先本文的数据实验来源于1992~1997年的一系列市场标准恒生指数,其中每列的数据是所有资产股票在不同时期的历史收益数据。本文的编程环境是SAMSUNG Q470C pc (Intel Core i3-3110MCPU,2.40GHZ,4.00GB)上matlab-R2015b中完成。
图1~图4将展示Half算法当改变稀疏度时,期望值随迭代次数的变化。从图中可以看出,当随着迭代次数增加时,期望值将穩定在一个固定值,即:投资者收益很稳定。(图1~图4)
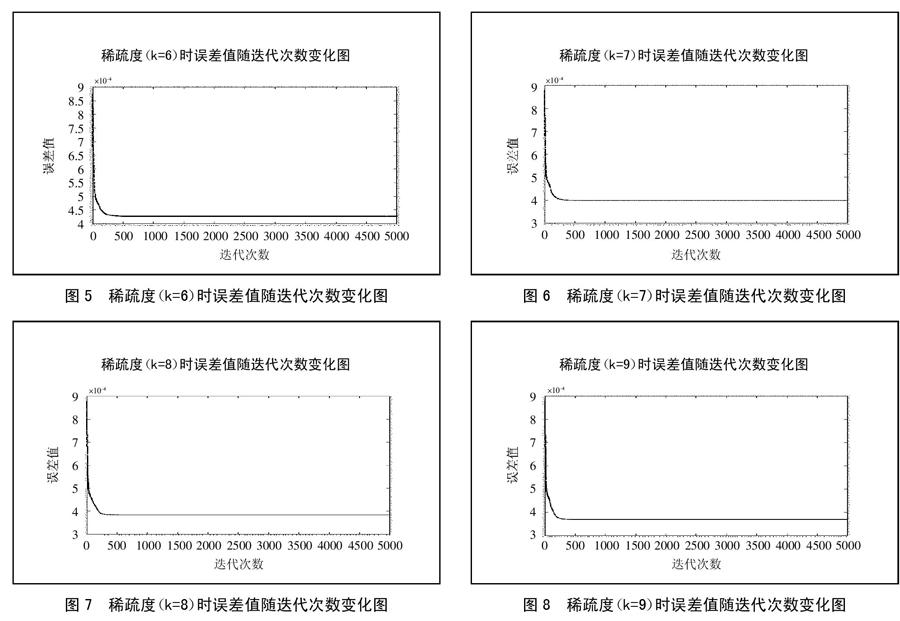
从图5~图8来看,随着迭代次数增加时,误差将越来越少,并且不同的稀疏条件下,误差影响差别较小。(图5~图8)
四、小结
本文将分位数回归下的Half阈值算法应用到投资选择模型上,从实验结果来看,当随着迭代步数,期望将越稳定。并且在稀疏度K=7时,能通过较少的迭代次数达到最大的期望值,即可以使得投资者收益最大化。
主要参考文献:
[1]Markowitz,H.M.Mean-variance analysis in portfolio choice and capital markets.J.Finance,1952.77-91.
[2]SHARPE W.F.A simple model for portfolio analysis[J].Management Science,1963.9.
[3]SHARPE W.F.Capital asset prices:a theory of market equilibrium under conditions of risk[J].The Journal of Finance,1964.19.
[4]JOHNS L. The valuation of risk assets and the selection of risk investments in stock portfolios and capital budgets[J].Review of Economics and Statistics,1965.47.
[5]MOSSIN J.Optimal multi-period portfolio policies[J].Journal of Business,1968.41.
[6]KOENKER R,BASSETT G.Regression quantiles[J].Econometrica,1978.46(1).
[7]NASSIRI V,LORIS I.An efficient algorithm for structured sparse quantile regression [J].2014.29(5).
