HPM视角下反证法的教学设计研究
2019-01-30张艳蓉张府柱
张艳蓉 张府柱

摘 要:该文从数学史融入数学教学的视角,开发教学设计,在真实的教学情境中实践教学设计。研究梳理了数学教育领域的相关理论,从学生认知、思想方法和数学史3个维度来设计课堂教学,并总结出数学史融入数学教学的一般流程。
关键词:HPM 反证法 教学设计
中图分类号:G642 文献标识码:A 文章编号:1672-3791(2019)11(b)-0120-03
近几年,关于HPM的研究发展迅速,HPM的文章也是层出不穷,但文章的涉及面很多是中小学。基于已有的研究出发,能够以HPM的视角对反证法进行教学,采用设计研究的方法,解决反证法教与学的问题,并以此更深一步研究,主要围绕以下问题展开。
(1)学生理解反证法是否呈现出历史相似性,历史相似性研究是HPM领域研究中的一个方向,也是HPM研究者进行数学史融入数学教学的理论基础。
(2)HPM视角下反证法教学对学生对数学概念、定义的理解以及对学生的情感态度与价值观有什么影响?从HPM视角下去实施教学,问题是此教学是否对学生有影响,能否解决教学中存在的问题。
(3)HPM视角下数学反证法教学对教师的专业发展有什么影响?可以从教师对HPM教学知识、教学能力、教学信念来考察参与HPM视角下数学反证法教学过程中的专业发展,此问题可以分解为:①HPM视角下数学反证法教学对教师的信念产生的影响;②HPM视角下数学反证法教学对教师知识产生的影响;③HPM视角下数学反证法对教师的教学能力产生的影响。
1 数学反证法的历史
数学的发展出现过3次危机,每一次都和一个悖论有关,而最终的解决又势必推动数学的向前发展,取得重大的突破,产生划时代的数学成就。
什么是悖论呢?从推理过程看上去合乎情理,但结果却得出了矛盾。悖论在很多情况下表现得出不符合排中律的矛盾命题:由真,可以推出它为假;由假,则可以推出它为真。这种严格性大家公认为是数学的一个主要特点,因此如果数学中出现悖论则会造成对数学可靠性的怀疑。
第一次数学危机由希帕索斯悖论引发,这个悖论的产生和勾股定理有着密切的联系,并且最终促成了无理数的发现,对以后的数学发展产生了深远的影响,在解决这次危机的过程中,有许许多多的科学家为之付出了努力,有的甚至还付出了生命的代价。
数学第一次危机发生在公元前580~568年之间的古希腊,数学家、哲学家毕达哥拉斯创立了毕达哥拉斯学派,这个学派发现并且证明了勾股定理,毕达哥拉斯在完成这一定理证明后欣喜若狂,杀牛百只以示庆贺。因此,这一定理还又获得了一个带神秘色彩的称号:“百牛定理”,所以在西方将勾股定理称为毕达哥拉斯定理[3]。
“万物皆数”是该学派的哲学基石,是毕达哥拉斯提出的著名命题“一切数均可表示成整数或整数之比”,因为整数可以看成是分母为1的分数,整数与整数的比就是分数,分数和有理数的等价性,整数或整数之比实际上就是有理数,毕达哥拉斯学派的数学信仰就是现在我们所熟悉“一切数都可以表示成分数”。毕达哥拉斯定理(勾股定理)提出后,希帕索斯(学派中的一个成员)发现了一个问题:一个边长为1的正方形的对角线长度既不能用整数表示,也不能用分数表示,而只能用另外一个属来表示,这个数就是,这就是希帕索斯悖论,也叫作毕达哥拉斯悖论。这个的出现在数学界掀起了一场风暴。它直接动摇了毕达哥拉斯学派的数学信仰,使毕达哥拉斯学派为之大为恐慌。
在当时直接导致了人们认识上的危机,毕达哥拉斯学派认为希帕索斯就是魔鬼的化身,这位天才的思想家被投进了大海,为科学献身的第一人。但是希帕索斯的名字却和一样,让后人永远地记住了他,希帕索斯也成了有史以来第一个使用反证法的人。
设正方形的边长为1,其对角线为a,那么根据毕达哥拉斯定理α2=2,假设a是分数,设(p,q既约),有,即,从而可得q是一个偶数,那么q也是一个偶数,再令q=2m,代到q2=2p2里面,4m2=2p2也就是4m2=p2,这样就得到p2是一个偶数,那么p也一定是一个偶数,这和p,q既约是相矛盾的,从而可以得到a不能表示成分数,也就是说边长为1的正方形的对角线不能用整数之比来表示。
这种现象并不是唯一的,而是普遍的,比方一边长为1另一边长为2的矩形的对角线也不能用整数之比来表示,这无异于在平静的水面上投下了一块巨石一般,在当时的数学上和认识上掀起了轩然大波,引起了认识上的恐慌。为了摆脱这种尴尬,许多学者开始致力于化解这一危机。从这次数学危机得出,仅凭直觉和经验不一定正确,要经过推理证明才是可靠的。
2 反證法教学设计与研究
反证法是逆向思维的典型方法,其独特的思维方式对提高数学思想有着重要的意义。它不仅具有强大的论证威力,而且越是困难的问题它越有功效。要想深刻理解反证法,就要深刻地领悟“正难则反”的思维原理。通过证明反论题为假而间接证明原论题为真的方法,叫作反证法,反证法证明步骤。
(1)反设:假设命题的结论不成立,即假设结论的反面成立,这个假设叫作“反证假设”。
(2)归谬:由反证假设出发,运用已知条件,进行正确推理,导致矛盾。
(3)肯定:由所得矛盾,断定反证假设不成立,从而肯定结论成立。
其中第(2)步是关键,主要寻找以下矛盾:与反证假设相矛盾;与已知条件相矛盾;与已知事实、定义、公理、前此定理相矛盾;自相矛盾。
3 反证法应用
当用直接证法无法下手甚至不可能时,可使用反证法。
反证法更适用于:否定性问题;唯一性问题;存在性问题;无限性问题;同一性问题(逆命题成立);学科起始性定理;命题结论的反面中唯一,应用穷举反证法。基于HPM反证法的教学设计需要考虑教学设计要解决教学问题,需要了解具体的数学内容的历史,科学准确地理解其本质,在学生现有的认知基础上,应用教学理论来完成教学设计。在教学设计中恰当地融入数学史,使得教学更加符合学生认知,学生更容易理解,更好地解决数学问题,提高学生学习兴趣,增强学生学习自信心[1]。
3.1 教学设计的3个维度
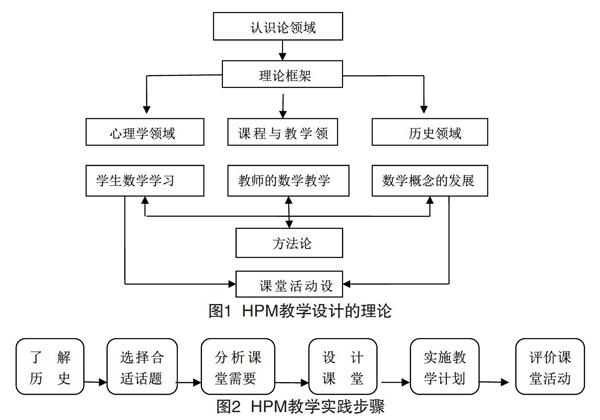
一个教学设计要考虑课程与教学论领域,同时还要注意课程标准、教学内容、教学方法,教师的数学教学观等直接影响到教学(见图1)。
如何设计HPM理论与实践连接,把数学史融入到教学中,从而设计有效的教案;关键是促进教师专业发展,引领教师的HPM。通过建立HPM学术共同体把HPM领域教学实践,从理论与实践两个方面解決上述问题(见图2)。
3.2 教学设计的策略
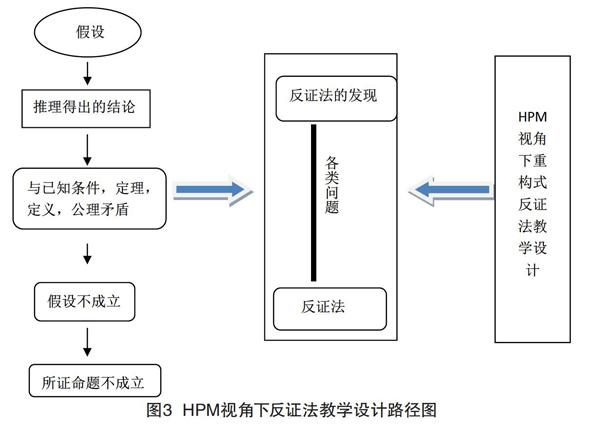
融入数学史的反证法教学,关键部分就是教学设计,如何设计HPM视角下的反证法教案呢,经过阅读部分研究者的HPM的设计及反证法的教学有了设计思路(见图3)。
根据以上HPM设计框架初步设计了反证法的教学设计,让学生经历数学反证法的演进过程,从中发现反证法的原理,以重构式来进行反证法概念教学,以系列趣味题来激起学习的兴趣,在探索中学习历史,发现数学。
4 反证法研究的学生反馈及教学反思
(1)这种融入教学史的方式受到学生的喜欢,学生情感价值观也得到提升,培养了学生探索创新的能力,但是学生的成绩或理解水平没有得到很大的提升,这也反映出1、2次的课程的HPM教学不可能改变学生的成绩,只有通过长期的HPM教学实践,才能改变学生的学习兴趣,培养学生的学习模式。从对学生的反馈来看,仍有不少学生表示反证法不好理解,效果也没有想象得好,实践中还需继续摸索。
(2)HPM视角下的反证法教学,仅仅教学研究的需要和尝试,教师准备也比较费时,但也有利于教师的专业发展。首先,教师的教育信念有了变化,教师认识到让学生理解定义及定理的重要,数学历史让教师感受到对学生认知的理解的重要性。其次,教师教学知识的增加了不少,在教学设计过程中,教师的数学史知识有所增加;教师了解教学设计的大体思路,如何设计更有利于达到教学效果。最后,教师的教学能力也得到提升,表现在教师开始有意识地关注与学生的互动,利用机会去激发学习动机,引导学生讨论;同时,意识到在设计教学时,需关注学生的认知起点及认知过程的渐进性,知道选择加工史料的方式方法,了解到如何从教育研究的角度帮助教学。
5 研究的启示
反证法教学设计要考虑学生的认识情况、对反证法的理解、对数学史的认识,建立数学的学习要与数学的历史发展相联系,有效地设计把数学史融入到课堂教学中去。通过研究述,构建了数学史融入数学课堂教学模式,总结出数学史融入数学课堂教学的一般实施流程。数学史融入数学课堂教学对老师要求更高,把数学史融入课堂教学需要老师将数学史的资料进行加工,使学生容易吸收真正达到优化课堂教学如何培养领域的教师专业化,如何促进教师应用来提升教学率。当前教师面临着数学史知识缺乏、学生的升学压力以及可直接应用的HPM视角下数学归纳法教学的设计研究案例缺乏等问题。解决这些问题的根本方法就是探索出领域的教师专业发展模式,以及详细地分析教师专业发展的分析框架。
参考文献
[1] 冯振举,曲安京.HPM视野下的数学新课程内容构成[J].课程教材教法,2007,27(9):38-42.
[2] 尹静,王笃勤.教育设计研究与教师实践性知识的构建[J].河北大学学报:哲学社会科学版,2013,38(2):65-68.
[3] 李文林.数学史概论[M].3版.北京:高等教育出版社,2011.
[4] 周余峰.一次公开课的启示——谈新课程理念下的教学观[J].数学教学通讯:中等教育,2013(24):27-28.
[5] 陈惠勇.数学史观下的数学概念教学新模式[J].高等数学研究,2007,10(5):58-62.
[6] 沈卫国.康托对角线法中的逻辑问题及由此引出的反证法使用中必须注意的推理误区[J].前沿科学,2017,11(2):42-50.
