考虑经济性的可再生能源并网研究

， ， ，

(1.国网上海市电力公司松江供电公司,上海 201600；2.上海电机学院 电气学院，上海 201306；3.上海电机学院 汽车学院，上海 201306)

0 引 言

随着环保要求的不断提升，可再生能源建设规模不断扩大。在可再生能源占比不断提高的同时，可再生能源发电并网过程中也带来了难以控制、受环境影响大和继电保护整定难等一系列问题[1-3]。目前国内外学者的研究也主要集中在以上几个方面，并取得了一定的研究成果[4-7]。这些对更好地利用可再生能源提供了保障，特别是在能源互联网背景下，能够最大限度地消纳可再生能源。

在关注可再生能源的利用与消纳的同时还需要关注另外一个问题，就是可再生能源并网后电网运行的经济性。达到全社会效益最大化是利用可再生能源的最终目标，而电网的经济运行是其中很重要的一个方面，以往在这方面研究较少，本文在这方面作了有益的试探性的研究。

在电力网络方程当中，支路量和电流量在配网的分析中有一些应用之外[8-10]，还是很少被作为状态变量的。文献[11-13]在电气元件的π型等值电路基础上，将节点注入功率等值为电压源，而以阻抗支路为链支，接地支路为树支，建立电力网络分析的支路电流-节点电压混合方程，实现了电力网络的支路状态变量表示方式。在上述研究中，作为电力网络中最明显的特征，潮流量被直接体现出来，在直角坐标系下混合表示的电力网络方程针对节点电压是二次的，而针对支路电流是线性的，通过以支路电流作为状态变量对电力系统进行分析，相当于变换了分析问题的角度，从另一个侧面发现了一些值得深入研究的问题。

1 增加支路电流变量的电力网络方程

1.1 电网设备的π型等值电路

电力网络是由线路、变压器等输电设备组成的，在集中参数电力网络中，通常以π型等值电路来对输电设备进行模拟，即一个输电设备可以表示为三条支路，包括一条阻抗支路和两条对地支路，如图1所示。假设系统中有N个节点L条支路。其中:支路阻抗矩阵为Z=R+jX，为L×L阶矩阵，R为支路电阻，X为支路电抗；对地支路导纳矩阵为Yg=Gg+jBg，为N×N阶矩阵，Gg为对地支路电导，Bg为对地支路电纳；I=Ia+jIr表示阻抗支路电流向量，为L×N阶矩阵，Ia为电流向量实部，Ir为电流向量虚部。

对地支路一端接地，而另一端并联在节点上，在接地的一端注入为0，可以以等效电流源来表示，如图1所示，其中IL表示节点注入电流源。对于每一条接地支路来说，电流的走向经过两条途径，即对地的电容支路电流IG和负荷支路电流IL，但是在负荷支路电流IL中流过的不仅是该回路的电流，还有相邻回路的电流。因此，电力网络方程包括两部分，即阻抗支路方程和对地支路方程。

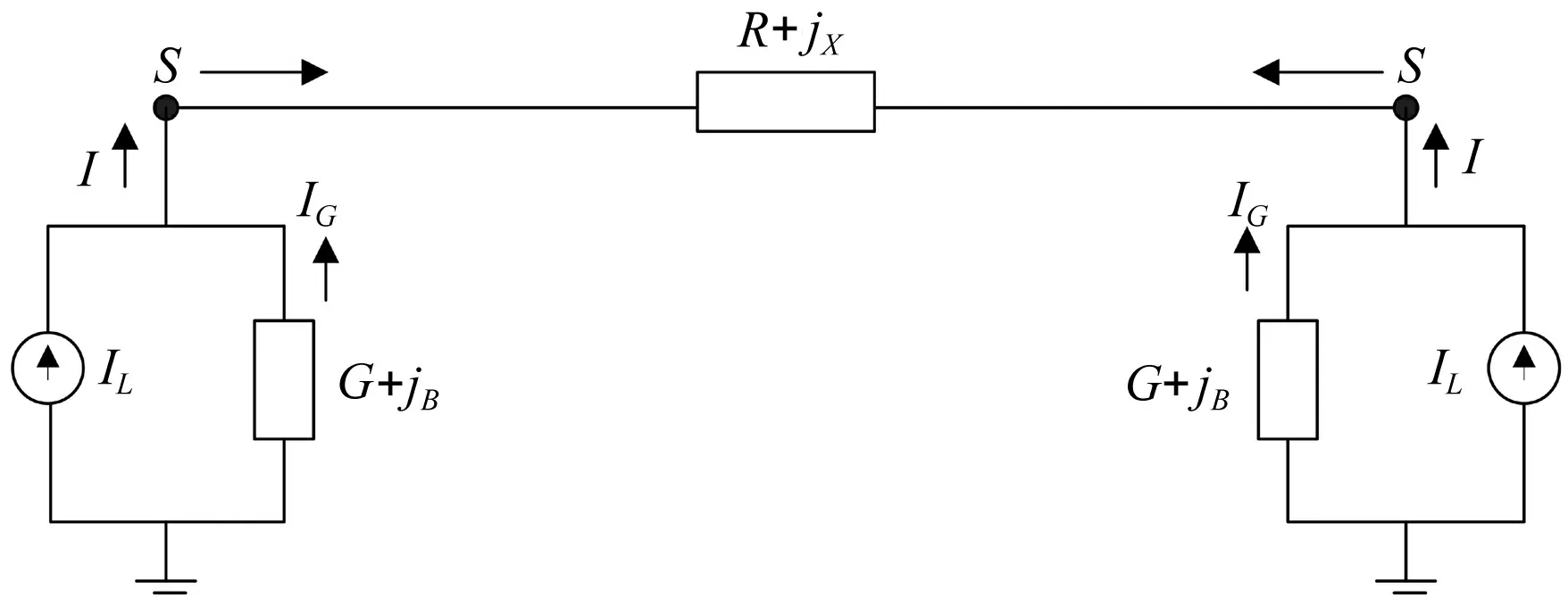
图1 等效电流源π型等值电路图

1.2 阻抗支路方程

设节点电压向量矩阵为：U=Vcosθ+jVsinθ，为N×N阶矩阵，V为电压幅值，θ为相角，阻抗支路方程可以描述为：

ZI=ATU

(1)

式中:A表示支路-节点关联矩阵，为N×L阶矩阵。两边乘以矩阵A，并令Yc=Z-1，得：

AI=AYcATU

(2)

令Ys=AYcAT=Gs+jBs，其与节点导纳矩阵的区别在于不含有接地支路的导纳值。将式(2)展开，得：

AIa=(Gscosθ-Bssinθ)V
AIr=(Gssinθ+Bscosθ)V

(3)

式(3)即是节点电压与支路电流关系方程，可以看出，节点电压和支路电流之间为线性关系，如果已知节点电压则很容易求得支路电流。

1.3 对地支路方程

(4)

由

(5)

将式(4)、式(5)展开，并且为了简化计算忽略对地支路电导，得：

Q=sinθVAIa-cosθVAIr-VBgV

(6)

P=VcosθAIa+sinθVAIr

(7)

由此可见，通过支路电流变量的引入，电力网络方程可以由式(3)和式(6)、式(7)构成的方程组来描述，方程组的主要特点是：网络方程相对于支路电流变量是线性的，相对于节点电压变量是非线性的。相较于传统节点电压表示的电力网络方程，由于支路电流变量的引入使得对电力网络运行状态的观测性增强了。

2 基于支路电流变量的网损最小优化模型

2.1 网损最小优化模型

电网经济性优化模型采用全局网损最小的优化目标函数，可表示为：

(8)

式中:l=1,2,…,L。等式约束即为式(3)、式(6)、式(7)，不等式约束如下：

(9)

式中:节点i电压Vi可由式(7)求得;节点i无功功率Qi由公式(6)解得。

2.2 模型求解

(10)

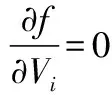
该优化模型求解的迭代步骤如下：

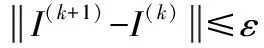
3 算例分析

本文选取的案例分析目标电网为上海某园区10 kV配电网络。园区供电线路均为电缆，线路供电半径较短，所带负荷较大，采用环网供电模式，开环运行。变电站到开关站电缆型号均为400 mm2，开关站以下为240 mm2。系统共40节点，42条支路，部分接线如图2所示。该配电系统典型日最大负荷在21 MW左右。

(1)假设在尼乐园西关站接入可再生能源，通过上述优化算法计算接入的可再生能源容量，同时与接入其他容量可再生能源产生的网损进行分析比较。从表1中尼乐园西开关站计算结果可以看出，在尼乐园西开关站母线接入可再生能源容量为3.96 MW时网损为0.634 MW，达到最小。系统网损变化趋势是随着可再生能源的容量增加，呈现先下降后上升的凹形抛物线。

(2)在尼乐园北开关站接入不同容量的可再生能源，分析可再生能源对网损的影响。

由表1中尼乐园北开关站计算结果可知：在不同节点安装可再生能源都可以达到降低网损的目的，但不同节点达到的最小值不尽相同，从上面计算结果可以看出尼乐园北开关站网络损耗下降的幅度是比较大的，这是因为尼乐园北开关站所带负荷较重，接入可再生能源的降损效果最好。因此，在当前环境保护的背景下，多种可再生能源可供选择接入电网，电力企业在制订运行方式时可以按照网损最小的方式安排可再生能源的出力，达到电网经济运行的目的。

表1 尼乐园开关站接入可再生能源的网损计算结果

图2 园区网络接线图

4 结束语

通过建立的网络损耗计算优化模型以及仿真计算结果可以得到如下结论：

(1)本文提出的引入支路电流作为计算变量的电力网络经济性优化方法是可行的，提出了解决网损优化等问题的新途径。

(2)在对可再生能源接入电网容量的计算过程中可以得到网络损耗最小的可再生能源接入容量，为电力部门运行方式安排提供了依据。

(3)进一步分析可知，可再生能源在配电网节点接入可以起到降低网损的作用，但网损并不呈线性下降，随着可再生能源容量的增加网损会达到一个最小值，之后网损会增大，呈凹形抛物线的形状。