高中“导师制+互助学习小组活动”管理模式下智慧的上好《水平面内的匀速圆周运动》的策略

广东省韶关市仁化县仁化中学 刘丽娜 陈 君

一、对教材整体分析

（一）对知识点分析

本节内容是粤教版高中物理必修2第二章《匀速圆周运动》的第4节内容，在此之前，学生已经初步认识了匀速圆周运动，会用线速度、角速度、周期、频率描述匀速圆周运动的快慢。通过第二节向心力和向心加速度内容的学习，学生已经知道了向心力的大小与质量、角速度、半径的定量关系。第三节通过匀速圆周运动基本规律，结合实际生活中的两个实例“火车转弯”和“汽车过拱桥”进行分析，学生已经明确了向心力的来源，知道向心力是按效果命名的力，任何一个力或几个力的合力都可以提供向心力。那么本节课立足于匀速圆周运动基本规律上，结合几种常见的水平面内匀速圆周运动的典型模型及其临界条件进行分析，旨在对向心力来源的知识巩固和对临界问题的分析。所谓临界问题，一般是指物体的运动形式，或者物理现象、物理过程转变的过程中，存在着分界的问题。物体处于这种转变状态，称为临界状态，此时物体既具有转变前的基本特点，又具有转变后的基本特点。而要实现这种转变是有条件的，称为临界条件，常涉及一个或几个物理量达到特殊值(临界值)，而临界值大多以极值的形式表现出来，如最大值、最小值和零值。

（二）对重难点分析

对于现在的高中生来说，很多学生做理科题目时总是出现眼高手低的习惯，一道题会说但不会写，缺乏动手规范答题的能力，为了让学生养成良好的答题规范，本节课的重点之一是要明确物体在水平面内做匀速圆周运动的解题步骤。其次，对于临界问题是高考的重点也是难点，在2014年全国I卷中第20题就出现了关于此临界问题，所以本节课的重点之二是水平面内匀速圆周运动的临界问题。如何运用所学知识解决水平面内匀速圆周运动的临界问题是本节课的难点。

（三）对教育目标分析

在解决水平面内的匀速圆周运动时，分析其受力情况以及运用牛顿运动定律解决问题很重要，这是做此类题目的关键，并且还要掌握解决圆周运动的一般方法和特殊方法，提高综合分析问题的能力。分析临界问题时，首先要找出临界状态和临界条件，学会把复杂问题分成很多小的问题，然后逐个突破，在学习的过程中通过小组互助合作探究，能够培养学生科学的认知态度，提升合作意识和探究精神，并且能够在小组互助活动中感受学习物理成功的乐趣与体验在科技生活实际中运用的价值。

（四）对教育策略分析

本节课主要采用“问题导入式+小组互助合作”的教学策略，符合学生为主体,教师为主导的原则。首先通过问题导入，学生自主思考，老师引导，让学生明确物体在水平面内做匀速圆周运动的典型模型有哪些？临界状态怎样？其次通过学生讨论，小组互助合作，小组展示，让学生进一步熟练圆周运动问题的解题步骤；第三通过学生讨论，小组互助合作，教师点评，达到知道圆周运动中临界问题，并能正确解题的目标。

二、采用符合学情的教学模式

（一）传统高中物理教学模式与当今比较先进的物理教学模式的对比

传统高中物理教学模式可概括表述为“复习导入--传授新知--总结归纳--巩固练习--布置作业”，它是我国长期以来物理教学的主流模式。当今比较先进的物理教学模式可概括表述为“创设情境，提出问题--讨论问题，提出方案--交流方案，解决问题--模拟练习，运用问题--归纳总结，完善认识”。这种教学模式脱胎于传统物理教学模式，力求重视教师的主导作用和学生的主体作用。“创设情境，提出问题”，没有考虑学生在物理学习中生成或遇到的新问题；“讨论问题，提出方案”，没有给学生独立自主解决问题的时空；“交流方案，解决问题”，没有考虑学生多角度思考解决问题的途径和方法，只是建立单一的物理模型；“模拟练习，运用问题”，没有考虑运用物理模型去解决新的物理问题；“归纳总结，完善认识”，强调的是单一的物理模型认识。

（二）符合学情的“问题导入式+小组互助合作”教学模式

我们提出“问题导入式+小组互助合作”这种高中物理教学模式，是因为问题是思维的土壤，问题是教学的心脏，问题的有效产生和发现往往认为是高质量教学的逻辑生长点[1]。并且旨在为学生自主学习提供一个优良环境，将学生置于广阔的社会时空中去体验物理、理解物理、认识物理、学习物理、运用物理，最大限度地发挥学生学习物理的自主性、主动性和创造性。培养学生的物理问题意识和物理问题能力、物理探索意识和物理探索能力、物理交流意识和物理交流能力。

小组互助合作学习是在班级授课制背景上的一种教学方式，即在承认课堂教学为基本教学组织形式的前提下，教师以学生“小组互助合作”为重要的推动性，通过指导小组成员展开合作，发挥群体的积极功能，提高个体的学习动力和能力，达到完成特定的教学任务的目的。下面以具体的教学实践案例来进行探讨。

任何理论都必须用实践来检验，本文以高中物理粤教版必修二第二章里面的主题为“水平面内的匀速圆周运动”为例进行分析。

三、认真落实模式的各个环节

（一）问题导入，学生自主思考，老师引导

首先，请同学们思考以下几个问题？

问题1：一般的受力分析顺序？（学生答：一般顺序为重力、弹力、摩擦力、已知外力等）

问题2：物体做匀速圆周运动的条件？（学生答：合外力提供向心力）

下面同学们再思考一个问题：物体在水平面内做匀速圆周运动的典型基本模型有哪些？

学生答：一根绳拉一个小球在水平面内做圆锥摆运动、一个小物块在圆筒侧壁上与圆筒相对静止做匀速圆周运动、一个小物块在水平放置的圆盘上随圆盘一起相对静止在水平面内做匀速圆周运动等等。

根据学生的回答，老师作了以下总结：

水平面内匀速圆周运动的典型模型可以概括为以下三种：

（1）与绳子弹力有关的匀速圆周运动（2）与支持面弹力有关的匀速圆周运动（3）与静摩擦力有关的匀速圆周运动。

（二）学生讨论，小组互助合作，小组展示成果

通过前面的自主思考，我们总结了三种典型的水平面内的匀速圆周运动的模型，下面请同学们按学习小组进行问题的探讨：

1.与绳子弹力有关的匀速圆周运动

问题1.如图1所示，小球做圆锥摆时细绳长为L，与竖直方向成θ角，求小球做匀速圆周运动的角速度ω。

2.与支持面弹力有关的匀速圆周运动

问题2：如图2所示，半径为r的圆筒绕竖直中心轴转动，小橡皮块紧贴在圆筒内壁上，它与圆筒的摩擦因数为μ，现要使小橡皮不落下，则圆筒的角速度至少多大？

（最大静摩擦力等于滑动摩擦力）

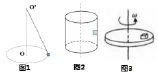
3.与静摩擦力有关的匀速圆周运动

问题3.如图3所示，小物块放在旋转圆台上，与圆台保持相对静止，如图所示，物块与圆台间的动摩擦因数为μ，离轴距离为r，圆台对小物块的静摩擦力(设最大静摩擦力等于摩擦力)提供小物块做圆周运动所需的向心力。求：圆台转动的最大角速度？

通过小组互助合作探究，现展示讨论结果如下：

问题1展示：

受力分析如图4所示

小球的向心力由T和mg的合力提供

F向=F=mgtanθ

小球做圆周运动的半径R=Lsinθ

由牛顿第二定律：F=ma=mω2R 即 mgtanθ=mω2R

问题2展示：

解析：小橡皮受力分析如图。

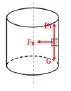
小橡皮恰不下落时，有：

Ff=mg 其中：Ff=μFN

而由向心力公式：FN=mω2r

问题3展示：由于小物块做匀速圆周运动

静摩檫力提供向心力f静= mω2r

要使圆台转动的角速度达到最大，静摩檫力要达到最大静摩擦力

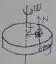
Fmax=μmg，μmg = mωmax2r

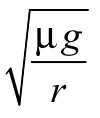
（三）学生讨论，小组互助合作，教师点评总结

根据各小组展示的情况，下面由教师作以下总结，以上问题同学们都能很好的画出受力分析图，并且对向心力的来源分析的很到位，下面总结物体做匀速圆周运动的一般解题步骤1.四确定：确定研究对象、确定轨道平面、确定圆心位置、确定向心力的方向。

2.受力分析。3.分析向心力的来源。4.选定向心力方向列方程求解。

下面同学们再思一个问题，在问题3中，如果增大圆盘转动的角速度，小物块会做什么运动呢？此问题与临界问题有关。下面我们一起来探讨一下与静摩擦力有关的临界问题。

问题4.如图示，水平转台上放有质量均为m的两个小物块A、B，A离转轴中心的距离为L，A、B间用长为L的细线相连。开始时，A、B与轴心在同一直线上，细线刚好被拉直，A、B与水平转台间的动摩擦因数均为μ，最大静摩擦力等于滑动摩擦力，求：

(1)当转台的角速度达到多大时细线上开始出现张力？

(2)当转台的角速度达到多大时A物块开始滑动？

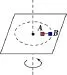
(2)当物块A刚要开始滑动时，A、B受到的静摩擦力都达到最大值，设此时细线上的张力为F，根据牛顿第二定律

对A，有μmg－F＝mω22rA，rA＝L

对B，有F＋μmg＝mω22rB，rB＝2L

对于临界问题的分析可以总结为：物体间恰好不发生相对滑动的临界条件是物体间恰好达到最大静摩擦力，如果只是摩擦力提供向心力，则有Ffm＝mv2/r，静摩擦力的方向一定指向圆心。

总之,这种教学方法的优势是明显的：我们通过问题导入，学生自主思考，老师引导；小组合作探究，展示成果以及教师点评总结的教学思想，可以提升学生的发散性思维和总结归纳物理模型的能力。通过小组互助合作学习，发挥群体的集体智慧并且提高各小组成员的积极功能，从而激发个体的学习动力和提高能力，并且组内成员互相协作、发挥各自优势，取长补短，既完成了特定的教学任务又达到了培养学科素养的目的。通过这种“问题导入式+小组互助合作”教学模式，可以提升学生的参与度，发挥学生在课堂中的主体地位，从而提高学生的学习效果，进而使课堂效率最大化。