无控制条件下机载LiDAR航带拟稳平差方法

, , ,

(1.武汉市国土资源和规划信息中心，武汉 430014;2.湖北大学 资源环境学院，武汉 430062

0 引言

机载激光雷达(airborne laser radar，LiDAR)作为一种空间测量系统，其对地定位精度受到内外在多种因素的综合影响，并会有系统误差产生[2-3]。国内外学者对无控制条件下的航带平差技术进行了大量研究：一种是基于数据驱动的无控制航带平差，这类航带平差将机载LiDAR中的各个误差的综合影响看做是航带的各种形变，以单独某条航带作为基准或以多条航带间共轭点的平均坐标作为基准，对点云数据坐标进行变换改正，从而减小相邻航带同名特征之间以及点云数据与对应的实际控制点之间的三维偏移[4-9]。这类方法受基准选取因素的影响较大，可能造成误差的累积效应[10]。另一种是基于模型驱动的无控制航带平差，这类航带平差将机载LiDAR中最主要的误差来源——安置角误差等作为模型求解改正参数，以航线飞行轨迹作为基准，进行航带的自检校[11-15]。这类方法依赖航迹信息的POS精度，很难补偿或改正由于POS系统导致的系统偏差。为此，本文借鉴基础测绘领域拟稳平差[16]思想，提出了一种无控制条件下的机载LiDAR数据航带拟稳平差方法，探讨了该方法对提高点云数据质量精度的有效性。

1 算法流程

该方法基本思想是：在航带平差前后，测区整体的重心稳定不变，翻转幅度为零，扭曲系数为零，即拟定测区整体的重心和形变程度“稳定”。具体流程方法如图1。

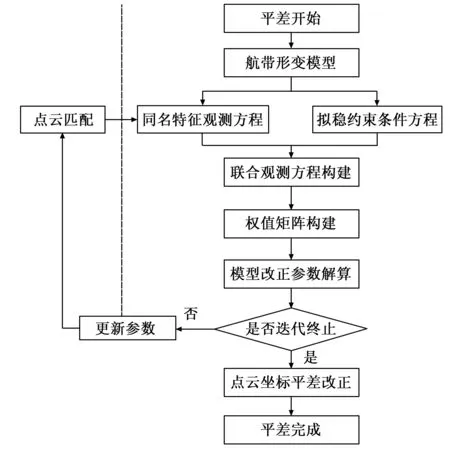
图1 平差流程图

1.1 航带形变模型构建

(21)

式中，ΔX、ΔY为航带的水平坐标改正参数，a、b、c、d为航带高程在旁向上的线性改正及航向上的非线性改正参数。

对应航带点云的改正方程为：

(2)

式中，x,y,z为该航带点云的原始坐标，x改,y改,z改为点云经过航带形变模型纠正后的坐标，ΔH(U,V)=aU+bV2+cV+d为高程坐标改正，其中U、V为点云在该航带坐标系中的坐标，如图2所示。

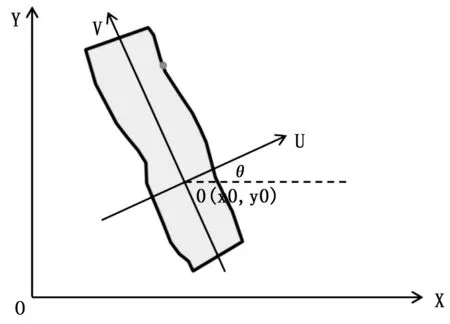
图2 航带坐标系与地理坐标系间的关系

点云在航带坐标系下的水平坐标(U,V)与在地理坐标系下的水平坐标(X,Y)之间的相互转换关系如下：

(3)

式中，θ为航带航向与Y轴正方向的夹角，x0、y0为航带几何中心的水平坐标。

1.2 航带拟稳约束条件构建

1.2.1 无控制航带平差秩亏数

在仅存在连接特征作为观测值且连接特征分布均匀、数量足够的情况下，由于缺少必要起算条件，组成的观测方程的系数矩阵B观为秩亏矩阵：

V观=B观X-L观

(4)

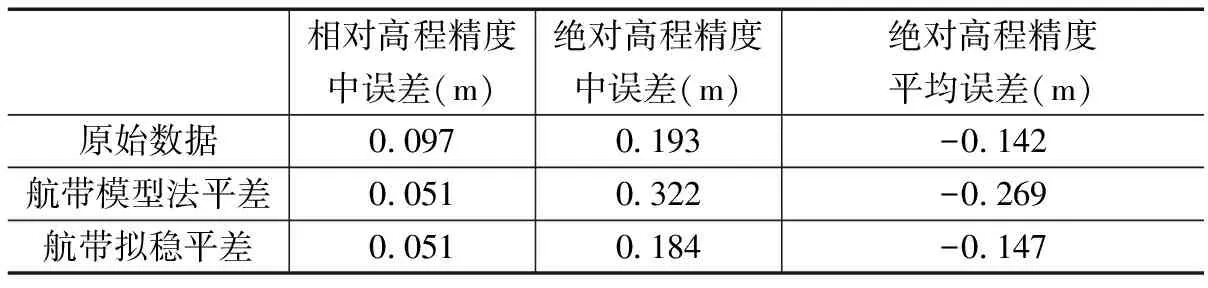
R(B观)=t0

(5)

式中，t为系数矩阵列数。

即，该系数矩阵的秩亏数为6。为此，本文讨论的拟稳约束条件共有6组，用于拟稳航带平差。

1.2.2 拟稳约束条件构建

(1)拟稳约束条件①和②。

约束原理：平差后的测区整体在水平方向上的重心位移为0。

①和②以观测方程的形式可表达为：

VΔX=ΔX1·P1+…+ΔXi·Pi+…+ΔXn·Pn

(6)

VΔY=ΔY1·P1+…+ΔYi·Pi+…+ΔYn·Pn

(7)

式中，VΔX,VΔY为测区整体偏移的观测值，ΔXi，ΔYi为第i个航带形变模型中的水平改正参数，Pi为第i个航带的拟稳权值(见1.2.3小节)。

(2)拟稳约束条件③。

约束原理：平差后的垂直方向上的重心位移为0。

③以观测方程的形式可表达为。

VΔZ=ΔZ1·P1+…+ΔZi·Pi+…+ΔZn·Pn

(8)

式中，ΔZi为第i条航带的平均垂直重心位移。

设该航带宽lui，长lvi，则ΔZi可下式计算：

ΔZi·SD=∬DaiU+biV2+ciV+didUV

(9)

即：

(10)

解得：

(11)

将上式代入公式(28)得整体测区在垂直方向上的重心位移的观测方程。

(3)拟稳约束条件④和⑤。

约束条件④原理：平差后的整个测区以其重心为中心饶Y轴负方向的旋转系数为0，即平差后整个测区以x正方向为力臂方向，以重心为旋转中心的高程偏移的一阶矩Mx应为0。

Mx可表达为：

Mx=M1x·P1+…+Mix·Pi+…+Mnx·Pn

(12)

式中，Mix为第i条航带的高程偏移一阶矩。

仍设该航带宽lui，长lvi，则Mix可下式计算：

Mix=∬D(aiU+biV2+ciV+di)xdUV

(13)

式中，x为航带上一点到测区重心在x方向上的距离。

将公式(23)代入上式，则有：

(cosθi·U-sinθi·V+x0i)dUdV

(14)

解得：

(15)

同理，约束条件⑤原理：平差后的整个测区以其重心为中心饶X轴正方向的旋转系数为0，即平差后整个测区以y正方向为力臂方向，以重心为旋转中心的高程偏移的一阶矩My应为0。

My可表达为。

My=M1y·P1+…+Miy·Pi+…+Mny·Pn

(16)

式中,Miy为第i条航带的高程偏移一阶矩。仍设该航带宽lui，长lvi。

解得：

(17)

再进一步消除旋转系数观测值与高程偏移一阶矩之间的量纲差异，则公式(12)和(16)以观测方程的形式分别表达为：

(18)

(19)

(4)拟稳约束条件⑥。

约束原理：平差后的整个测区扭曲系数之合为0。

⑥以观测方程的形式表达为。

VR=R1·P1+…+Ri·Pi+…+Rn·Pn

(20)

式中,Ri为航带i的扭曲系数。

由于航带产生形变的受航带形变模型改正参数b的影响，仍设该航带宽lui，长lvi，则Ri可按下式计算：

(21)

将上式代入公式(20)，则为拟稳约束条件⑥的完整表达式。

根据拟稳基准构建上述6组拟稳约束条件后，即可用于解求基于无控制航带拟稳平差的最优解。

1.2.3 航带拟稳权值设定

拟稳权值反映了各个航带对整体拟稳基准的贡献程度，可根据各个航带获取的点云质量酌情设置。

如果各个航带由同一架次飞机获取，那么，各个航带对平差基准的贡献权值Pi可按等权分配，即：

P1=P2=……=Pn=1

(22)

如果某条航带在飞行时，出现GPS信号失锁等突发状况导致其点云获取精度降低时，可将其从平差基准中剔除，即：

Pi=0

(23)

如果各个航带飞行条件不同时，例如：不同架次、不同航高、不同设备等，可根据各航带的具体航飞参数设定不同权值。

特殊的，如果将某一条航带以外的其他航带权值设为0，即：

Pj=1,Pi=0(i=1,2,…,n且i≠j)

(24)

此时上述情况转变为航带模型法平差，即以某一条航带为基准改正其他航带。

1.3 平差模型求解计算

(1)联合观测方程构建。

利用点云三维表面匹配技术得到同名特征对，构建同名特征观测误差方程组：

V观=B观X-L观

(25)

利用拟稳约束条件的构建策略，构建拟稳约束观测方程组：

V拟=B拟X-L拟

(26)

联立上述公式(25)(26)构建联合观测方程组：

V=BX-L

(27)

(2)权值矩阵构建。

匹配的同名特征观测值的权值Pi主要根据其匹配相似度估计，具体计算方法依匹配算法而定，但需使Pi∈[0,1]，而后构建同名特征的权值矩阵P观：

(28)

拟稳约束条件作为航带平差中的基准，其观测误差的权值应远大于同名特征匹配点的权值，可设定为10000，即:

P拟=10000E

(29)

联合上述公式(28)(29)求得权值矩阵P。

(30)

(3)模型改正参数解算。

根据联合观测误差方程(27)和权值矩阵(30)，利用最小二乘原理解算方程系数向量X：

X=(BTPB)-1BTPL

(31)

(4)迭代终止条件。

平差迭代的终止条件为：1)平差改正前后的航带形变模型改正值的变化量足够小，这里以实验中的经验确定。2)最大迭代次数。本文航带拟稳平差模型收敛速度较快，设定的最大迭代次数为5。

2 实验分析

2.1 对检校场测区数据的实验

实验数据一来自中国敦煌市区4×0.8 km2大小的检校场区域，该测区包含两条东西向相向飞行的航带数据，飞行轨迹近似重合，其相对航高约为800 m，测区整体概况如图3所示。

图3 敦煌市区检校场点云数据

该实验数据为系统检校前的点云数据，具有明显的系统误差。主要表现为：

(1)航带两侧存在较大高程差，航带边缘处高差可达0.60 m。

(2)航带间在存在明显水平偏移，东西偏移近2.2 m，南北偏移近0.8 m。

图4 剖面截取位置与方向

图5 平差前测区局部细节剖面图

采用本文拟稳平差模型进行平差解算，两条航带的拟稳权值均设为1，得到2个航带形变模型改正参数，如表1所示。

由表1可知，两航带水平坐标改正幅度相同，在旁向上的高程坐标改正系数一致，航向上的高程坐标基本不变。

利用改正参数对点云进行坐标改正，测区局部细节效果如下所示。

表1 各航带形变模型改正参数值

图6 平差后测区局部细节剖面图

由图6可知，航带间的相对偏移被消除，同名地物吻合情况良好。

为进一步验证上述平差结果对绝对精度的影响，又对该组数据做了严格的系统检校，并以系统检校后的点云作为参考点云与平差结果点云进行比对。两者实验结果的局部细节的比对如图7所示。

图7 拟稳平差与系统检校结果比对

由图7可知，平差结果点云与参考点云吻合情况良好。对上述实验结果进行精度评定，评定结果如下表。

分析表2可知，经过拟稳平差后的点云数据，航带间的偏移被消除，相对精度大大提高；此外，平差结果与参考点云间相对偏移量极小，间接说明了拟稳平差后点云的绝对精度也得到了提升。

表2 原始数据、航带平差、系统检校结果精度评定

2.2 对大范围测区数据的实验

为进一步验证航带拟稳平差对大范围测区数据的实用性，以及相较经典航带模型法平差在抑制误差累积方面的有效性。选取了实验数据二进行实验，该数据来自于美国Niagara地区，包含来回飞行的五条航带，相对航高约1 000 m，并有若干个地面高程控制检查点，尽管该数据经过检校后数据质量已经达标，但仍存在少量残余系统误差。测区整体概况如图8所示。

图8 Niagara测区点云数据

首先采用经典航带模型法平差，在无控制点条件下以航带1为基准(即航带1的改正参数设定为0)进行平差实验。而后采用本文拟稳平差模型进行平差解算，航带拟稳权值均设为1。最后，选用若干处于平坦地面(如马路、停车场)上的高程控制点作为检查点。对上述两种实验结果进行了精度评定，评定结果如表3所示。

表3 不同平差方法下的精度比较

由上表可知，采用经典航带模型法平差方法，尽管相对精度有所提高，但由于基准航带为单挑航带并存在翻滚角误差，在平差过程中产生了累积效应，整体高程发生一定程度的漂移，绝对精度反而降低。而采用本文航带拟稳平差方法，受拟稳约束条件的约束，航带间的累积误差得到很好的抑制，而且随着相对精度的提高，绝对精度也有所提高。

3 结束语

文章归纳分析了现阶段机载LiDAR数据航带平差的主流方法的优劣，并提出了本文研究方法的思路。首先介绍了本文航带平差方法采用的航带形变模型，然后提出了航带拟稳平差模型，推导了航带拟稳平差约束条件，最后利用两组典型的测区数据进行了航带拟稳平差实验，并与严格系统检校结果、经典航带模型法平差结果进行了对比。实验结果表明，该方法能够有效减弱或消除机载LiDAR数据的系统误差，同时抑制航带平差过程中累积误差的产生，从而提高点云数据的质量和精度。