《2.7有理数的乘法(第1课时)》教学设计

广东省清远市佛冈县城东中学 冯连金

一、教学目标

1.知识与技能目标：了解倒数的概念，理解有理数乘法法则，会进行有理数的乘法运算

2.过程与方法目标

①在实际背景和计算中探索出有理数乘法法则，培养学生的合作与探究意识，提高学习兴趣。

②经历探索有理数乘法法则的过程，发展学生的观察、分析、归纳、猜测、验证等能力。

3.情感与价值观目标：合作交流中，积极思考，主动参与，形成良好的学习习惯

二、教学重点、难点、教学关键

教学重点：理解有理数乘法法则，会进行有理数的乘法运算，掌握积的符号的确定方法；

教学难点：有理数乘法中积的符号的确定方法

教学关键：掌握有理数乘法运算的符号确定方法

三、教学方法和手段

1.课前准备：教学课件，学生课前预习

2.教学方法：启发式教学法、探究发现法，合作学习法

3.教学媒体：电教平台，实物投影仪

四、教学过程

（一）创设情境，发现新知

（二）合作交流，新课探究

一是探索猜想，归纳法则

1.（教科书P49“议一议”）计算下列各题

(-3)×4 =-12

(-3)×3 = ___；

(-3)×2 = ___；

(-3)×1 = ___；

(-3)×0 =___。

议一议：观察以上算式，一个因数减少1时，积怎样变化?

2.（教科书P49“议一议”）按照上述规律，你能写出下列算式的结果吗

(-3)×0 = 0

(-3 )×(-1 ) = __；

(-3 )×(-2 ) = __；

(-3 )×(-3 ) = __；

(-3 )×(-4 ) = __。

议一议：观察每个式子，你能得到什么结论?

3.有理数乘法法则

教问：从上面的8个乘法的算式中，你能总结有理数的乘法法则吗？

生：分小组讨论，合作交流，尝试用简洁的数学语言描述有理数乘法的法则。

师：（1）给出问题，让学生分组讨论，鼓励学生自己总结，用适当的语言描述；

（2）参与小组的活动，发现学生碰到困难，适当引导，及时肯定、鼓励；

（3）投影显示有理数乘法法则

两数相乘，同号得正，异号得负，并把绝对值相乘。

任何数与0相乘，积仍为0。

教师明确指出：两数相乘，同号得正，异号得负，注意不可与有理数加法的符号法则混淆。

二是验证法则，掌握规律

1.（小试牛刀）口算

①(-2 )×(-3 ) = __；②4 × (-2 ) = __；

③(-5)×0 =__； ④(-1 .2)×(+3 ) = __；

学生活动：口答结果

教师活动：引导学生概括计算方法。

归纳：计算方法：先确定积的符号，再确定积的绝对值。

2.（教科书P50）例1：计算

（1）(-4)×5(2)(-5 )×(-7)

学生活动：学生独立计算

教师活动：指名学生到黑板演示，巡视学生练习情况，及时引导学生明确算理，师生共同评析，明确指出解题格式的书写规范。

师：请同学们观察：上面的第（3）、（4）小题的两个因数与积有什么特点？

3.倒数的概念

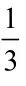
4.（我学我会）练习：

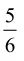
学生活动：学生归纳倒数的概念，完成练习

教师活动：明确倒数的概念，求倒数时，小数要先化成分数再求，带分数先化成假分数。

（三）巩固新知，拓展新知

1.（教科书P50）例2：计算（1）(-4 )×5 × (-0.25)

学生活动：学生尝试独立完成计算，遇到困难可以同桌讨论。

教师活动：①指名板演，教师个别辅导，学生完成后，师生共同评价，要使学生明确，有理数相乘时，先确定积的符号，再确定积的绝对值。

②引导学生观察算式，猜想积的符号与因数的有什么关系。

2.(探究辨识)计算下列各式

(-1)×2× 3× 4 = ____；（有1个负因数，积是负数）

(-1)×(-2 )×3× 4 = __；（有2个负因数，积是正数）

(-1)×(-2 )×(-3 )×4 = __；（有3个负因数，积是负数）

(-1 )×(-2 )×(-3 )×(-4 ) = __；（有4个负因数，积是正数）

(-1)×(-2 )×(-3 )×(-4 )×0 = __。（有一个因数为0，积为0）

找一找：积的符号与什么因数有关。

3.提出问题：（教科书P51 “议一议”）几个有理数相乘，因数都不为零时，积的符号怎样确定？有一个因数为0时，积是多少

（1）几个数不为0的有理数相乘，积的符号由负因数的个数决定，当负因数有奇数个时，积的符号为负；当负因数有偶数个时，积的符号为正。（2）只要有一个因数为0，积就为0。

4.用先确定积的符号的方法计算例2

（1）(-4 )×5×(-0.25)

学生活动：独立计算

教师活动：让学生先确定积的符号，再进行计算，完成后引导学生与前面所做的例2计算比较，让学生感受算法的不同。

（四）随堂练习，学以致用

1.计算

2.冬冬在A地西面10千米处，每小时向东行走6千米，那么3小时后，他在A地东面还是西面且距A地多少千米

（五）总结反思，拓展升华

这节课你有什么收获？有什么体会？

1.有理数的乘法法则

两数相乘，同号得正，异号得负，并把绝对值相乘。

任何数与0相乘，积仍为0。

2.计算方法：先确定积的符号，再确定积的绝对值。

3.倒数的概念：如果两个有理数的乘积为1，那么称其中一个数是另一个数的倒数，也称这两个数互为倒数。

4.几个有理数相乘的积的符号的确定方法：

（1）几个不为0的有理数相乘，积的符号由负因数的个数决定，当负因数有奇数个时，积的符号为负；当负因数有偶数个时，积的符号为正。

（2）只要有一个因数为零，积就为零。

（六）课堂反馈，检查效果

（七）布置作业，课外延伸

1.必做题：教科书P51习题2.10：知识技能1

2.选做题：教科书P52习题2.10：问题解决3