复杂近地表探区静校正量的地表一致性融合技术

王立歆,林伯香

(中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)

静校正是对近地表速度和高程的横向变化所做的时间校正,以使采集的地震数据近似地符合多次覆盖处理技术的要求[1-2]。依据静校正的基本理论,假设在可以起伏的地表面下存在厚度和速度横向可以变化的低速带、低速带下是一个速度横向不变的高速层,静校正量等于剥离(减去)地表面下的低速带到低速带底(高速层顶)界面所需时间和用高速层速度(替换速度)填充(加上)从高速层顶界面到最终基准面所需时间之和,具有地表一致性的特点。

一个工区完整的静校正一般由基准面静校正和剩余静校正2个部分组成。基准面静校正基于近地表速度模型,计算过程包括了近地表速度模型建模和基于所建立近地表速度模型的静校正量的计算2个步骤,是对近地表速度模型和高程横向变化的校正。不同基准面静校正方法的区别主要在近地表速度模型的建模方法[3],它们基于对速度模型的不同假设,得到有差异的近地表速度模型,例如:基于折射模型的方法[4-5]将得到层状近地表速度模型,基于初至层析技术的方法[6-8]将得到纵横向速度可变的近地表速度模型等等,它们有各自的适应性。初至层析静校正方法被认为是目前适应能力最强的静校正方法。

剩余静校正是对基准面静校正的补充。剩余静校正的过程依次可以包括基于初至时间的多域迭代剩余静校正和基于反射能量统计的反射剩余静校正等。多域迭代剩余静校正用于初步解决近地表速度模型和测量数据的误差产生的静校正量,计算的静校正量不受地震信号1/2周期的限制。反射剩余静校正是对反射时间的进一步精细校正,需要进行剩余静校正量计算和叠加速度分析的多轮迭代。反射剩余静校正量的计算还可以进一步采用分频技术,依次解决针对低、中、高频段地震信号的精细校正问题。牛琳等[9]给出了剩余静校正的典型过程。

基准面静校正是整个静校正过程的基础,在基准面静校正量准确的情况下,各种剩余静校正才有意义。然而,对于复杂近地表地区,近地表条件的复杂性已经远超静校正方法的假设前提,基准面静校正的合理性受到质疑。崔庆辉等[10]给出了对静校正技术的看法、试验了波场延拓近地表校正技术,认为在复杂地表区静校正技术已经不再适用,波场延拓近地表校正技术在理论模型上可以取得很理想的效果,但在实际资料应用中由于无法得到准确的近地表速度模型而效果不理想。王华忠等[11]认为,在山前带等复杂探区,理论上根本不存在静校正问题,只存在近地表建模与叠前深度偏移问题,因为在已知包括近地表速度模型的准确速度模型的基础上,现有起伏地表偏移技术可以解决复杂的近地表问题。

地震勘探工区实际近地表速度模型客观存在,只是当今还没有办法获得。现有层析技术得到的近地表速度模型只是实际近地表速度模型的近似结果。将由层析技术得到的近地表速度模型应用于起伏地表深度偏移速度建模,有望改善深度偏移的精度[12-13],但要解决好实际近地表速度模型和层析近地表速度模型之间差异部分的校正问题,这种校正现在还是以高频道间时差即高频静校正量的方式实现,高质量的常规静校正处理是计算这种高频静校正量的前提。

在复杂近地表区,我们试图开辟新的技术路径以避开对静校正技术的应用,但在无法得到准确近地表速度模型的现有技术条件下,静校正技术所发挥的作用一点也没有减少。相对于复杂的实际近地表条件,现有的各种静校正方法都是一种近似,不同的方法针对不同近地表条件近似程度不同,关键是要找到近似程度相对最好的。

当前被认为适应能力最强的初至层析静校正方法,其适应性主要表现在近地表速度模型的建模部分,能够适应相对复杂的近地表条件,但层析建模结果还受所用初至信息偏移距范围等参数的影响。在取得近地表速度模型的基础上,初至层析静校正方法中的静校正量计算还需要剥离底界和替换速度等参数,即使是同一个近地表速度模型,不同的剥离底界和替换速度参数可以得到差异很大的基准面静校正量。在南方山地等复杂近地表地区,一般情况下并不存在横向速度不变的高速层,所谓高速层的速度横向上往往有很大的变化,难以选择一个适合整个工区的替换速度,存在针对工区的不同部分采用不同剥离与替换速度的情况[14]。可见在一个不同区域近地表条件明显差异的复杂工区,同一个层析静校正方法针对不同区域,合适的层析反演和静校正计算参数也应该是不一样的,决定静校正量及其应用效果的不仅仅是静校正方法,还取决于速度建模和静校正计算所用的参数。

现有不同的层析静校正软件,计算的静校正量基本上都是基于近地表速度模型的基准面静校正量和基于初至时间的多域迭代剩余静校正量之和,不同的近地表条件下这2个静校正量有可能具有各自的优势。

基于上述事实,在复杂近地表条件地区,可能一种静校正方法和参数计算的一个静校正量适合工区的一个部分,而依据另一种静校正方法或者相同静校正方法不同参数计算的另一个静校正量适合工区的另一部分,也可能一个静校正量在高频成分方面较有优势而另一个静校正量在中低频成分方面较有优势,难以通过调整参数使一种静校正方法与参数得到对整个采集工区都有较好的结果。不同静校正量的优势互补成为我们的必然选择。

现有地震处理软件系统所设计的静校正量应用流程所包含的、以及研究人员所提出的对不同静校正量的优势互补技术基本上都是一种非地表一致性的技术,都是把静校正量分解成CMP域的长波长成分(也称CMP面时间)与道域的短波长成分并进行融合[15-16],我们称其为静校正量的常规融合技术。首先分别将2个静校正量分解成CMP域的长波长成分(即一个CMP一个值)与道域的短波长成分(即一个地震道一个值)。这种分解后的长波长成分决定叠加剖面的构造形态,短波长成分主要影响地震剖面的叠加效果。然后取其中一个静校正量的CMP域长波长成分作为融合后的长波长成分,2个静校正量的短波长成分依据各自静校正量叠加剖面的优势区域进行拼接以得到融合后的短波长成分。相当于在分别将2个静校正量应用于地震资料处理得到2个叠加剖面的基础上,取其中一个静校正量的CMP域长波长成分为标准,对应用另一个静校正量的叠加剖面进行时移,时移量等于2个静校正量的CMP域长波长成分之差,然后对时移后的叠加剖面按其叠加优势区域拼接到未时移的那个叠加剖面上。可见,第一,静校正量的常规融合技术是对不同静校正量叠加剖面进行时移后的拼接,仅仅实现了对应用各自静校正量所得的叠加结果的优势互补,并未完全实现对各自静校正量的优势互补(本文将结合实例阐明,应用真正实现了各自静校正量优势互补的静校正量的叠加结果,将会好于这种常规融合技术所得到的叠加结果);第二,最终应用于地震数据的静校正量不是地表一致性的,道集成果数据中不存在所应用的地表一致性总静校正量的信息,该信息对道集成果数据的进一步处理和应用非常重要。

本文给出一种具有地表一致性特点的、可以实现对静校正量进行分频段和分区域融合的方法,并以实际数据的应用展示了该方法的应用思路和效果。

1 方法原理

每一个静校正量都包括了炮点和接收点静校正量2部分,本文方法对炮点静校正量和接收点静校正量采用相同的方法分别处理,故在方法原理的说明中不区分炮点和接收点的静校正量,仅笼统地指某一个静校正量。2个不同的静校正量可以对应2个不同静校正软件和参数,也可以对应相同静校正软件和不同参数计算的静校正量。

假设依据炮点和接收点范围确定的工区最大平面坐标范围为集合A;假设有2个不同的静校正量,第1个静校正量为t1(x,y),第2个的静校正量为t2(x,y);假设根据对2个静校正量叠加剖面的对比,第1个静校正量在控制整体构造形态上有优势,而第2个静校正量在集合B表示的平面坐标范围内在局部构造形态或叠加效果(取决于静校正的中波长或短波长成分的准确性)方面具有优势,且假设集合B是一个连通的闭合区域,显然集合B是集合A的子集。

依据集合B的范围计算第2个静校正量的权系数w2(x,y)。将集合A所含的整个区域分成3个部分:①过渡区,即集合B边界附近离边界一定距离(过渡区长度的一半)范围内的环状条带区;②优势区域核心区,即集合B范围除去过渡区外的部分;③其它区域,即整个工区除上述2个区域以外的部分。优势区域核心区的权系数为1.0,其它区域权系数为0,过渡区的权系数从优势区域核心区与过渡区交界处的1.0逐渐减少到过渡区与其它区域交界处的0。图1 是优势区域及权系数的示意图,上、下、左、右4个坐标轴所围合的整个区域为工区的最大范围即集合A,充填图案为红色斜线的区域为优势区域核心区(权系数为1.0),充填图案为蓝色斜线的区域为其它区域(权系数为0),绿色和黄色区域分别为过渡区中权系数在(0,0.5)和(0.5,1.0)区间内的部分,权系数为0.5的等值线和右侧坐标轴所围合的区域(黄色与红色斜线区)是第2个静校正量的优势区域即集合B。

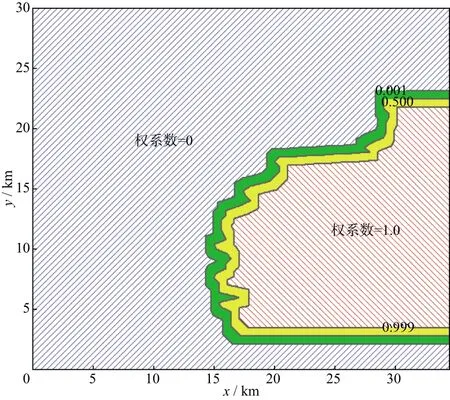
图1 优势区域及权系数示意

1.1 静校正量地表一致性分解

视具体情况,可以将静校正量只分解成长波长与短波长2个频段的静校正量,也可以分解成长波长、中波长和短波长3个频段的静校正量。平滑滤波是进行这种分解的简单方法。如果仅分解成长、短波长2个频段的成分,静校正量为:

(1)

如果分解成长、中、短波长3个频段的成分,静校正量为:

t1(x,y)=t1L(x,y)+t1M(x,y)+t1S(x,y)

t2(x,y)=t2L(x,y)+t2M(x,y)+t2S(x,y)

(2)

式中:下标L,M,S分别表示长、中、短波长成分。

1.2 静校正组合

如果静校正量只分解成长、短波长2个成分,组合后的长波长成分取第1个静校正量的,按照第2个静校正量的权系数组合2个静校正量的短波长成分:

(3)

如果静校正量分解成长、中、短波长3个成分,组合后的长、短波长成分取第1个静校正量的,按照第2个静校正量的权系数组合2个静校正量的中波长成分:

(4)

上述分解成长、短波长2个频段,或者分解成长、中、短波长3个频段的波长边界,与常规静校正所述的以排列长度为基准的长、短波长分界既有联系,又有区别。需要结合对叠加剖面的分析和解释人员的意见加以确定。

我们这里把对不同静校正量叠加剖面的对比评价简化成构造形态和叠加效果2个方面,构造形态还可以分成全局构造形态和局部构造形态,叠加效果是指CMP道集的同相性导致的(局部)叠加剖面同相轴的清晰度。假设对应用2个静校正量的叠加剖面对比结果表明,第1个静校正量的叠加剖面在控制整体构造形态上有优势,而第2个静校正量的叠加剖面在某些平面范围内叠加效果具有优势,可以选择分解成2个频段的融合方法;如果对比结果表明,第1个静校正量的叠加剖面在整体构造形态上较合理,叠加效果较好但在某些平面范围内局部构造形态不合理(比如同相轴存在串相位现象),而第2个静校正量的叠加剖面在对应平面范围内局部构造形态相对更合理(比如同相轴串相位现象不存在或相对不严重)但

叠加效果相对差一些,表明第2个静校正量的中频段成分在该平面范围内具有优势,可以选择分解成3个频段的融合方法。

在实际资料处理的静校正测试过程中,可能有多于2个的静校正量表现出各自的优势,各个静校正量的优势区域也可能不如上述所假设的那么简单。第2个静校正量叠加效果的优势区域有可能是多个不连通的区域,也可能在第2个静校正量的较大范围的优势区域内部还存在第1个静校正量叠加效果相对更好的区域,也可能尽管在整体趋势上第1个静校正量的构造形态合理但在某些区域内第2个静校正量的构造特征更加合理且第1个静校正量的叠加效果更好,等等。所有这些复杂的情况,都可以分解成上述简单情况的不同组合。

2 应用实例

给出南方山地地区2个应用实例。实例1由于出露地表的岩性表现出明显的分区,导致适用的静校正方法也表现出明显的分区特征,将静校正量分解成长、短波长2个频段进行融合。实例2中存在的隆起于地表的背斜构造导致近地表速度模型和静校正计算的复杂性,第2个静校正量的中频段成分具有优势,将静校正量分解成长、中、短波长3个频段进行融合。

2.1 实例1

南方山地三维工区近地表地形起伏剧烈,表层岩性平面上大致可分成2个区域,一个是占工区较大范围的以砂岩地层为主的区域(砂岩区),一个是占工区约1/3的灰岩出露区域(灰岩区)。近地表速度差异较大,存在明显的分区性,图2是采用初至层析近地表建模技术得到的砂岩和灰岩过渡区的近地表速度模型。

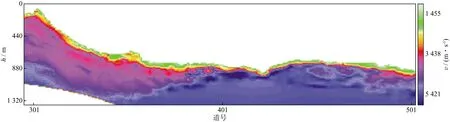
图2 砂岩与灰岩过渡区的近地表速度模型

多种静校正方法和参数的测试结果表明,有2个静校正量分别在砂岩区和灰岩区具有各自明显的优势。其中,第1个静校正量在砂岩区叠加效果具有明显的优势,且叠加剖面上的构造形态在整个工区相对较合理;第2个静校正量的叠加效果在灰岩区具有明显的优势。

图3和图4分别是在砂岩和灰岩区过渡带应用第1个和第2个静校正量的叠加剖面,从中可以容易划分出各自优势区域的边界,边界左侧是砂岩区,右侧为灰岩区。

图3 应用第1个静校正量后的叠加剖面(实例1)

图4 应用第2个静校正量后的叠加剖面(实例1)

从叠加剖面上拾取第2个静校正量对叠加效果有优势的区域在平面上的分布,构成第2个静校正量的优势区域。和整个工区的最大平面坐标范围一起计算第2个静校正量的权系数w2(x,y)。

对一个CMP点而言,以该CMP点为中心直径在一个有效偏移距范围内的属于该CMP的所有地震道的炮点和接收点的静校正量,都可能对该CMP的叠加结果有影响。当一个工区的近地表条件存在明显的分区性,并导致2个静校正量的精度存在明显的分区性的情况下,只要各分区的大小明显大于有效排列长度,必然导致叠加结果的分区性且叠加结果的分区与静校正精度的分区相一致,依据叠加结果拾取的分区边界,可以代表2个静校正量精度的分区边界。

分别将2个静校正量分解成长、短波长2个频段的成分。经与解释人员一起分析试验,确定区分长、短波长2个频段的波长边界取6000m,即波长大于6000m的成分属于决定剖面构造形态的“长波长”,其它成分属于主要影响叠加效果和局部构造形态的“短波长”。事实上,这里的“短波长”成分与常规静校正所述的短波长成分不完全一样,还包含对叠加剖面局部构造形态有影响的成分。

依式公式(3)计算融合后的静校正量,应用于地震资料处理得到如图5所示的结果。

图5 应用融合静校正量后的叠加剖面(实例1)

对比图3,图4和图5可以看出,应用融合静校正量后(图5)的构造形态达到了预期目的即取第1个静校正量的,叠加效果不仅是取2个静校正量的各自优势,而且是优于2个静校正量的各自叠加效果的优势之和,特别在优势区域边界附近。这是地表一致性的融合方法才会有的效果。事实上,第1个静校正量在优势区域边界左侧的精度较高但右侧精度相对不够,第2个静校正量则相反在优势区域边界右侧精度较高而左侧精度相对不够。图3优势区域边界左侧附近的叠加结果,除了受边界左侧较高精度静校正量影响外,还受边界右侧相对较低精度静校正量的影响,即决定图3边界左侧附近叠加结果的静校正量一半具有较高精度一半相对精度不够。同样,图4优势区域边界右侧附近的叠加结果,除了受边界右侧较高精度静校正量影响外,还受边界左侧相对较低精度静校正量的影响,即决定图4边界右侧附近叠加结果的静校正量一半具有较高精度一半相对精度不够;融合后的静校正量在优势区域边界左右2侧都有较高的精度,导致图5在优势区域左右2侧的叠加效果分别远好于图3左侧和图4右侧的结果。图3到图5的叠加剖面是在动校正后的数据上替换应用各自的静校正量得到的,后续处理还需针对融合静校正量进行叠加速度的分析。

如果使用静校正量的常规融合技术,只能实现2个静校正量叠加剖面的时移拼接,即应用常规融合静校正量后的叠加效果不可能好于融合前2个静校正量的各自叠加效果的优势之和。

2.2 实例2

南方山地某三维工区静校正的难点在于其中存在的一个背斜构造区域,该背斜构造在地表隆起形成一个山脉,构造顶部地层断裂、破碎并被剥蚀,不同的静校正方法在该区域表现各异。图6是利用初至层析近地表建模技术得到的近地表速度模型,构造高点处速度结构复杂。

多种静校正方法和参数得到的多个静校正量的试验结果对比,筛选出了最具优势的2个静校正量,称为第1个静校正量和第2个静校正量。对分别应用2个静校正量并经一次剩余静校正后得到的整个工区2套叠加剖面的对比得出这样的基本认识,即应用第1个静校正量在整体构造形态上较合理,多数剖面段叠加效果较好,但在背斜构造核心部位同相轴存在较多的断断续续现象;应用第2个静校正量在背斜构造核心部位同相轴的断续现象明显减少,但有些剖面段叠加效果相对差一些。第1个静校正量和第2个静校正量并不存在明显空间上的分区优势。

图7和图8分别是应用第1个静校正量和第2个静校正量,并经一次剩余静校正后在背斜构造核心区域及附近的叠加剖面,这两个剖面代表了整个工区2个静校正量的应用结果在背斜构造核心区的大致差别。

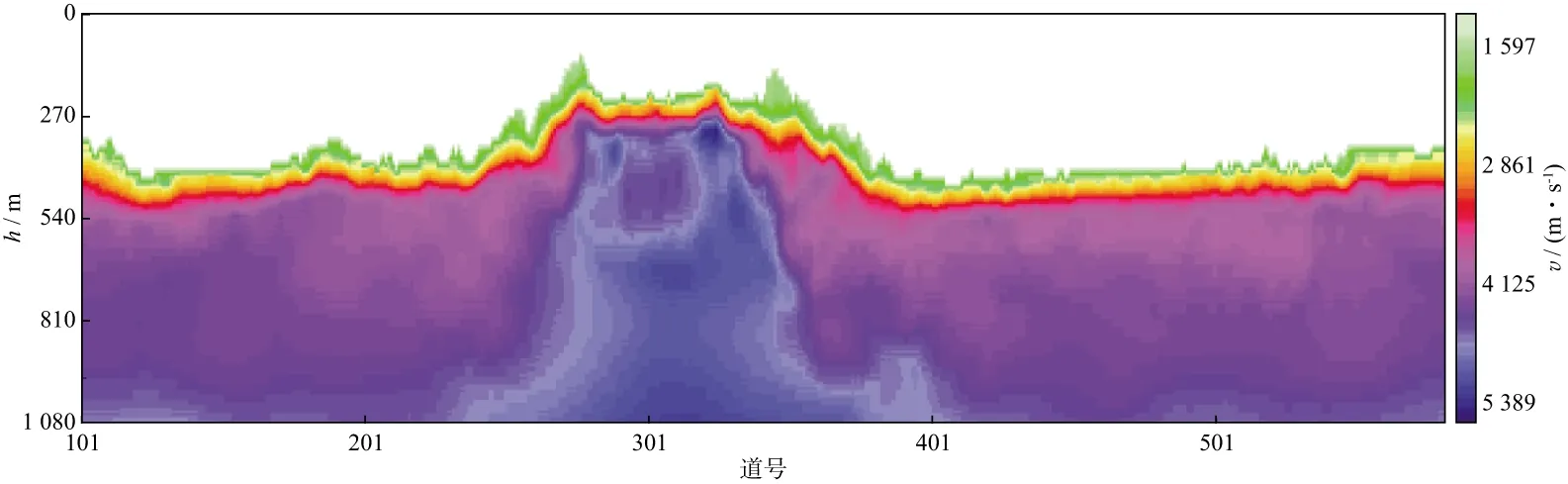
图6 背斜构造高点附近的近地表速度模型

图7 应用第1个静校正量后的叠加剖面(实例2)

图8 应用第2个静校正量后的叠加剖面(实例2)

结合应用2个静校正量的叠加剖面以及各自静校正计算方法与参数的特点,得出下面的初步判断,即第1个静校正量在控制整个工区构造形态的长波长和影响叠加效果的短波长成分方面有优势,但在控制局部区域构造形态的中波长成分方面有欠缺,中波长成分的精度不足在剩余静校正后常会使串相位更加明显;第2个静校正量在控制局部构造形态的中波长成分方面有一定的优势,但由于其短波长成分精度不够高甚至可能存在反射剩余静校正技术难以解决的较大幅值的误差,导致其叠加效果难以令人满意。

基于这样的认识,分别将第1个和第2个静校正量分解成长、中、短3个频段,利用公式(4)计算融合后的静校正量。由于第2个静校正量的中波长成分在背斜构造核心区具有优势、在工区其它区域和第1个的基本相当,可认为在整个工区均具有优势,公式(4) 中的w2(x,y)=1。经过试验并与解释人员一起分析试验结果,取波长大于10000m的静校正成分为长波长成分、波长小于1000m的静校正成分为短波长成分、其它为中波长成分。应用融合后的静校正量,并经过一次剩余静校正后得到如图9所示的结果。

图9 应用融合静校正量后的叠加剖面(实例2)

图9在保持图7整体构造形态的前提下,整个剖面的质量有明显提高。可见前述对2个静校正量特点的判断和所采取的措施正确、有效,融合静校正量的精度比第1个与第2个的都高。显然,常规的静校正融合技术无法实现这样的取长补短目标。

3 结束语

本文给出的具有地表一致性特点的静校正量分频段与分区融合技术,提供了静校正量优势互补的一种新手段,比静校正量的常规融合技术在应用效果和灵活性方面具有明显优势。要充分发挥该方法的作用,首先必须准确把握不同静校正量的叠加剖面特征,结合不同静校正量所对应的静校正方法与参数的特点,判断叠加剖面特征背后所代表的分频段静校正量的贡献,进而选择静校正量分解和融合方式;其次,在解释人员的配合下,经过参数试验获得合理的融合参数,解释人员对工区地质情况的了解,有助于给出更加合理的判断。实例给出的融合参数仅适合对应的实例,不能被认为具普遍意义。对于更复杂的具有多个静校正量和多个优势区域的情况,可以分解成多个由实例1和实例2所给出的简单情况的组合。

致谢:感谢中国石油化工股份有限公司石油物探技术研究院居兴国、王汝珍、肖盈在本技术试验阶段所做的工作和给出的建议。