绿色信贷对银行经营效率影响的动态分析——基于面板VAR模型

廖 筠，胡伟娟，杨丹丹

(天津财经大学统计学院，天津 300222)

一、引 言

绿色信贷起源于赤道原则，2007年7月12日国家环境保护总局、中国人民银行和中国银行业监督管理委员会联合提出了《关于落实环境保护政策法规防范信贷风险的意见》的绿色信贷政策，试图通过调节银行信贷达到节能减排的目的。2007年11月23日，中国银监会发布了《节能减排信贷工作指导意见》，进一步强调绿色信贷对促进节能减排的作用。2012年2月24日，中国银监会发布了《绿色信贷指引》，明确要求银行金融机构实施绿色信贷，进一步推进节能减排，消除落后生产设施[1]。绿色信贷对整个经济社会的绿色化发展起到了重要的杠杆作用，有益于生态环境的治理、保护和绿色经济的发展。一般来说，银行绿色信贷的发展通过提高经营效益、降低银行的资金风险以及提升银行的企业社会责任等方面影响银行经营效率。已有文献大多通过分析绿色信贷与银行相关变量的关系，如盈利性变量、安全性变量等，对我国银行业绿色信贷现状进行剖析，提出解决措施。许多实证研究表明，环境绩效与银行的财务绩效存在正相关关系，绿色信贷的开展有益于银行经营绩效的提升。银行的经营效率越高，银行的环境投入越多，二者相互促进。其中，绿色信贷是银行保护环境的重要市场手段，引导社会资金流向环保企业。国家鼓励并资金支持环保企业的发展，银行实施绿色信贷减轻了环境治理成本，这将使银行得到政府更多的政策支持，实现银行经营效率的提高。本文在前人的基础上综合考虑可能影响银行经营效率的各个变量，得到银行经营效率的相关数据，从绿色信贷发展和商业银行经营效率的动态分析入手，试图从定量的角度去发现商业银行实施绿色信贷的必要性，从而为探讨银行业在经济转型中如何抓住绿色信贷的机遇提供借鉴。

二、文献综述

绿色信贷是商业银行履行社会责任的必要手段。在满足利润最大化经营目标的前提下，银行会更有动力开展绿色信贷业务，因此有必要研究绿色信贷对银行经营效率的影响。

关于银行经营效率的研究方法主要有数据包络分析、动态综合评价法和主成分分析法等3种。高文娜(2018)采用2006～2015年17家银行的5个投入产出指标，分析商业银行的综合技术效率[2]。王明筠等(2015)在对银行经营效率进行测算时，分明采用了DEA模型和超效率DEA模型[3]。钟齐(2012)采取样本银行4年的财务数据，利用动态综合评价法分析商业银行经营绩效在空间和时间两个方向的发展水平和趋势[4]。朱辉(2016)考察银行评价经营效率的4个指标，利用主成分分析法得出商业银行的综合主成分值[5]。卢方元等(2012)在商业银行经营效率评价指标体系下，运用动态综合评价法得到各个银行经营效率的综合评价和排序[6]。

梳理以往关于银行经营效率的文献，动态综合评价法的运用更符合本文的要求，且该方法对变量选择和研究对象个数的选择没有硬性要求，因此本文采取动态综合评价法研究银行经营效率。

关于绿色信贷实施力度与银行经营效率之间的定量分析文章还很少，目前主要研究绿色信贷的实施是否对银行各财务指标产生影响。关于绿色信贷对银行发展是否有益，学术界存在分歧。绝大多数学者支持实施绿色信贷能提高商业银行盈利能力，如马彧菲等(2015)运用全局主成分分析法，研究发现与其他未加入赤道原则的银行相比，加入赤道原则后银行的财务状况得到很大程度的改善[7]。孙光林和李苏等(2017)运用面板数据的多元回归，研究发现绿色信贷可以有效抑制不良贷款率，也能促进商业银行盈利能力的提高，对于降低信贷风险有一定效果[8][9]。Olaf Weber(2017)研究发现中国银行的财务业绩与可持续发展表现之间存在双向因果关系，这种相互作用受到中国绿色信贷政策的影响[10]。何凌云等(2018)认为绿色信贷余额以及绿色信贷的相关内外部政策对银行竞争力有显著的积极作用[11]。孟科学等(2018)运用面板数据的多元统计回归，研究发现商业银行的绿色信贷情况与银行的高管有密切联系，股权激励制度对绿色信贷的实施有积极效应[12]。

也有一些学者认为实施绿色信贷的银行或加入赤道原则的银行短期处于规模不经济状态，长期可能可以达到规模经济，提高企业竞争力，如胡荣才等(2016)运用银行的面板数据进行多元回归估计得到结论，银行开展绿色信贷会导致其营业成本提高，盈利能力降低，但是贷款总额的增加在一定程度上会抵消绿色信贷的负作用[13]。马勇等(2017)根据问卷调查数据，运用结构方程模型，研究发现阻碍绿色信贷发展的因素是不完善的银行监管体系、绿色信贷企业较高的信贷风险、政府财政支持力度不足以及银行对企业环保信息获取渠道不畅等[14]。王晓宁等(2017)分别运用面板数据的多元回归和全局主成分分析，研究发现绿色信贷对商业银行盈利有负向作用，但是随着时间的推移，这种负向作用逐渐变小[15][16]。

还有部分学者认为商业银行是否实施绿色经济政策对经营效率没有影响，Seiferth(2004)利用结构方程模型研究了财富1000强企业中企业慈善事业的财务相关性，发现企业承担社会责任和财务绩效之间没有关系[17]。

回顾相关文献，研究绿色信贷对商业银行运营的影响时，主要运用面板数据的多元回归或者主成分分析法来探讨商业银行的盈利或者风险转移以及对商业银行声誉上的影响；变量方面，主要研究绿色信贷规模和影响银行经营效率的某一变量之间的关系，如平均资产收益率、资本充足率和不良贷款率等。本文主要着眼于银行绿色化水平对其经营效率的长期影响，运用动态综合评价模型分析得出商业银行的经营效率水平，然后利用得到的经营效率评价值与银行绿色信贷比建立面板向量自回归模型，试图去发现银行的绿色信贷对其经营效率是否有长期显著的正向作用，并就所得出的结论提出一定的政策性建议。

三、银行经营效率的综合评估

在某个时间的静态截面上，从客观、公正、合理的角度全面评价被研究对象的过程称为综合评价。在现实管理决策中，除了考虑研究对象在静态截面上的取值外，需要更多地考虑在某一段连续时间内的取值，从而得到动态综合评价值。动态综合评价法可以看作是原有综合评价法的再发展，在静态综合评价基础上加上时间因素，将应用扩展到时序立体数据表的研究上[18]。参考以往研究时序立体数据的方法，动态综合评价方法可以应用到本文银行经营效率的综合计算中。

(一)变量选取和时序立体数据表的构建

本文参考美国新骆驼银行评级制度CAMELS，主要选取银行的盈利性变量、安全性变量、流动性变量以及规模性变量进行分析。具体变量的选取如表1所示。

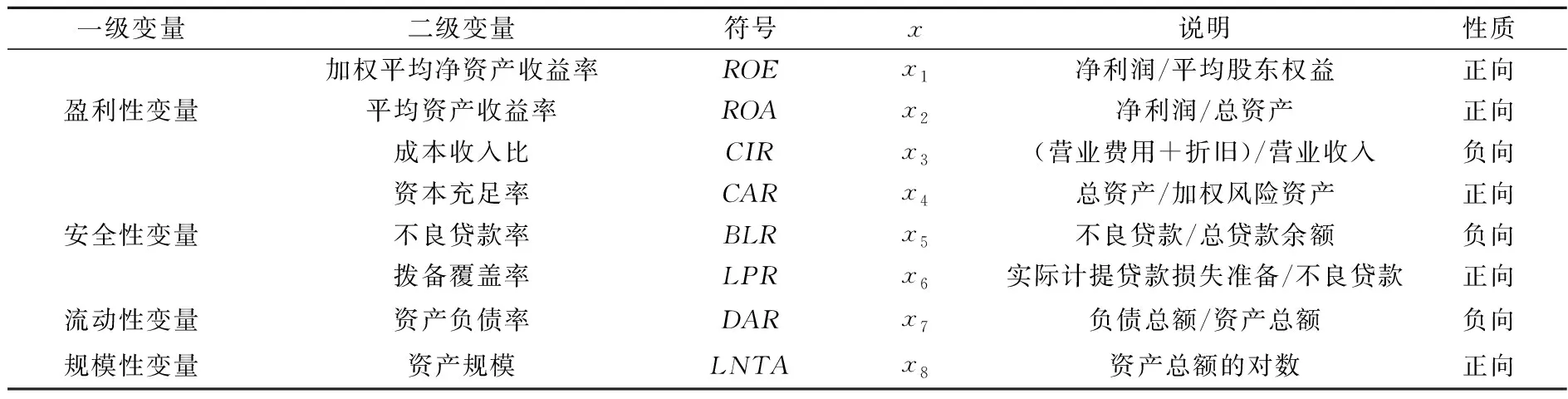
表1 商业银行经营效率的变量选取

本文选取中国工商银行、中国农业银行、中国银行、中国建设银行、交通银行、招商银行、中信银行、兴业银行、上海浦东发展银行、民生银行的年度数据进行分析。数据来源于各商业银行的年度报告、年度社会责任报告以及上海证券交易所网站。10家商业银行2008～2017年10年、8个经营效率变量数据构成了10个10×8的平面数据表，即10×10×8时序立体数据表。通过动态综合评价模型得出各银行每个年度经营效率，与年度绿色信贷比进行比较分析。

(二)模型求解

1.变量的正向化和数据标准化。考虑到变量属性的不同，首先对变量进行一致化处理，负向变量要进行正向化处理，这里采用倒数法。本文需要正向化处理的变量有成本收入比(CIR)、不良贷款率(BLR)、资产负债率(DAR)。由于各个变量的单位不一致，本文采用正态标准化对各个变量的数据进行处理。

运用R软件求出矩阵H的最大特征值：

λmax=306.35

在满足WTW=I的条件下，

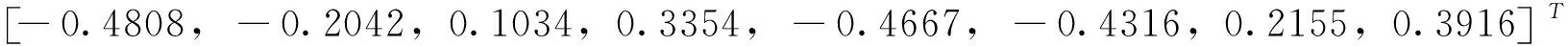
用F表示商业银行总体经营效率的评价值，则可以得到商业银行总体经营效率的评价模型：

F=-0.4808x1-0.2042x2+0.1034x3+0.3354x4-0.4667x5-0.4316x6+

0.2155x7+0.3916x8

由上式计算得出银行的经营效率评价值[注]因篇幅限制，具体数值省略，作者备索。。对10家银行年度经营效率F值直接加总，得到每年的经营效率总值，可以观察银行经营效率的整体变化趋势，如图1所示。可以发现，在2008～2011年间银行的经营效率总体处于下降趋势，2011年以后逐渐回升(图1)。从绿色信贷发展趋势来看(图2)，2008～2011年绿色信贷发展缓慢，一定程度上受到了金融危机的冲击，因此对研究二者在金融危机背景下的动态关系没有影响。

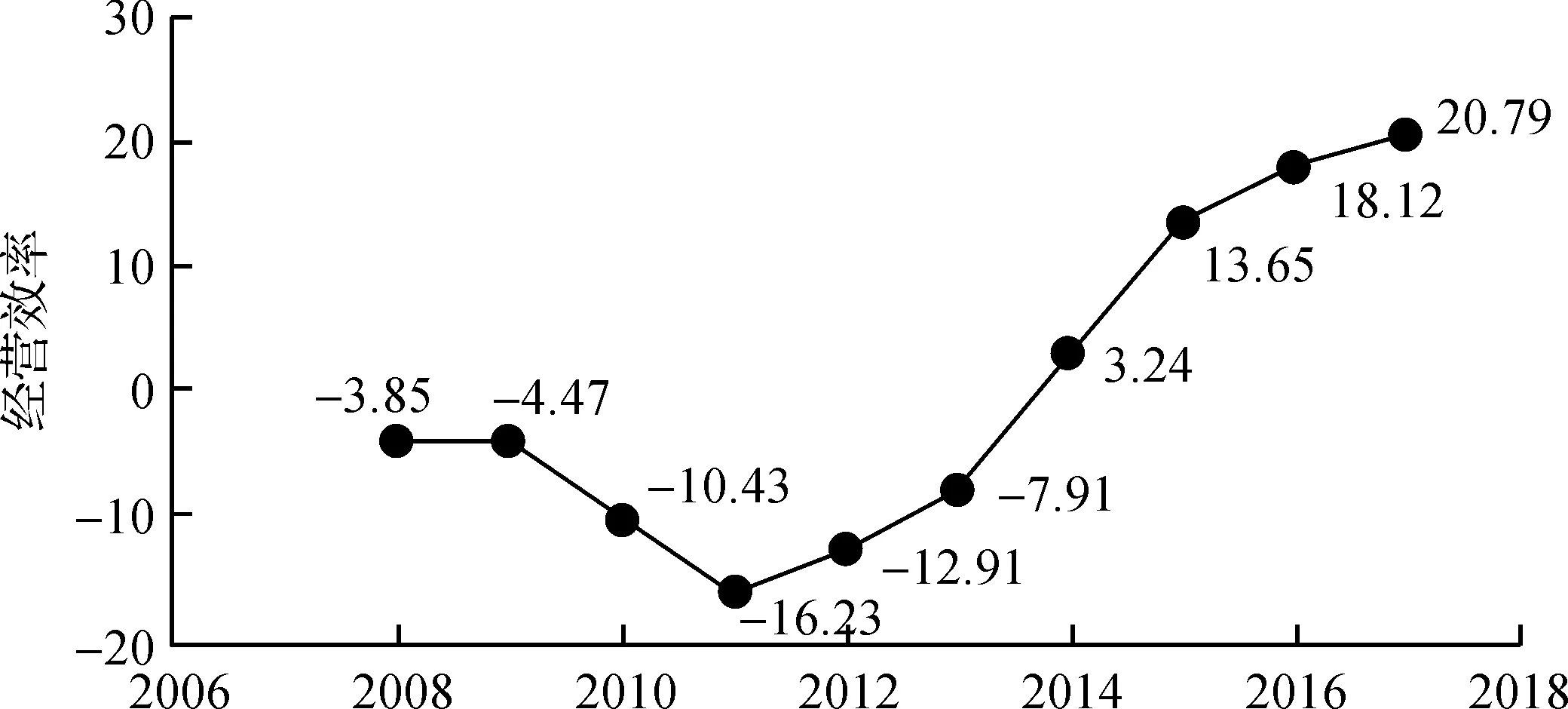
图1 10家银行经营效率走势

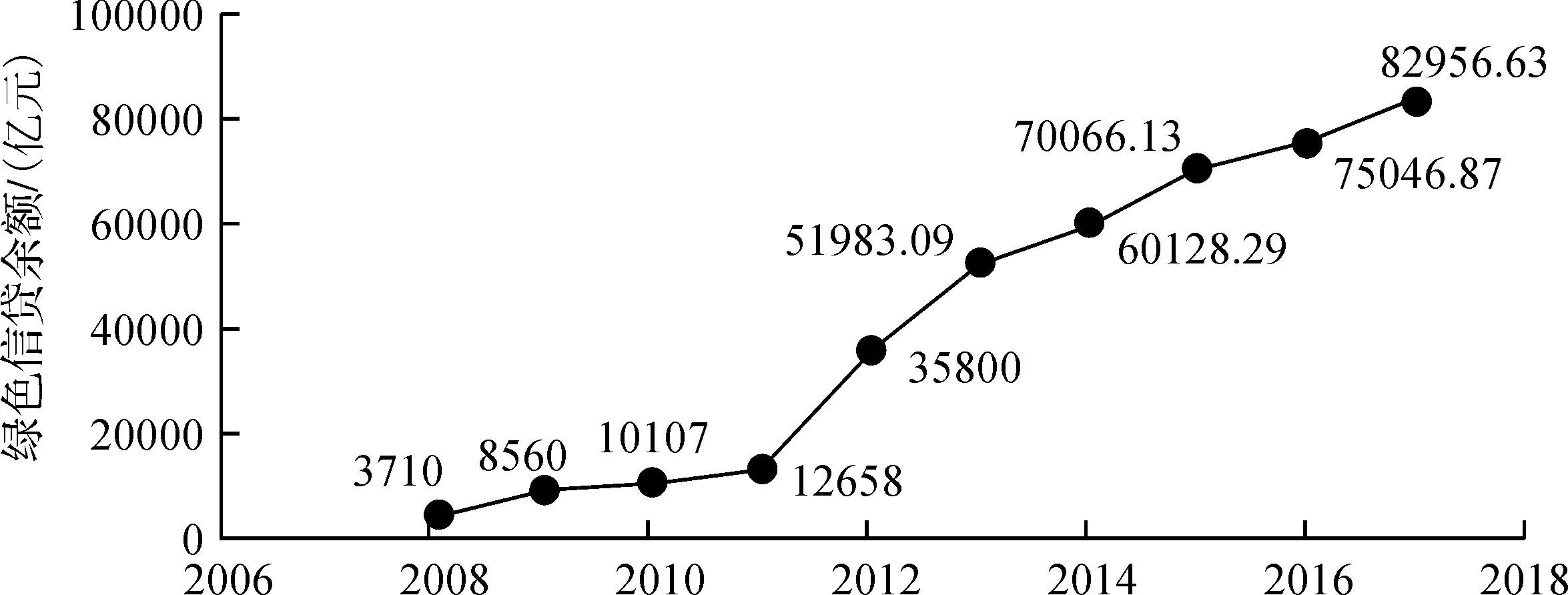
图2 2008～2017年银行业绿色信贷余额[注]数据来自2008～2017年《中国银行业社会责任报告》。

四、经营效率和绿色信贷的动态分析

(一)模型设定

面板数据向量自回归(PVAR)模型可以进行面板数据的处理，同时考虑了样本的个体效应和时间效应。本文PVAR模型的基本形式为：

其中，i=1,2,…,10表示银行，t=2008,2009,…2017表示年份，yi,t={F,glr}，p为滞后阶数，αi表示个体效应，即银行间的差异，βt表示时间效应，反映变量在时间上的特征，βp为2×2系数矩阵，εi,t是随机扰动项。

本文通过以下步骤构建PVAR模型：变量的单位根检验和协整检验；判断变量的数据是否平稳，有无长期均衡关系；模型最优滞后阶数的选择；利用面板广义矩估计(GMM)估计模型参数；计算脉冲响应函数和方差分解。

(二)实证分析

本文通过构建面板VAR模型(PVAR)分析绿色信贷对银行经营效率的影响，研究标准化后的绿色信贷比率(glr)与第三部分得到的银行经营效率(F)的关系。绿色信贷比率(glr)表示绿色信贷余额与贷款总额的比值。商业银行的社会责任报告中应明确表明绿色信贷余额，该数据易于获得并具有一定的代表性，因此本文选择绿色信贷比率作为衡量商业银行绿色信贷情况的变量。变量的描述性统计如表2所示。

表2 变量描述性统计

1.单位根和协整检验。从表3中可以看出变量的数据都是单整的，对变量F和glr进行协整检验，结果表明在5%的显著性水平下Ga、Pt和Pa都不是显著的，可以认为二者之间不存在协整关系，即不存在长期均衡关系。协整检验后可以根据是否存在协整关系决定选择面板向量自回归模型(PVAR)还是面板向量修正模型(PVEC)。当变量之间不协整时，建立面板自回归模型[20]。因此本文利用2008～2017年10家商业银行的变量数据构建PVAR模型，实证研究银行经营效率与绿色信贷之间的相互影响。

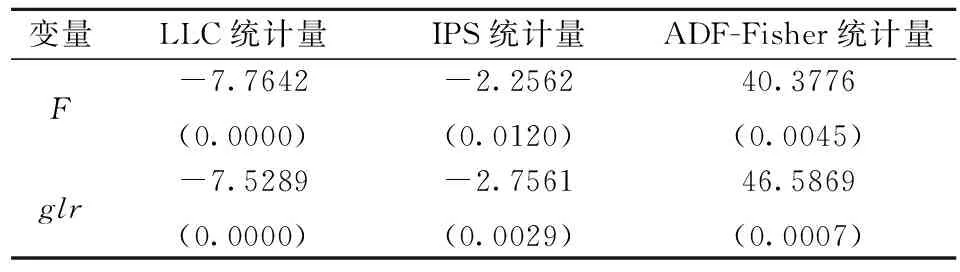
表3 面板数据单位根检验结果

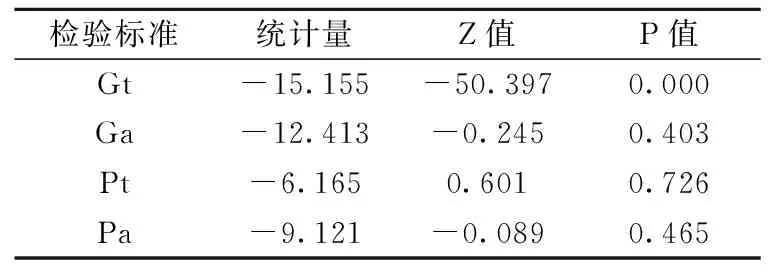
表4 经营效率-绿色信贷比协整检验结果

2.滞后阶数的选择。在Stata 14.0软件中，运行pvarsoc命令得到滞后阶数的最优选择，分析发现滞后一阶的MBIC、MAIC、MQIC值最小，所以选择滞后一阶作为最优滞后阶数研究经营效率与绿色信贷之间协整关系是合理的。

表5 经营效率-绿色信贷比PVAR滞后阶数检验

3.PVAR(1)模型估计。在模型估计之前，首先运用向前均值差分消除个体固体效应，得到h_F，h_glf。考虑到广义矩估计的稳健性，采用GMM估计模型参数，如表6所示。

表6 面板VAR模型的GMM估计结果

从表6估计结果可以看出：当h_F为被解释变量时，在95%的显著性水平下，L.h_F、L.h_glr对h_F有正向作用且显著，即滞后1期的经营效率和滞后1期的绿色信贷比能显著地促进当期银行经营效率的发展。在h_glr的回归方程中，在95%的显著性水平下，L.h_F对h_glr的作用不显著，L.h_glr对h_glr有正向作用且显著，即当期绿色信贷的实施与银行滞后1期的经营效率无关，上一期的绿色信贷规模大小会显著地影响本期的绿色信贷投入。

4.脉冲响应函数。通过观察PVAR的回归结果可以直观地了解到变量间的关系，但是变量之间的长期动态关系还需要通过观察脉冲响应函数来分析。图3为经营效率和绿色信贷两个变量的脉冲响应图。

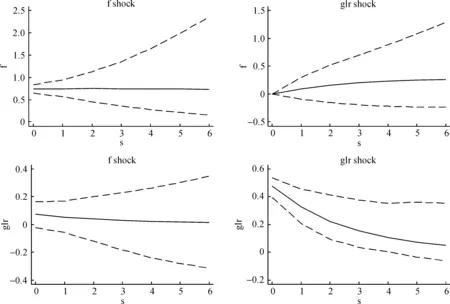
图3 经营效率-绿色信贷比脉冲响应函数

从图3可以看出：在本期给F一个标准差冲击后，对自身的影响在第一期内是正向作用，并且这种促进作用逐渐降低并趋于平稳；F的标准差冲击在期初对glr有明显的正向作用，2期以后对glr的影响逐渐减弱，这说明绿色信贷与银行自身发展的发展密切相关。glr的标准差冲击对F的脉冲值在逐渐加强；在本期给glr一个标准差冲击后，对自身的影响在第一期内是较为明显的正向作用，并且这种促进作用逐渐降低并趋于平稳。

5.方差分解。本文采用方差分解法分析经营效率和绿色信贷对其波动的相对贡献率，表7给出了具体的方差分解结果，包括第10期、20期、30期的预测方差分解。

从方差分解的结果可以看出：绿色信贷比对自身冲击较大，在第10期，对自身方差的贡献率达到97.20%，在第30期稍微下降至96.90%。绿色信贷比对银行经营效率的变动解释能力较强，在第30期达到11.34%，说明在考虑绿色信贷时，商业银行经营效率变动的11.34%可由绿色信贷解释。银行经营效率对其自身的影响最大，在第30期为88.66%。经营效率对绿色信贷比的影响比较小，但一直处于上升趋势，在第30期为3.10%，这表明银行经营效率的高低可能会影响绿色信贷的发展。

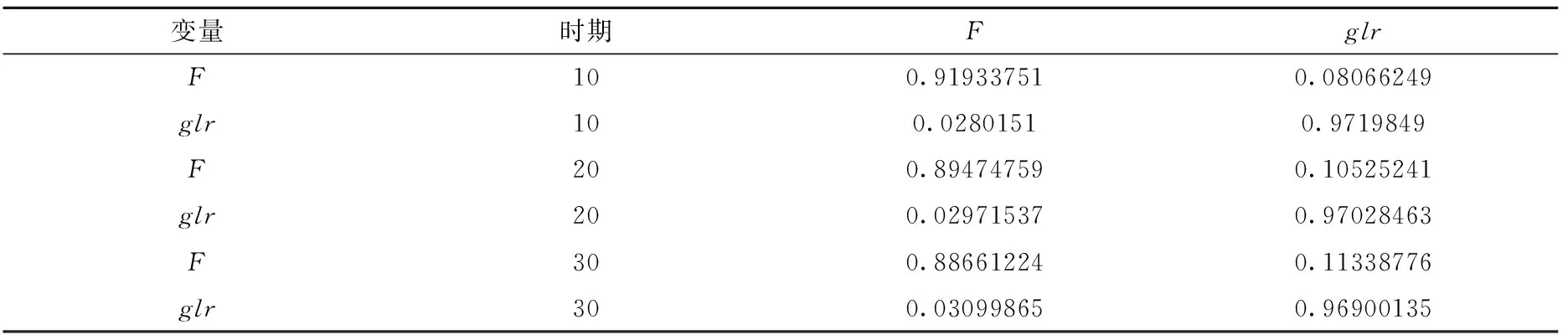
表7 PVAR模型的方差分解结果

五、结论和建议

本文分析了绿色信贷发展与银行经营效率之间的动态关系，利用2008～2017年10家银行4个方面(盈利性、安全性、流动性、规模性)8个变量数据进行综合评价分析，得到商业银行的经营效率评价值，然后利用得到的经营效率评价值数据与标准化的绿色信贷比率数据建立面板向量自回归模型，实证分析绿色信贷发展与银行经营效率之间的影响和相互关系。广义矩估计结果表明：在95%的显著性水平下，绿色信贷对商业银行的经营效率有正向影响；进一步，通过分析脉冲响应图可以看出绿色信贷的波动对银行经营效率具有持久的正向冲击；在预测方差分解中，绿色信贷对银行经营效率的方差贡献率达到11.34%，这表明银行经营效率的波动在一定程度上是由绿色信贷发展引起的。

绿色信贷是调动企业及社会各界力量参与环保事业的一个杠杆。激发银行实施绿色信贷的积极性，可以促进整个社会企业向绿色化经济体系发展。基于此，本文提出以下建议：第一，强化绿色信贷意识，将绿色信贷融入企业信贷文化建设，制定一套有效的银行长期发展规划。积极创新绿色信贷产品，建立严格的信贷审核标准，将环境风险管理与信贷审批流程紧密结合。第二，政府应制定明确的绿色信贷标准，明确界定“两高一低”和绿色信贷的范围标准和统计口径并公布，接受社会公众的监督。第三，建立有效的激励机制。政府应当对银行采取适当的激励政策，对切实实施绿色信贷且成果显著的银行实行奖励，如减免税收、财政贴息等，推动银行更加自觉开展绿色信贷。第四，加快推进环境信息强制披露政策，将环境标准与社会责任融入到银行整体信贷及贷款项目评估的流程中，减少银行绿色信贷的成本。