应用正交试验分析电示功图影响因子显著性

，，， ，

(1.中联煤层气有限责任公司 晋城分公司，山西 晋城 048000；2.中国石油大学 机电工程学院，山东 青岛 266580)

示功图是煤层气井生产管理与评价的重要参数，示功图的准确获取是分析井下工况的必要条件。通过电参数获取示功图，对排采系统工作参数影响因子进行分析，可以满足煤层气排采数据的不停产标定的要求，实现排采数据的实时、长期、连续监测。

影响电示功图的因素众多，例如系统转动惯量、系统效率、电机特性等。由电参数反演计算示功图过程中，难以定量测试和表征上述因素，并且各个变量的影响程度都为未知，故需对示功图测试精度影响因子进行分析，而基于电示功图的特征值数值模拟是一种行之有效的方法[1-5]。

本文从抽水机实际模型出发，建立电参数与载荷间的输入输出系统模型，提出一种基于优化算法，利用电参数间接获得示功图的方法。分析得出系统参数对测量精度影响的显著性因子，利用正交分析法判断各个影响因素对电示功图特征值影响的大小顺序，及各个影响因素与特征值的相互关系。实现参数的自修正和调整，提高测试的精度，为实现排采设备运行参数连续、可靠测试打下理论基础，并通过现场测试进行验证。

1 电示功图求解

1.1 理论建模分析

为了求解抽水机的实际运动规律，建立抽水机的等效动力学模型。取曲柄为等效构件，如图1所示。

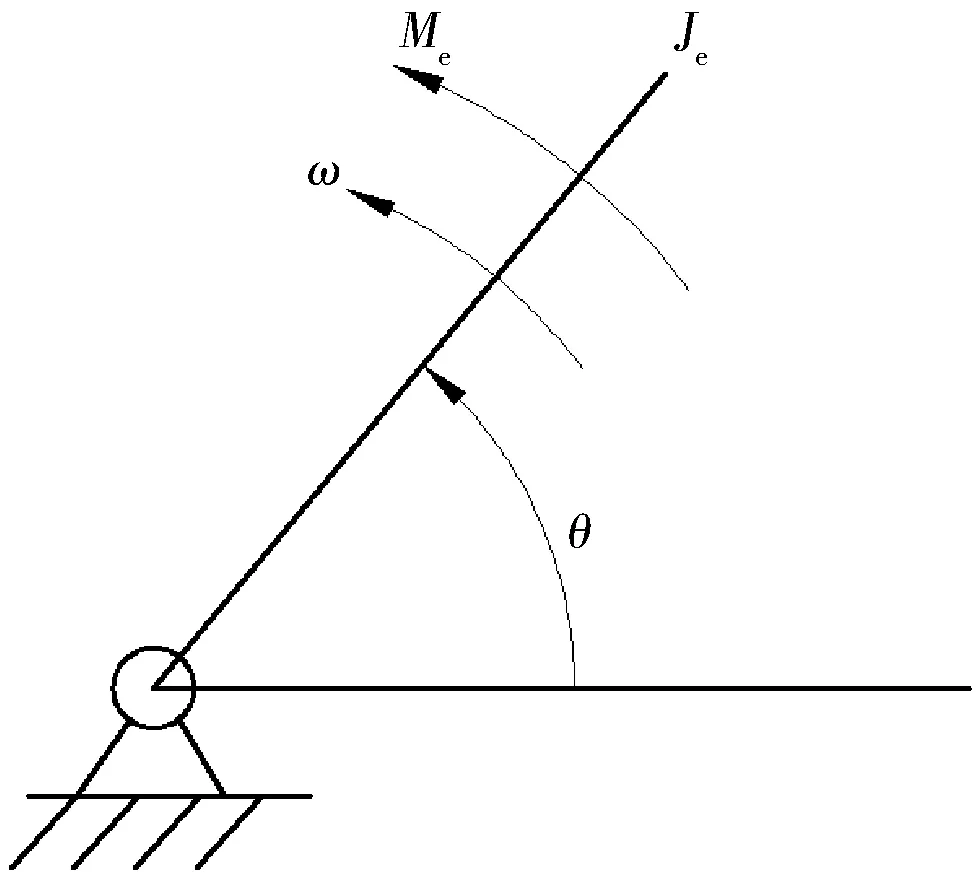
图1 抽水机系统等效构件

1) 运动微分方程建立。

根据系统动能定理，可得系统等效动力学方程为：

(1)

式中：Je为抽水机系统等效到曲柄轴处的等效转动惯量，kg·m2；ω为等效构件曲柄角速度，rad/s；Me为抽水机系统等效到曲柄处的等效力矩，N·m；θ为等效构件曲柄转角，rad。

2) 等效转动惯量计算。

(2)

式中：J1为曲柄、减速箱和电动机等效到曲柄上的等效转动惯量，kg·m2；J3为游梁系统绕游梁回转中心的转动惯量，kg·m2；ω3为游梁角速度，rad/s；ω1为曲柄角速度，rad/s。

3) 系统等效力矩计算。

为了计算等效力矩Me，需要计算抽水机系统的等效驱动力拒Md与等效阻力矩Mr。综合带入系统等效表达式中，可得系统等效力矩的表达式[6]：

(3)

式中：Me为等效力矩，N·m；i为电机到曲柄的传动比；Md为电机驱动力矩，N·m；Mr1为曲柄系统阻力矩，N·m；Mr3为游梁系统阻力矩，N·m。

4) 等效动力学模型的求解。

由于Je和Me用解析式求解困难，用迭代法对方程进行求解[7]。将上式结合，用Δθ代替dθ，由此可解出ωi+1的表达式：

(4)

根据抽水机工况参数，给出等效构件曲柄的初值ω0，就可以求出曲柄任意时刻的角速度ωi。

1.2 Powell优化算法计算示功图

电参数与载荷间具备输入输出关系，通过建立电参数与示功图的目标函数，采用Powell算法反演计算悬点示功图。Powell算法是一种局部多参数最优化计算，相对于全局优化算法有较快的收敛速度。在每一次迭代中，都要从初始点进行一维搜索，搜索方向是Powell算法中的另一个重要参数，用一个多方向集C表示。

Powell算法具体的优化过程分为若干次迭代，每次迭代都由N+1次一维搜索组成，其中N是搜索空间的维度。算法每次迭代过程的步骤是，从初始点开始，依次沿方向集的N个方向进行一维搜索，得到一个最优值及最优值对应的点。然后沿该点和初始点的连线的方向进行搜索，求得本次迭代的最佳值及其对应的点，然后把连线的方向替换为前N个方向效果不好的方向，形成新的方向集，进行下一次迭代[8]。

具体构造过程：

1) 将方向集Ci初始化：Ci=e(i=1,2,…,N，e为坐标轴的单位向量)。

2) 记录初始点位置P0。

3) 从Pi出发，以此沿方向集的各个方向寻找该方向归一化信息的极大值点，记该点为Pi+1，以该点为新的出发点，进行下一次迭代搜索。

4) 重复步骤3，直到新点和前一点之间的距离||Pi+1-Pi||<ε(ε为设定精度值)，该值为算法的解。

功率测试仪主要用来测量电机的功率值，可实现电参数连续、实时测量。实测电机输入功率，读取测试数据，取一完整周期功率数据，对测试数据进行平滑处理。通过动力学方程计算得到的曲柄真实角速度，根据曲柄一周的时间，得到曲柄角速度与时间的关系，进而将一个周期测试功率与时间的关系转化为功率与角度的关系，便于与计算功率作对比。

根据建立的等效动力学模型，计算等效曲柄力矩M和曲柄真实角速度ω，则可得曲柄功率P。

P=Meωη

(5)

式中：η为系统总效率；P为计算曲柄功率，W。

建立测试功率与输出功率误差最小为目标函数。采用Powell优化算法，使目标函数最小，优化计算得到示功图。

(6)

式中：F为目标函数，Pt为测试功率，W。

Powell算法是以共轭方向为基础寻求最优解的算法[9]。给定初始载荷和误差，采用Powell优化算法进行循环迭代计算，直至满足计算误差，计算得到示功图。

1.3 算例分析

中联某抽水机的型号为CYJ12-4.2-73HB，减速箱型号为JS-1000，电动机型号为Y280-S,冲程为4.2 m，冲次1.9 min-1，泵径ø56 mm，下泵深度为1 256 m。

测得煤层气井驱动电机瞬时功率的条件下，运用等效动力学模型逆分析相关理论，编写MATLAB程序，求解悬点载荷(示功图)。编制Powell算法，以计算功率与实测功率误差最小为目标函数，得到计算结果迭代过程如图2～3所示。

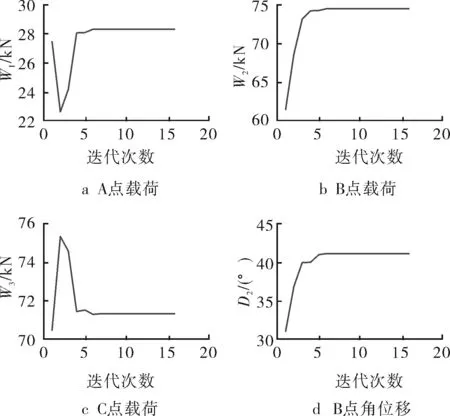
图2 悬点载荷迭代过程

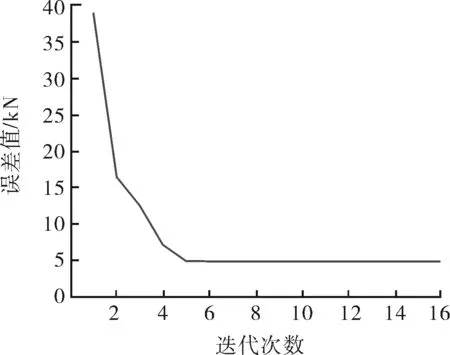
图3 误差迭代过程

经过Powell优化计算得到悬点载荷，以此为基础，通过抽水机系统动力学模型，计算曲柄真实角速度，由输出转矩得到曲柄瞬时功率，将计算功率与实测功率曲线进行直观对比。得到计算结果曲线，如图4所示。

图4 示功图对比

2 正交试验分析

显著性因素分析是在确定的目标函数影响因子范围与特征值条件下，采用控制变量法，通过改变目标函数影响因子的数值，将正交分析法用于判别电示功图影响因素的显著性。设计正交矩阵，分析电示功图影响因素的水平组合。用方差分析法对影响因子进行量化评价。本文对计算所得电示功图影响因子设计正交试验，进行显著性分析。

另外，还应当投入专项资金，用来支持高校教育资源共享活动。在中观层面上，地方政府要不断加强对区域共享平台的建设和完善，对有困难的高校采取一定的优惠政策，在经济上提供支持。为使地方高校有更大的社会影响力，支持高校采用共享政策，积极引进教育资源。在宏观层面上，国家和地方政府需要继续加大对现有共享资源和平台的投入力度，保证高等学校仪器设备和资源共享系统、中国高等教育文献保障体系等正常且高效率地运行。同时，在网络共享技术方面进行创新发展，为新的共享平台的开发和建设加大投入。

2.1 影响因子的计算

系统效率的计算包括电机、皮带和减速箱的效率。我国煤层气井的抽水机采用同步永磁电动机，效率变化平稳，采用额定效率0.95。减速箱承受较大的转矩和转速，稳定效率为0.92。抽水机皮带的正常工作效率有3种状态[10]，如图5。

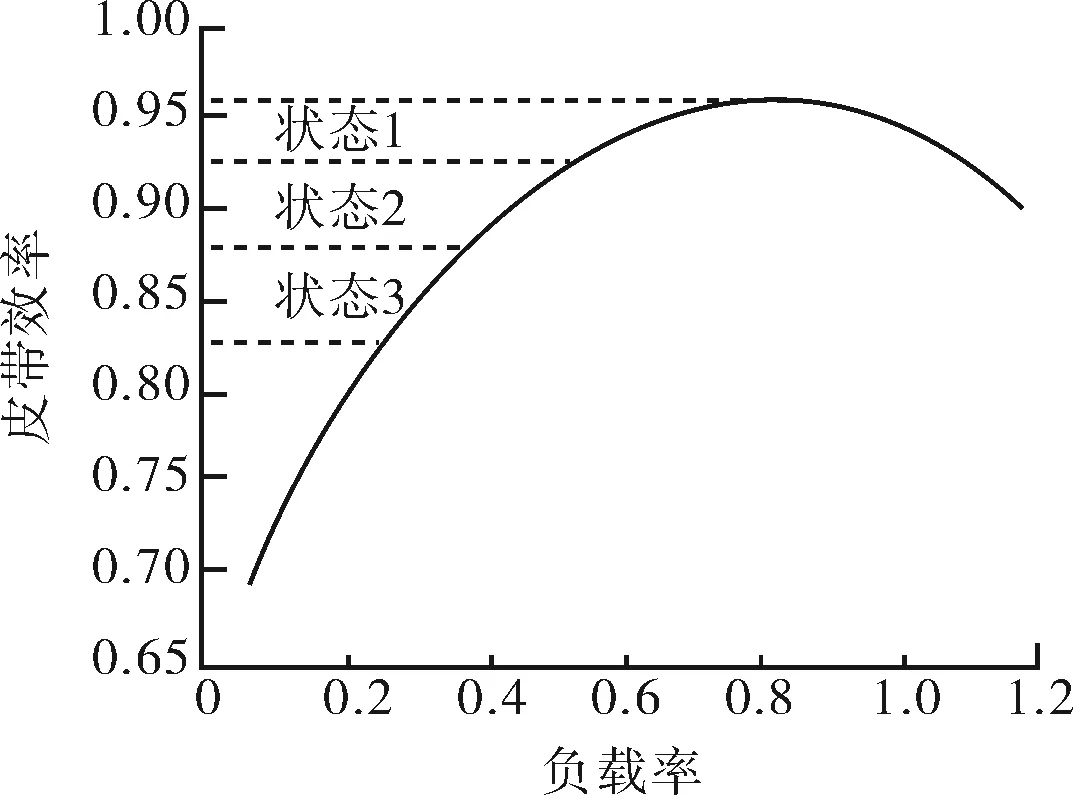
图5 皮带效率的三个状态

2.2 正交分析法

电示功图影响因素显著性分析，就是定量分析影响示功图最大最小值、面积、斜率和各因素的相关性，即分析各个影响因素的变化对电示功图的影响程度。本文采用正交分析法研究电示功图最大最小值、面积、斜率对各个影响因素的敏感性，进而区分影响电示功图的主要因素和次要因素。设计正交矩阵来分析电示功图影响因素，用方差分析法对电示功图影响因素的显著性进行量化评价[11]。

正交分析法是一种统计方法，利用已有的正交表安排多因素实验，再对结果进行统计分析的科学方法。利用正交分析法可以判断各个影响因素对所考察指标影响的大小顺序以及各个影响因素与考察指标的相互关系，采用方差分析法分析实验结果，用各个影响因素的变差平方和与误差平方和相比，作方差齐性检验，从而判断实验结果对各影响因素的敏感性[12]。

用正交表设计试验计算方案，对试验计算结果进行方差齐性检验，计算矫正数为

C=T2/n

(7)

试验总偏差平方和为

SST=∑x2-C

(8)

试验各影响因素偏差平方和及误差平方和为

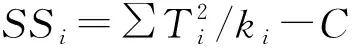
(9)

总偏差平方和自由度、单个影响因素偏差平方和自由度、误差平方和自由度分别为

dfT=n-1

dfi=ki-1

(10)

方差齐性检验统计量Fj为[12]

Fi=(SSi/dfi)/(SSe/dfe)=(SSi/SSe)

(11)

式中：T为试验指标之和，kN·m；n表示试验数，无量纲；x为各试验指标值，kN·m；SST为所有因素的偏差平方和总，(kN·m)2；SSe为误差平方和，(kN·m)2；SSi为影响因素的偏差平方和，(kN·m)2；Ti为各因素同一水平试验指标之和，kN·m；ki为各因素同一水平数，无量纲；dfT为总自由度，无量纲；dfi为各因素自由度，无量纲；dfe为误差自由度，无量纲；Fi为构造的方差齐性检验统计量，无量纲。

2.3 正交试验结果与分析

对上述得到的电示功图进行影响因子显著性分析。采用控制变量法，分别改变系统效率、电机特性和转动惯量的值，计算得到不同影响因子的电示功图对比曲线，如图6～8所示。

图6 不同效率状态示功图对比

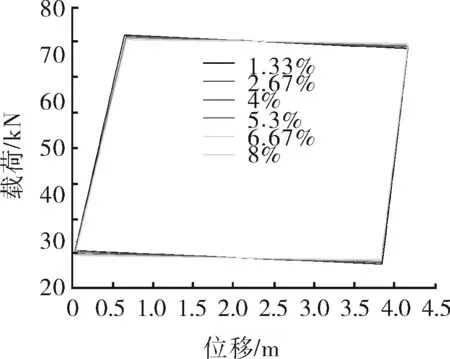
图7 不同电机特性示功图对比

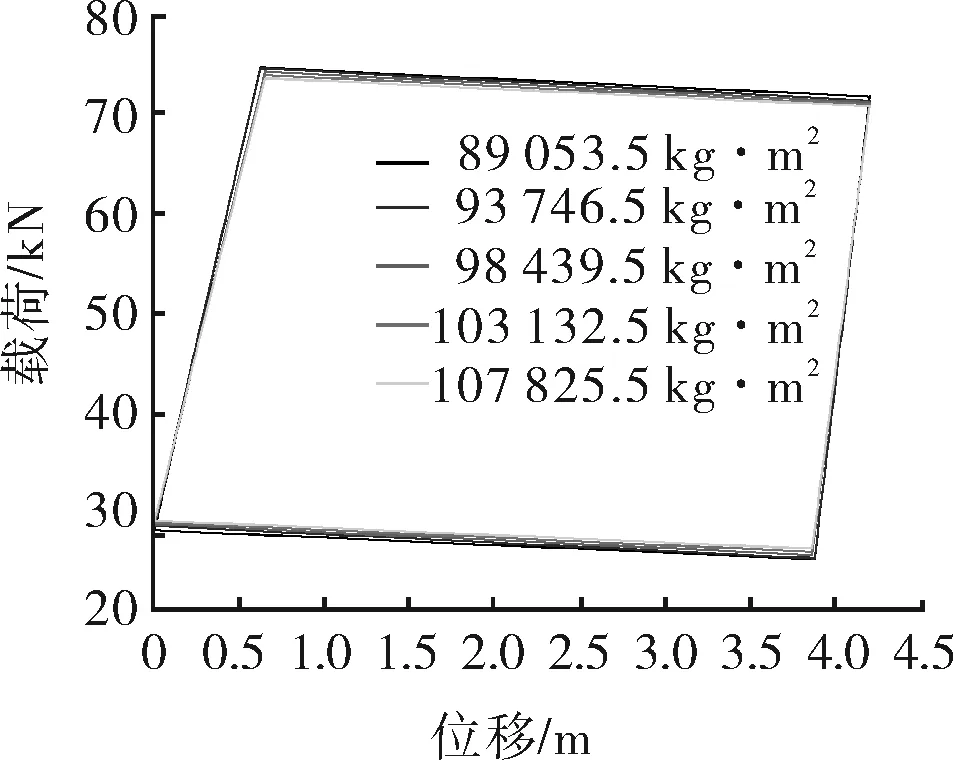
图8 不同转动惯量示功图对比

设置三水平三因素正交试验，选取每组影响因子的3个典型数值进行显著性分析，如表1所示。

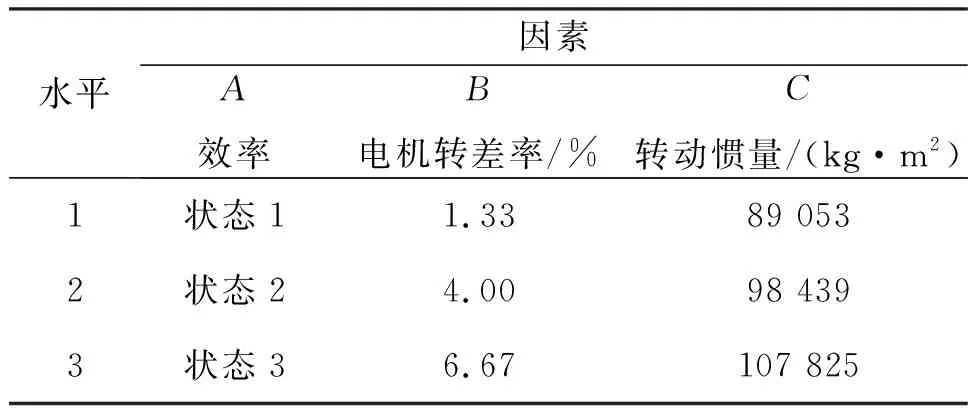
表1 因素水平

根据正交分析法的设计原则，选取正交表为L9(33)正交试验，为全面分析电示功图对各个影响因素的敏感程度，设计9组计算、试验，对电示功图最大值、最小值、面积和斜率等特征值为计算结果进行方差齐性检验，如表2所示。

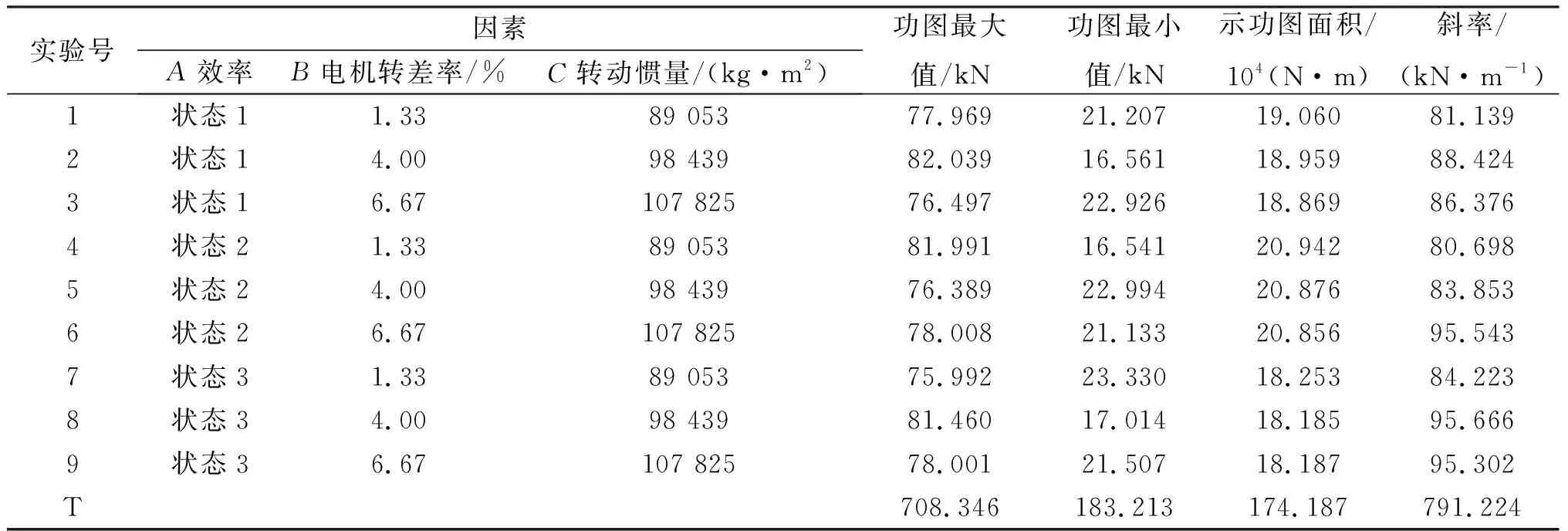
表2 实验安排及计算结果

计算上述试验的电示功图如图9所示。

对设计的正交试验电示功图最大值和最小值计算结果进行统计变量分析，如表3～4所示。其中，Ki表示正交试验中任意列上水平号为i时所对应的试验结果之和，ki表示Ki对应的平均值。

图9 计算示功图对比

表3 不同影响因子电示功图最大值统计变量计算结果

表4 不同影响因子电示功图最小值统计变量计算结果

对设计的正交试验进行方差分析，计算试验电示功图最大值和最小值总变异及误差变异如表5～6所示。

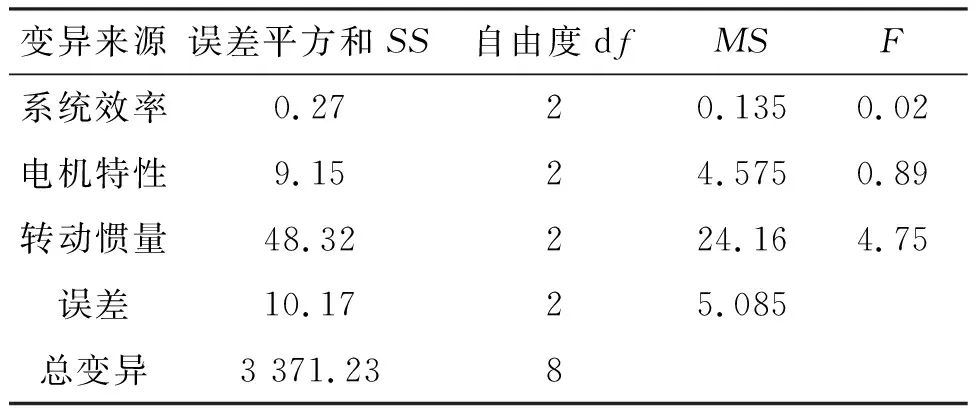
表5 电示功图最大值方差分析数据

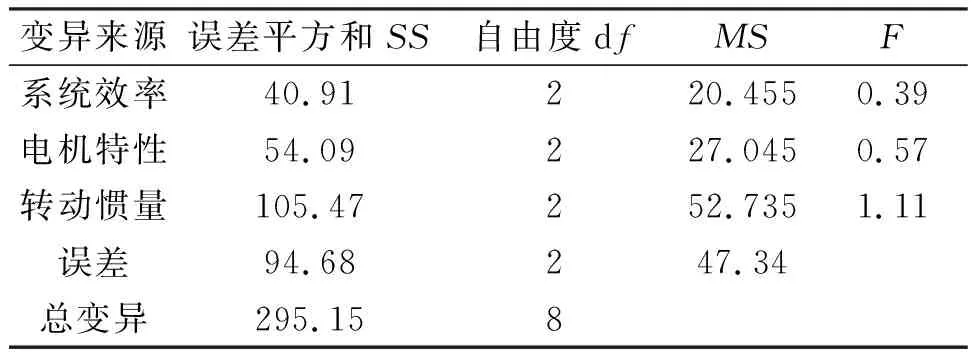
表6 电示功图最小值方差分析数据

对设计的正交试验电示功图面积和斜率计算结果进行统计变量分析，如表7～8所示。

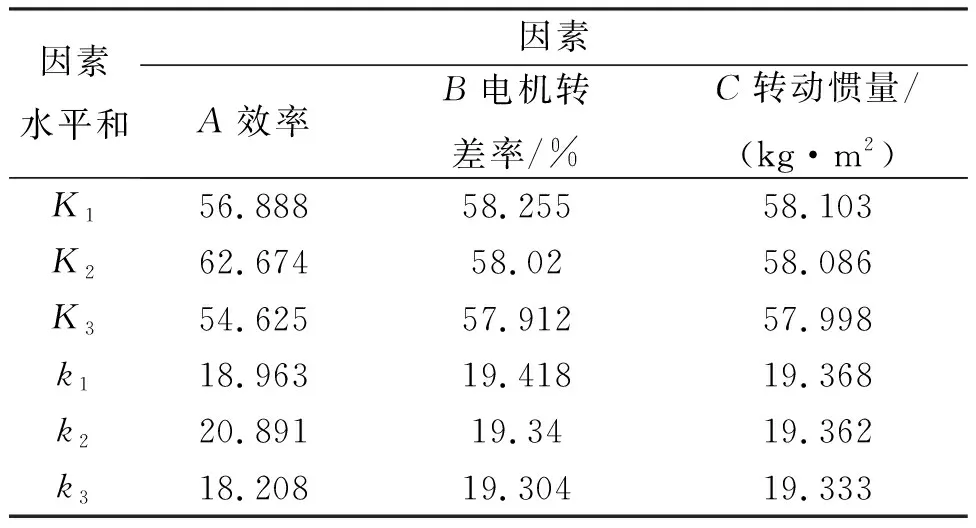
表7 不同影响因子电示功图面积统计变量计算结果

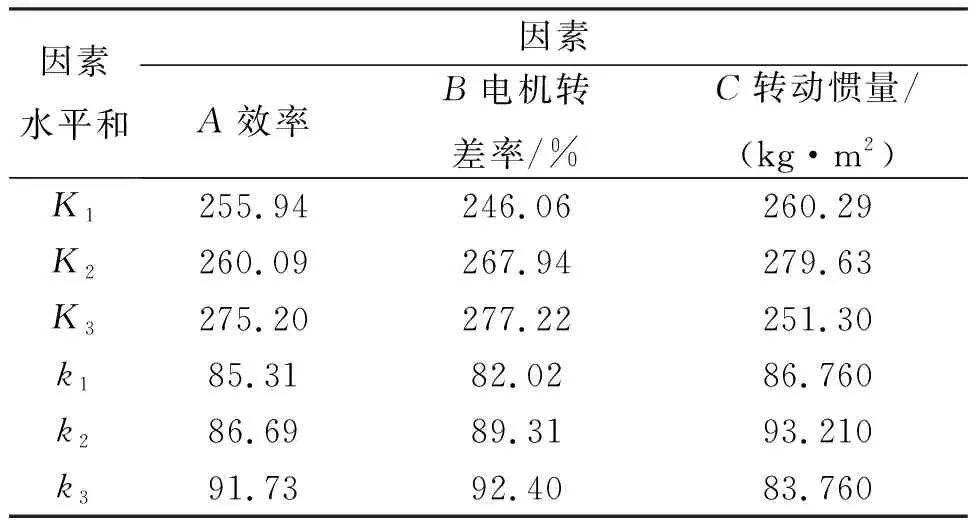
表8 不同影响因子电示功图斜率统计变量计算结果

对设计的正交试验进行方差分析，计算电示功图面积总变异及误差变异，如表9所示。

表9 电示功图面积方差分析表

对设计的正交试验进行方差分析，计算电示功图斜率总变异及误差变异，如表10所示。

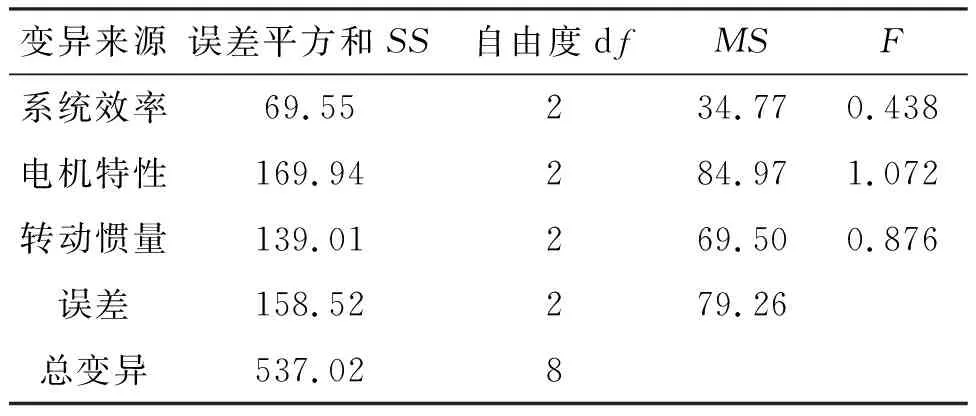
表10 电示功图斜率方差分析数据

选取水平α为0.01，0.05，0.10，查方差齐性检验分布表可得：F0.99(4,4)=16，F0.95(4,4)=6.39，F0.90(4,4)=4.11，若Fi≥16.00，表示示功图特征值对影响因素i高度敏感；若6.39≤Fi<16.00，表示示功图特征值对影响因素i较敏感；若Fi<4.11，表示示功图特征值对影响因素i不敏感。F检验结果表明，系统转动惯量对电示功图最大最小值影响最为显著，系统效率对电示功图面积影响最为显著，电机特性对电示功图的斜率影响最为显著。

将不同电机特性与不同转动惯量影响的特征值计算结果进行综合，如图10～11所示，根据计算结果可得示功图斜率与转差率关系式和最大值、最小值与转动惯量关系式。

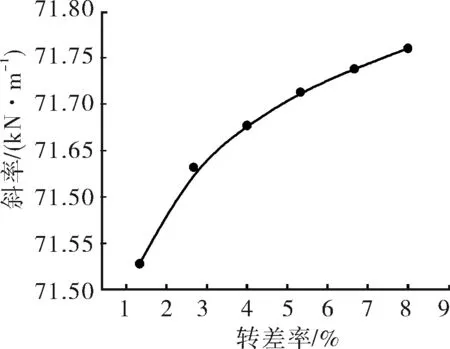
图10 示功图斜率与转差率

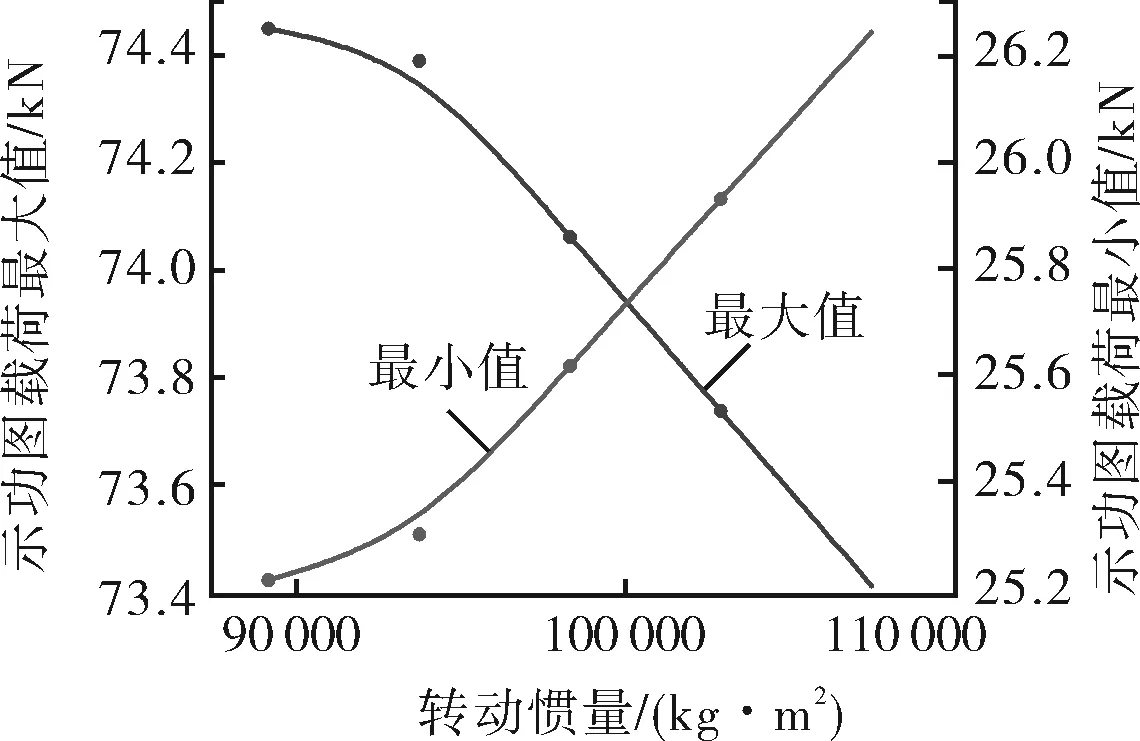
图11 示功图最大、最小值与转动惯量

斜率：k=0.127 8ln(100S)+71.498

(12)

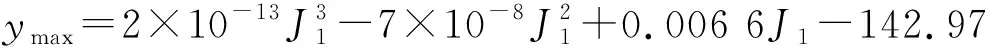
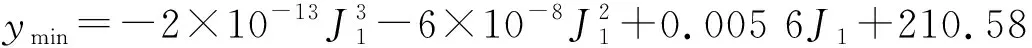
(13)

3 结论

1) 为了分析影响煤层气抽水机的电示功图测试精度的因素显著性，建立了抽水机的动力学模型，通过Powell算法得到最优示功图。采用控制变量法改变目标函数影响因子数值，得到特征值变化。并结合正交分析法和方差齐性检验，确定特征值影响因子的显著性。

2) 将正交分析法应用于电示功图的各个影响因子的显著性分析，能有效地区分影响电示功图的主要因素和次要因素。各影响因素对电示功图影响显著性不同，影响电示功图最大值和最小值由强到弱依次为：转动惯量、电机特性、系统效率。影响电示功图面积由强到弱依次为：系统效率、电机特性、转动惯量。影响电示功图斜率由强到弱依次为：电机特性、转动惯量、系统效率。根据影响因子显著程度，得到影响因子与电示功图特征值的定量关系。

3) 通过建立系统参数对测量精度影响的显著性因子，实现参数的自修正和调整，提高测试的精度，对实现煤层气排采设备的自动化控制具有重要意义。