基于深度动态学习神经网络和辐射传输模型地表温度反演算法研究*
2019-01-29毛克彪韩秀珍唐世浩袁紫晋高春雨
毛克彪,杨 军,韩秀珍,唐世浩,袁紫晋,高春雨
(1. 中国农业科学院农业资源与农业区划研究所,北京100081;2. 湖南农业大学资源环境学院,长沙410128;3. 国家气象卫星中心,北京100081)
0 引言
温度是表征地球各圈层(岩石圈、水圈、大气圈和生物圈)之间能量传输的重要物理量,地面温度(包括地表和近地表)是研究地表和大气之间物质和能量交换、全球海洋环流、气候变化异常等方面不可或缺的重要参数,涉及众多基础学科和重大应用领域。运用卫星遥感技术快速准确地获取大面积、长时间序列的地表温度,是顺应当前科学技术发展趋势,是应对多种自然灾害等诸多问题迫切需要开展的研究课题,其研究成果既具有重大的科学意义,同时也具有重要的社会经济价值。最近几十年,大尺度上环境研究和管理活动对温度信息的需求已经使得利用遥感手段反演地表温度和发射率的技术有了很大进步。MODIS是对地观测卫星(EOS)上的一个传感器,它拥有36波段。能够覆盖全球、辐射分辨率非常高、动态范围以及精确校正等特点使得MODIS传感器在海面温度、陆地表面温度和大气参数反演方面具有非常大的潜力。
从多个热红外波段的测量中同时反演地表温度和发射率非常困难,因为N个波段至少拥有N+1个未知数(N个波段的发射率和地表温度),这是一个非常典型的病态反演问题。如果不利用任何先验知识,几乎不可能同时从多个热红外数据中反演地表温度和发射率。许多劈窗算法已经被开发来从NOAA/AVHRR和MODIS数据中反演海面温度和地表温度,这些反演方法主要是利用相邻热红外波段对水汽的敏感性不一样来校正大气水汽的影响[1-14]。这些算法形式基本上相同,主要差别在于关键参数的获取及计算。虽然大多数的算法精度都很高,但它们仍然需要做一些假定并利用发射率和大气状态(特别是大气水汽含量)作为已知的先验知识。许多研究人员[15-21]在地表温度和发射率反演方面做了许多工作,特别是Li和Becker利用TISI(Temperature Independent Spectral Index)技术和白天/晚上的影像数据反演地表温度和发射率[22],这个反演方法需要大气剖面信息。Wan和Li提出了一个多波段算法从EOS/MODIS传感器中同时反演地表温度和发射率[23],这个方法受地面的光学性质和大气状态的影响。这两个方法都假定了白天和晚上同一地点的发射率不变,由于云等条件的影响,使得产品的分辨率降低为5 km。毛克彪等提出利用辐射传输方程与人工智能相结合的方法反演地表温度,该方法的优点是只需要使用同一景热红外遥感数据就可以反演地表温度和发射率,克服了白天/晚上算法的缺陷[24-29]。
地球上各种成分不是独立的,而是彼此相互联系的。毛克彪等首次系统地阐述了利用地球物理参数之间的关系构造额外方程消除反演病态问题,并用人工智能神经网络基于辐射传输模型等方法进行优化计算[29]。但毛克彪等只对MODIS白天的热红外波段和水汽波段反演做了评价分析[29],没有对适合于白天和晚上的热红外波段做模拟分析,也没有对近红外波段与热红外波段联合反演晚上的温度做分析。该研究拟利用MODTRAN4和深度动态学习神经网络分别对适合于白天、白天/晚上和晚上的热红外和近红外反演地表温度做单独模拟评价分析,从而为风云系列卫星和高分数据地表温度反演提供参考模式。
1 地表温度反演基本原理
地表温度反演是基于辐射传输方程,利用地表热辐射从地表途经大气达到传感器的过程建立热平衡方程。通常讲,地表不是黑体,在计算地表热辐射时需要考虑地表发射率,同时热辐射传输过程中大气对传感器接收到的能量也有贡献。考虑到这些因素,通用的辐射传输方程可以描述成方程(1)。

式(1)中,Ts是地表温度,Ti是通道i的星上亮度温度,τi(θ)是通道i在θ角时的透过率,εi(θ)是通道i在θ角时的地表发射率。Bi(Ts)是地表辐射强度,和分别是大气向上和向下的辐射强度。和可分别用如下公示表示:
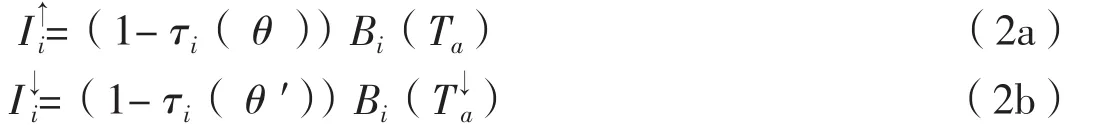
Ta是向上的大气平均作用温度,是向下的大气平均作用温度。将和代入式(1)可得:
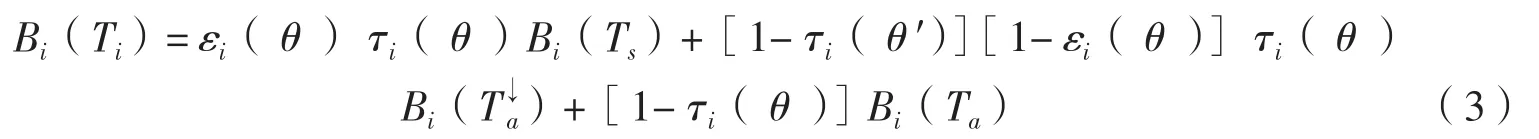
Qin et al.[11]、Mao et al.[13]对等式(3)做了一些分析和合理的简化,得出用Ta代替对反演方程不会有太大的影响,所以式(3)可以描述成式(4)。
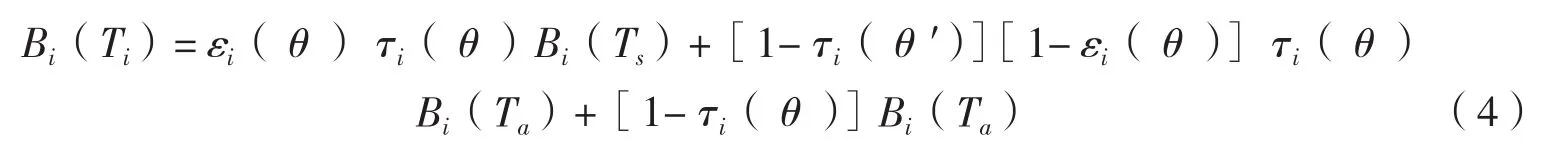
每个方程中,有3个未知数(1个波段的发射率、地表温度和大气平均作用温度),这是一个典型的病态问题。为了反演地表温度和发射率,需构造其它的方程和限制条件。地球物理参数彼此之间不是独立的,而是相互联系的。在以往的算法中,没有充分利用地球物理参数之间的关系。毛克彪等[25-29]利用波普曲线对不同波段的发射率之间的关系,大气水汽含量与透过率之间的关系,近地表空气温度和大气平均作用温度与地表温度以及星上亮温做了分析,表明这些物理参数之间存在某种内在的联系。
2 深度动态学习神经网络和辐射传输模型解病态反演问题
地球物理参数之间的关系大多是非线性的,很难准确地用数学公式描述出来。从遥感数据中反演地球物理参数,由于其中非线性的关系和相互作用的因素很难描述清楚,传统的方法在简化的过程中使得反演精度下降。由于神经网络具备从复杂的和不精确的数据中提取信息,所以神经网络能够被用来提取模式和预测[30-31]。神经网络具备函数近似、分类和优化计算的能力,动态学习神经网络是解病态反演问题的最好方法之一。神经网络与传统的方法不一样,不需要准确知道输入参数和输出参数之间的具体关系。神经网络通过训练数据直接决定了输入数据和输出数据之间的关系。毛克彪等[29]分析表明地表温度和发射率能够通过3个热红外波段以及地球物理参数之间的关系来反演。该研究将针对MODIS的中红外和热红外波段进行模拟分析,利用辐射传输模型(MODTRAN4)和深度动态学习神经网络进行反演分析,找到分别适合于MODIS波段20/22/23(3~5 μm)和波段29/31/32/33(8~13.5 μm)数据的白天/晚上、白天、晚上地表温度反演方法。
MODIS波段20、22和23在中红外波段的窗口区,波段29~32在热红外波段的窗口区。虽然33波段在热红外波段窗口区的边缘上,但波段30受臭氧影响很大,因此波段30不适合反演地表温度。辐射传输模型(MODTRAN4)和深度动态学习神经网络执行反演分析可以简单地分为以下4步。
(1)利用MODTRAN4模拟训练和测试数据库,同时可以补充高精度的野外测量数据或MODIS温度产品;
(2)建立训练和测试数据库;
(3)计算波段20,22,23,29,30,31,32,33,利用MODIS波段2,5,17,18,19估算大气水汽含量;
(4)利用训练和网络反演地表温度。
利用MODTRAN4M模拟数据最大的优点在于能够很好地保证同一地物在MODIS波段20/22/23(3~5 μm)和波段29/31/32/33(8~13.5 μm)之间的发射率、水汽等不同物理参数之间的对应关系。利用JPL(URL:http://speclib.jpl.nasa.gov)测量的地物波谱曲线在MODIS波段20/22/23/29/31/32/33的发射率作为MODTRAN4的输入参数,地表温度变化范围为280~320 K和近地表空气温度变化范围为270~320 K。大气水汽含量变化范围0.2~4.0 g/cm2,观测视角0~20°之间。MODIS的观测视角为0~65°之间,可将其每隔20°建立一个训练数据库,根据角度范围选择不同的训练数据库,从而提高精度。为了简练,该文只分析0~20°之间的数据库分析过程情况,将模拟数据随机分成两部分:训练数据(33800组)和测试数据(15840组),然后用深度动态学习神经网络解病态反演问题。首先,用训练数据训练神经网络,然后用测试数据校验神经网络。根据地表类型和反复试验,部分测试数据信息见表1~11。
根据热红外波段和中外波段以及水汽波段的特征,划分成3组。第1组,适合白天和晚上的热红外波段组合,波段29/31/32/33(8~13.5 μm);第2组适合白天的热红外波段29/31/32/33(8~13.5 μm)和水汽波段;第3组是适合晚上的MODIS波段20/22/23(3~5 μm)与热红外波段29/31/32/33(8~13.5 μm)组合。
对于热红外波段29/31/32/33(8~13.5 μm),测试了不同的组合。表1是波段29-31-32组合,从表1可以看出,当隐含层数是5层且隐含节点为300-300-300-300-300时,平均精度最高为0.907 K,标准差为0.85 K,相关系数为0.995。
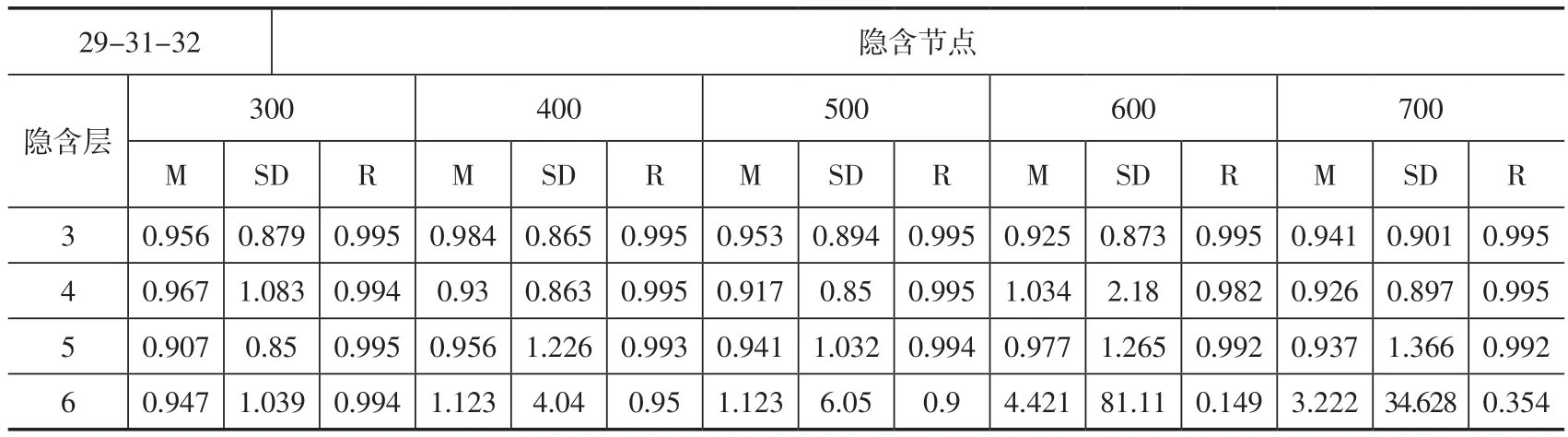
表1 波段29-31-32组合时反演误差Table 1 The Summery of Retrieval Error for band 29-31-32 combination
表2是波段29-31-32-33组合的误差表,从表中可以看出,当隐含层数是3层并且隐含节点为500-500-500时反演精度最高,最高平均精度为0.623 K,标准差为0.57 K和相关系数为0.998。从表1和表2可以看出,热红外波段增加可以提高反演精度。
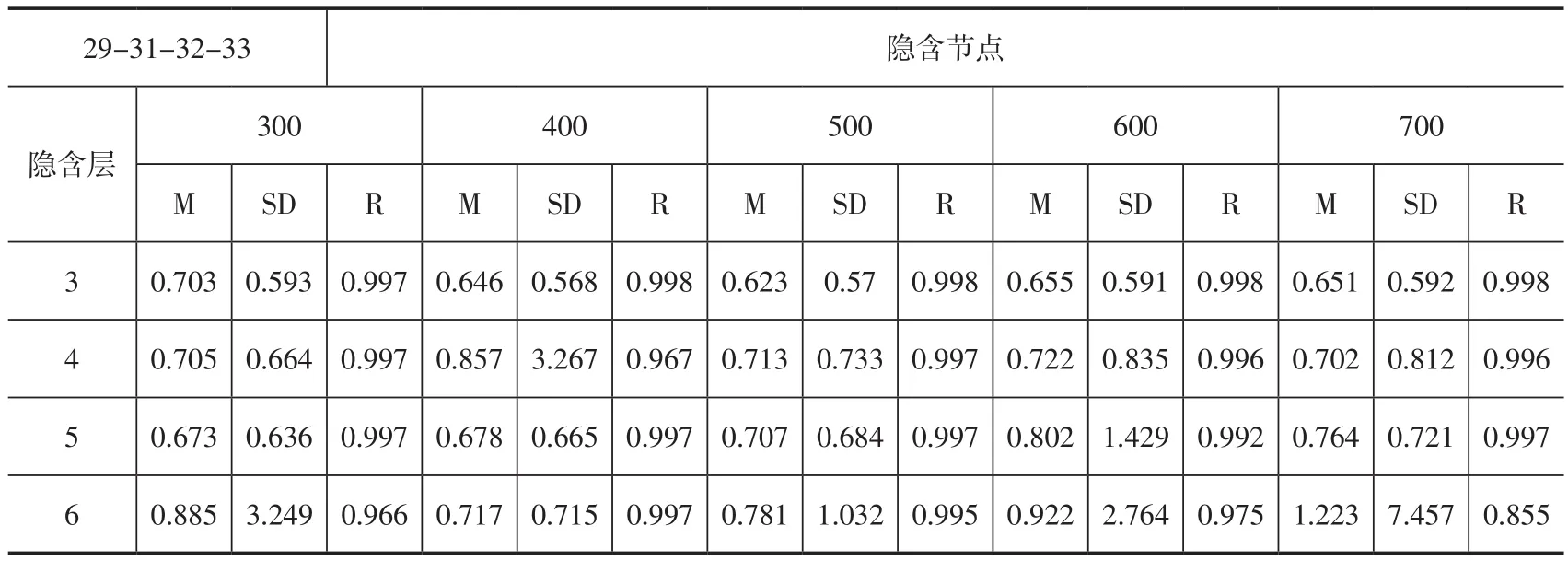
表2 波段29-31-32-33组合时反演误差Table 2 The Summery of Retrieval Error for band 29-31-32-33 combination
热红外波段加水汽(W)波段组合,主要适合于白天,因为水汽是从近红外波段估算得到。表3是MODIS波段29-31-32和水汽参数(W)作为深度学习神经网络的输入参数是反演误差部分信息表,从表3中可以看出当隐含层数是4和隐含节点是600-600-600-600时,反演精度最高。平均最高精度是0.251 K,标准差是0.255 K,相关系数是1。

表3 波段29-31-32-W组合时反演误差Table 3 The Summery of Retrieval Error for band 29-31-32-W combination
表4是MODIS波段29-31-32-33与W作为输入参数时的部分反演误差信息表,当隐含层数是4层并且隐含节点为500-500-500-500时精度最高,平均精度最高为0.302 K,标准差为0.273 K,相关系数是0.999。从表3和表4可以看出,当有水汽波段时,添加波段33时并没有提高反演精度。可以看出,水汽波段在地表温度反演中起到作用非常大。因此为提高地表温度反演精度,尽量添加大气水汽信息。
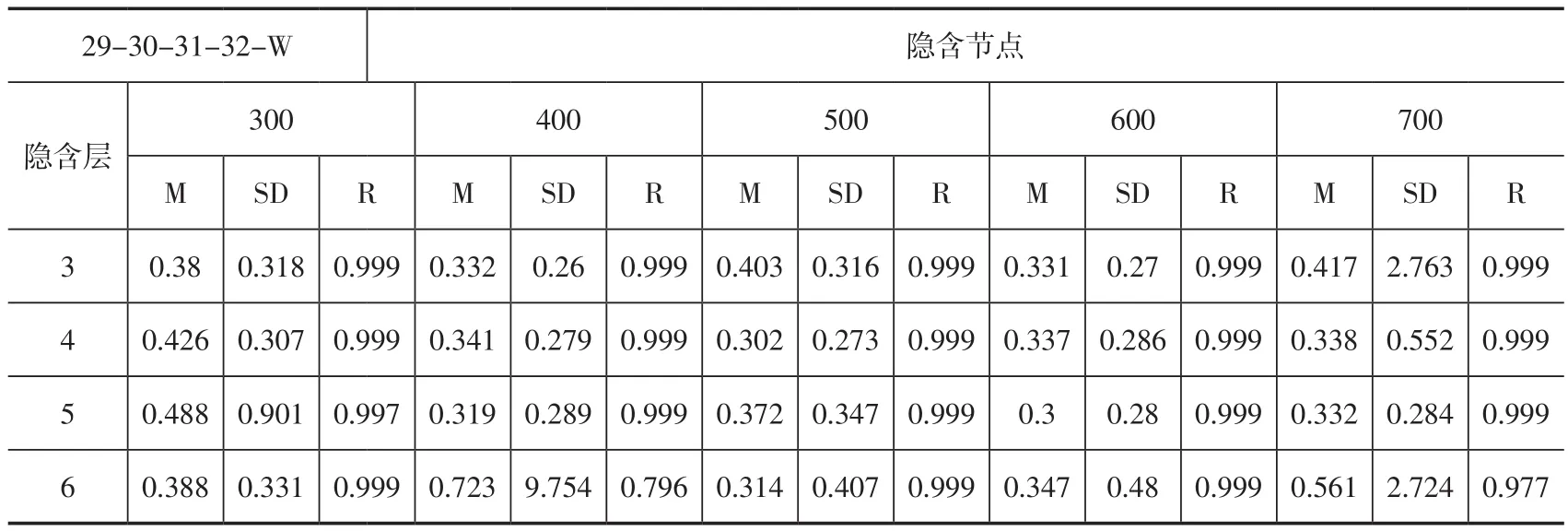
表4 波段29-31-32-33-W组合时反演误差Table 4 The Summery of Retrieval Error for band 29-31-32-33-W combination
中红波段20/22/23(3~5 μm)与热红外波段29/31/32/33(8~13.5 μm)的组合,由于中红外波段白天受太阳的干扰,因此中红外更适合在晚上反演地表温度。表5是波段20-31-32组合的反演误差信息表,当隐含层数是6层和隐含节点是600-600-600-600-600-600精度最高,为0.903 K,标准差为0.934 K,相关系数0.995。
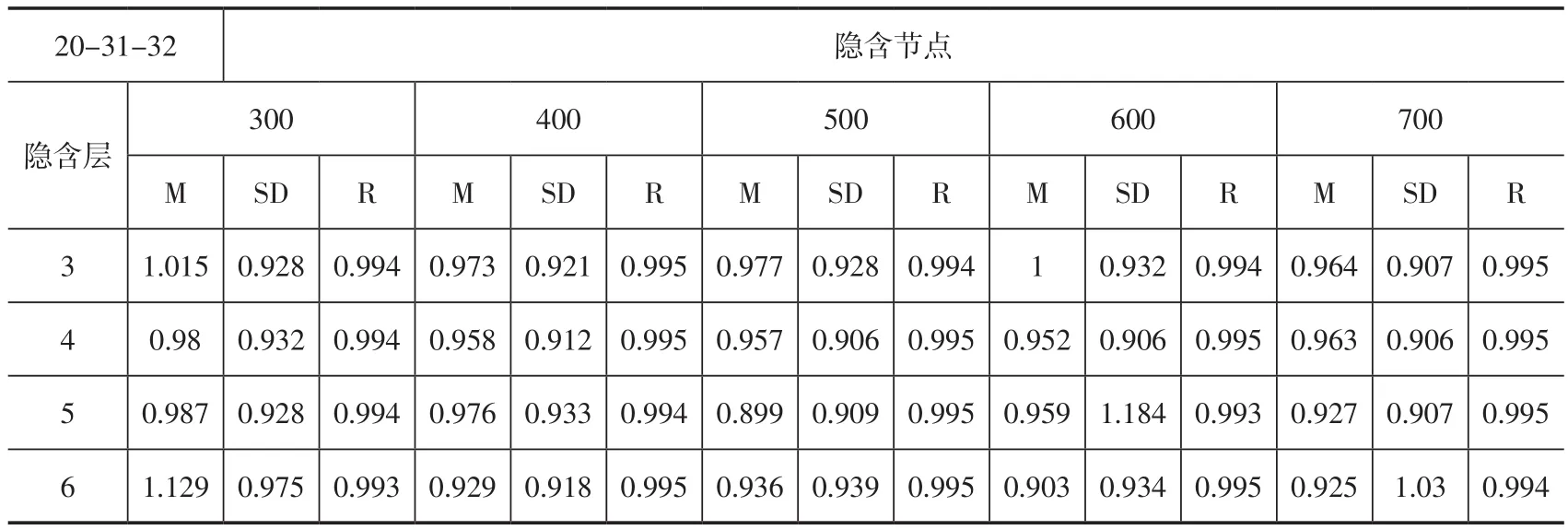
表5 波段20-31-32组合时反演误差Table 5 The Summery of Retrieval Error for band 20-31-32 combination
表6是波段20-29-31-32组合时的反演误差,最高精度是在隐含层数为3和隐含节点为600-600-600时,最高平均精度为0.568 K,标准偏差为0.608 K,相关系数为0.998。
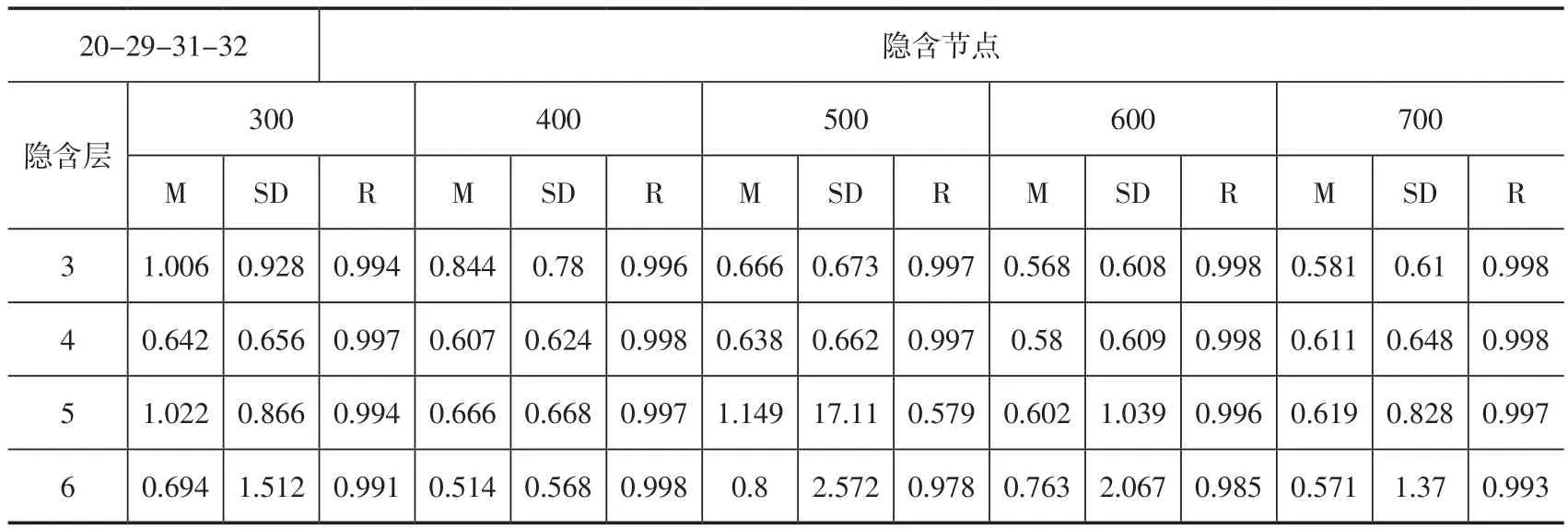
表6 波段20-29-31-32组合时反演误差Table 6 The Summery of Retrieval Error for band 20-29-31-32 combination
表7是波段20-22-31-32组合时的反演误差,最高精度是在隐含层数为4层和隐含节点为700-700-700-700时,最高平均精度为0.7 K,标准偏差为0.737 K,相关系数为0.997。对比表6和表7可知,利用热红外波段29比中红外波段22反演时候精度要高。

表7 波段20-22-31-32组合时反演误差Table 7 The Summery of Retrieval Error for band 20-22-31-32 combination
表8是波段20-22-29-31-32组合时的反演误差,最高精度是在隐含层数为6层和隐含节点为500-500-500-500-500-500时,最高平均精度为0.509 K,标准偏差为0.566 K,相关系数为0.998。
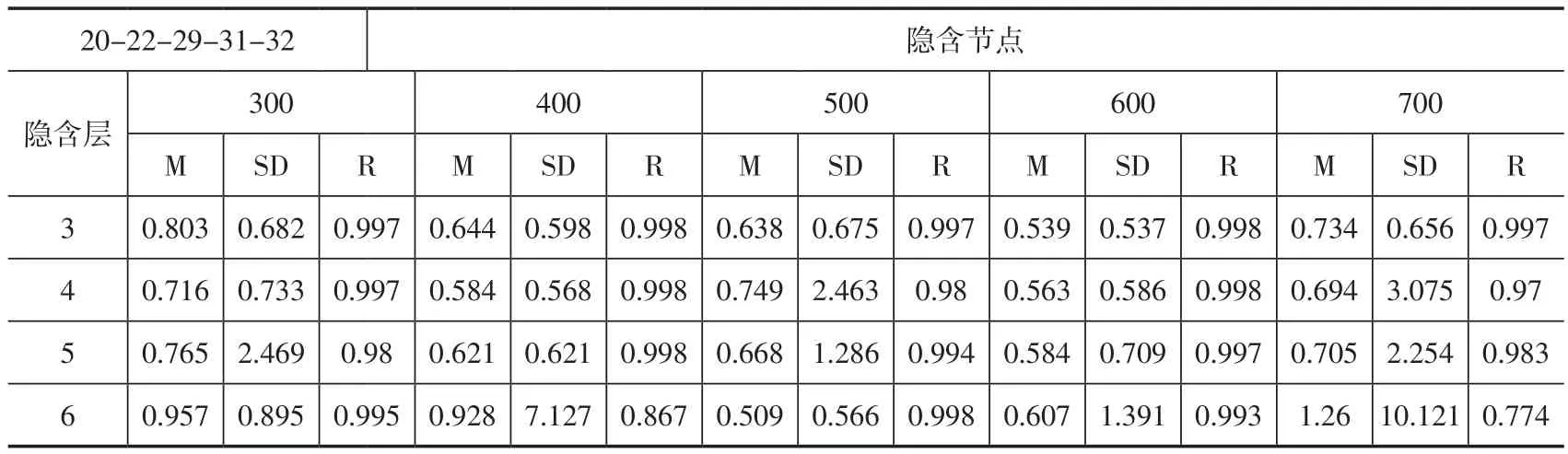
表8 波段20-22-29-31-32组合时反演误差Table 8 The Summery of Retrieval Error for band 20-22-29-31-32 combination
表9是波段20-22-23-29-31-32组合时的反演误差,最高精度是在隐含层数为5层和隐含节点为500-500-500-500-500时,最高平均精度为0.479 K,标准偏差为0.558 K,相关系数为0.998。
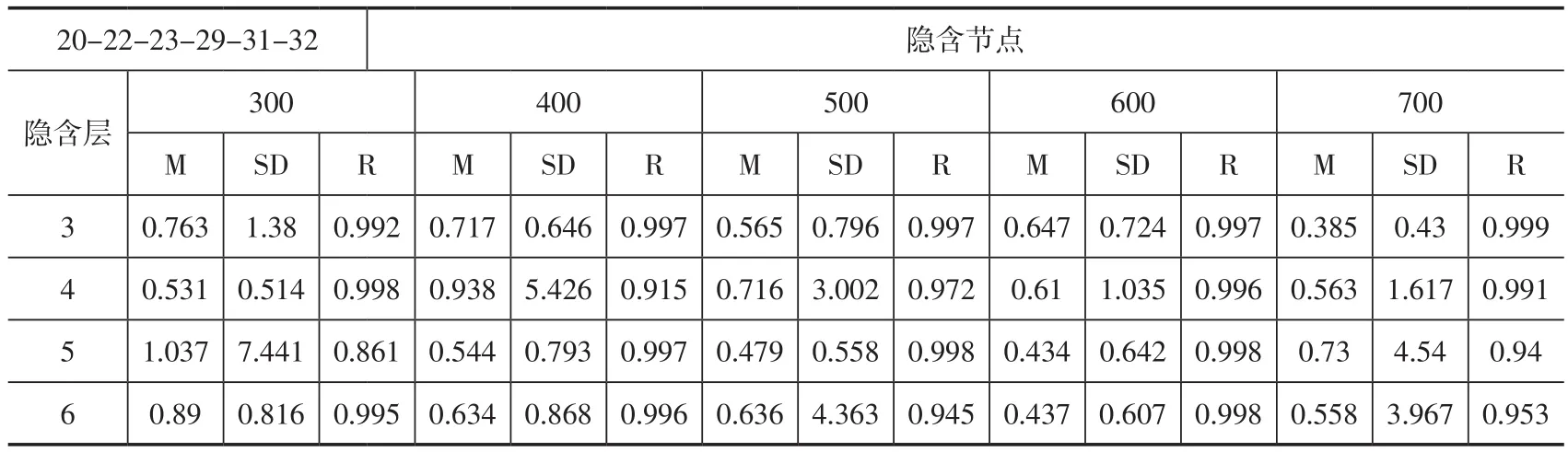
表9 波段20-22-23-29-31-32组合时反演误差Table 9 The Summery of Retrieval Error for band 20-22-23-29-31-32 combination
表10是波段20-22-29-31-32-33组合时的反演误差,最高精度是在隐含层数为5层和隐含节点为400-400-400-400-400时,最高平均精度为0.626 K,标准偏差为0.551 K,相关系数为0.998。对比表9和表10可以看出,利用中外波段23比利用红外波段33反演精度要高。

表10 波段20-22-29-31-32-33组合时反演误差Table 10 The Summery of Retrieval Error for band 20-22-29-31-32-33 combination
表11是波段20-22-23-29-31-32-33组合时的反演误差,最高精度是在隐含层数为4层和隐含节点为700-700-700-700时,最高平均精度为0.478 K,标准偏差为0.444 K,相关系数为0.999。对比表9和表11可知,利用7个波段(3个中红外波段+4个红外波段)与6个波段(3个中外波段+3个红外波段)的反演精度相当。由于第33波段受二氧化碳的影响比较大,从计算量角度讲,利用20-22-23-29-31-32波段组合更合适。
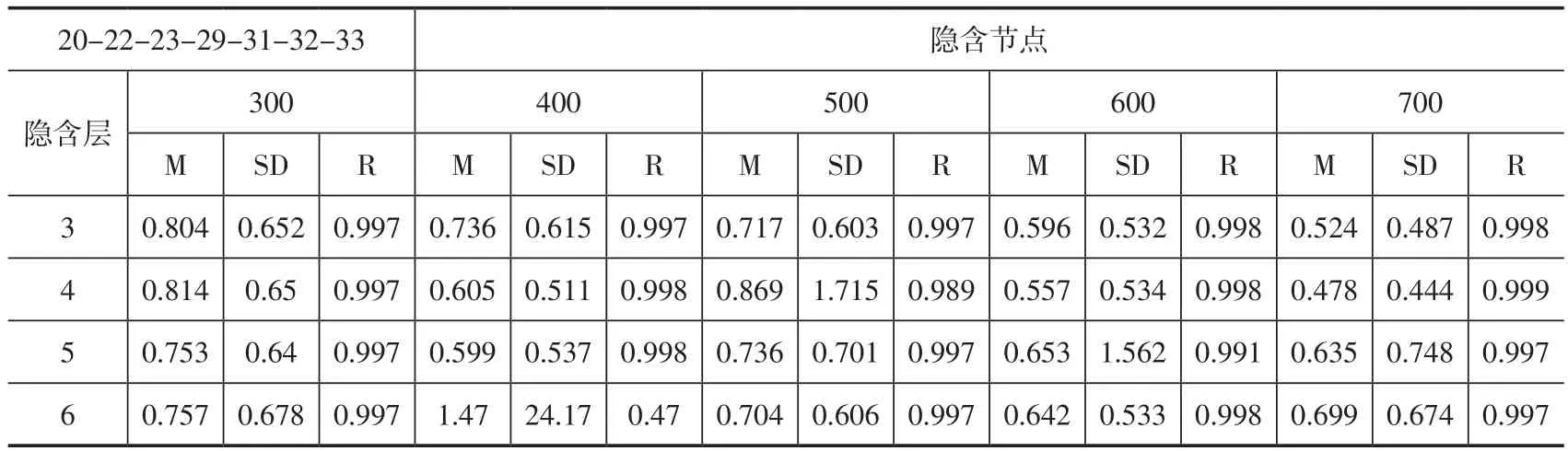
表11 波段20-22-23-29-31-32-33组合时反演误差Table 11 The Summery of Retrieval Error for band 20-22-23-29-31-32-33 combination
3 结论
虽然地表温度反演是属于典型的病态问题,但地球物理参数之间存在着相互联系和相互约束的关系。这些关系不能严格地用数学方法来描述,这就决定了大气辐射传输模型和深度动态学习神经网络的集成是解决地球物理参数(地表温度)病态反演问题的最好方法之一。以MODIS中红外波段和热红外波段作为分析对象,利用MODTRAN对MODIS波段20/22/23(3~5 μm)和波段29/31/32/33(8~13.5 μm)数据的白天/晚上、白天、晚上进行了模拟,并利用深度动态学习神经网络进行了反演分析。
对于适合白天和晚上的反演组合,波段29-31-32-33组合比波段29-31-32组合反演精度要高,说明热红外波段增加可以提高反演精度;对于只适合白天反演组合,波段29-31-32与W组合比波段29-31-32-33与W组合精度更高,反演误差都在0.3 K以下,说明水汽参数做温度反演中起的作用非常大,另外当有水汽波段和3个热红外波段时,再增加热红外波段33不会提高反演精度;在利用中红波段20/22/23(3~5 μm)与热红外波段29/31/32/33(8~13.5 μm)反演晚上地表温度的组合中,波段20-22-23-29-31-32组合和波段20-22-23-29-31-32-33组合时的反演误差都在0.5 K以下,7个波段组合精度略高。由于第33波段受二氧化碳的影响比较大,从计算量角度讲,利用20-22-23-29-31-32波段组合更合适。通过分析发现,利用动态学习神经网络和辐射传输模型可以高精度地从单景MODIS数据中反演地表温度和发射率,并且克服美国NASA白天/晚上算法的缺陷,彻底解决了地表温度和发射率反演的难题。深度动态学习神经网络和辐射传输模型的结合在地表温度和发射率反演的研究成果为国产风云和高分热红外传感器地表温度反演提供了参考模式。
