多传感器微惯性测量单元标定技术研究

牛艳芳，李 龙

(陕西航天时代导航设备有限公司，宝鸡 721006)

0 引言

微机电系统(Micro-Electro-Mechanical Sys-tem，MEMS) 惯性传感器由于其质量、体积、功耗、抗冲击和大量程等方面的优势，在姿态测控、武器制导等军事及民用领域有着广阔的应用前景[1-3]。随着微惯性器件精度的提高，目前国内外众多公司和研究所均集中于研究和开发微惯性器件及微惯性测量单元[4-5]，如美国的Draper实验室、大西洋惯性系统公司、波音公司、美国的BAE系统公司、挪威的Sensonor等。

微惯性测量单元(Micro Inertial Measurement Unit，MIMU)通常包含三轴陀螺仪和加速度计，实时提供包含运动物体姿态和位置信息的6个独立惯性参数。3个敏感轴严格互相垂直才能构成空间的直角坐标系，保证每个轴向的运动输入对其他2个轴向传感器不造成干扰。而在生产和制造过程中，绝对的互相正交很难保证，且MEMS器件对温度敏感。因此，使用前需要对其进行标定，建立误差模型，在使用中进行误差补偿，减小误差影响[6-7]。大量的文献设计了相关的标定方案[8-12]。常采用的是分立标定法，借助双轴或三轴转台将加速度计和陀螺分别进行标定，而对每个敏感轴集成多个传感器的MIMU正交标定补偿技术鲜有论述。

本文基于设计生产的一款每个敏感轴集合两种类型MEMS传感器的惯性测量单元，提出了针对多传感器惯性测量单元的标定补偿方法。在详细推导了微陀螺和微加速度计各自标定原理的基础上，通过实际产品说明了标定方法的使用过程；同时也证实了利用本文所介绍的标定方法，可以准确地将非正交坐标系的多个微惯性器件输出信息变换到正交的载体坐标系下；再根据温度对零偏、标度因子等进行补偿后的输出，可为后续的姿态解算和导航计算提供载体坐标系下准确的角速率和比力信息。

1 多传感器微惯性测量单元的组成及工作原理

以组合导航相关理论为基础，构建了以DSP+FPGA为主控制器，基于MEMS微机械陀螺及微加速度计的MIMU；通过现场可编程门阵列(Field Programmable Gate Array,FPGA)的译码、控制能力，将A/D芯片采集转换的MEMS惯性传感器数据采集到数字信号处理器(Digital Signal Proces-sing,DSP)中,完成传感器的标定及误差补偿，用于供给后续开发人员继续研究。

由于测量精度及范围的要求，目前设计生产的一款MIMU由6个微陀螺和4个微加速度计组成。6个微陀螺包括大小两种量程，各3个；4个微加速度计包括1个小量程和3个大量程。在基座的3个正交面上，分别安装由1对大小量程陀螺组成的陀螺电路及3个大量程加速度计,并在选定的X面再安装1个小量程加速度计，各传感器敏感轴正向输出构成的坐标系满足右手定则。同一时刻，3个正交面上各敏感轴的陀螺和加速度计传感器只有一个输出值有效，用来测量沿此3个方向的角速度和比力。多传感器微惯性测量单元的工作原理如图1所示。

图1 多传感器微惯性测量单元的工作原理示意图Fig.1 The scheme of multisensor MIMU

2 微惯性测量单元的标定方法

在多功能三轴位置、速率转台上对自制的MIMU 进行参数标定及误差补偿。标定过程中，以安装产品的结构六面体正交系为基准，MEMS 传感器构成的三轴坐标系轴向定义与基准坐标系轴向一致，将产品安装于转台台面上，结构轴向坐标系与转台转动轴平行。

MIMU中加速度计的零偏、标度因数可通过不同位置下各个通道加速度计的输出值计算得到；陀螺仪的零偏、标度因数可通过测试静态输出及不同角速率值对应的陀螺仪输出值，再经最小二乘法进行一次拟合得到。

2.1 陀螺仪输出数学模型

试验发现，本产品的陀螺对g值不敏感，因此，陀螺g值敏感项参数可忽略。

陀螺仪标定方案如下：

1)将MIMU安装于转台台面中心，通过设置转台分别使单元的X、Y、Z轴竖直向上，设置转台为速率工作方式，分别绕X、Y、Z轴做恒定角速率试验。

2)在陀螺仪测试量程范围内，由负向最大测量值开始驻点测试，到正向最大测量值结束，测试步长根据实际情况选择，不低于20(°)/s。

3)每个测试点采集20s数据。

4)读取各通道陀螺仪输出值，代入陀螺输出方程，即可求得陀螺仪的零偏、标度因数和正交误差等参数。

根据MIMU 中集成的陀螺仪输出参数特性，在常温下建立MIMU 中陀螺仪输出数学模型如下:

UGX-UGX0=KXXGX-KYXGY-KZXGZ

(1)

UGY-UGY0=KYYGY-KXYGX-KZYGZ

(2)

UGZ-UGZ0=KZZGZ-KXZGX-KYZGY

(3)

式中，UGi为MIMU 绕i轴转动时陀螺仪实际输出的角速度，UGi0为i轴陀螺仪零偏输出，Kii为i轴陀螺标度因数，Kij(i≠j) 为i轴陀螺仪j轴向安装误差系数，Gi为MIMU 中i轴陀螺输出的速率。其中，i=X，Y，Z;j=X，Y，Z。

陀螺仪的零位可通过静态测试求均值得到；标度因数可通过最小二乘法一次拟合不同角速率值(如本文选取的5个典型角速率值30(°)/s、60(°)/s、100(°)/s、200(°)/s和300(°)/s)与对应角速率下的陀螺仪输出得到。

对各个轴向集成大小量程两种陀螺的MIMU，为求得Kij，将装在六面体上的MIMU三轴坐标系分别与转台转轴平行，每个轴向通过转台输入给定的正负速率值，建立给定速率点下X、Y、Z轴各个陀螺的输出差值矩阵，如表1所示。

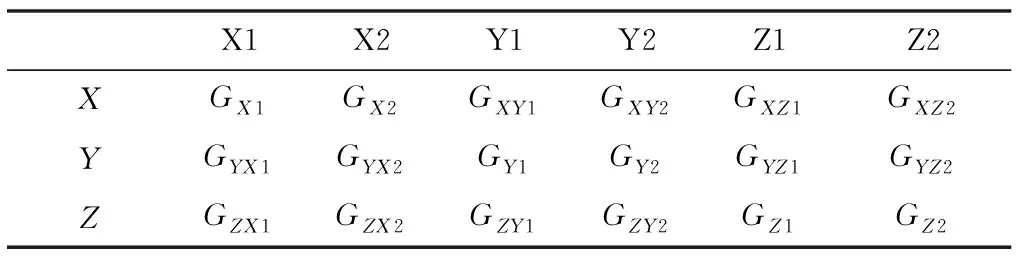
表1 X、Y、Z轴给定速率点时各个陀螺的输出Tab.1 Output of all gyros on axes X Y Z with constant rate

表1中，X1、Y1、Z1代表三轴向的小量程陀螺，X2、Y2、Z2代表三轴向的大量程陀螺，第2、3、4行分别表示X、Y、Z轴输入有变化时，3个轴向6个陀螺的输出变化值。此时，常温下MIMU中陀螺仪输出数学模型如下:

(4)

(5)

(6)

根据量程选择有效陀螺输出及计算陀螺交叉耦合系数E的参数值。当GX、GY、GZ的值大于给定阈值时，取X2、Y2、Z2的值作为有效值输出。此时，交叉耦合系数的计算参数分子的选取依赖于乘号后面的项，分母的选取依赖于多项式等号后面的第一项。

将陀螺仪输出零偏UGi0、标度因数Kii等参数代入式(4)～式(6)，进而可求得实际每个轴的陀螺输出。

2.2 加速度计输出数学模型

实验室环境中，加速度计静止不动时可敏感重力场中±1g范围内的加速度值，标定时采用六位置法进行标定。以X轴加速度计标定为例，确定加速度计标定方案：

1)将MIMU安装于转台台面中心，MIMU结构X轴垂直于转台台面，Y、Z轴与转台台面平行。

2)系统上电稳定后，开始测试。每位置测试20s数据，保证X、Y、Z轴每轴指天、指地各1次。

3)读取各个通道加速度计的输出值，根据不同位置点加速度计输出值计算加速度计零偏、标度因数和正交误差等参数。

根据MIMU 中集成的加速度计输出参数特性，在常温下建立MIMU 中加速度计输出数学模型如下:

UAX-UAX0=KXXAX-KYXAY-KZXAZ

(7)

UAY-UAY0=KYYAY-KXYAX-KZYAZ

(8)

UAZ-UAZ0=KZZAZ-KXZAX-KYZAY

(9)

式中，UAi为i轴加速度计输出，UAi0为i轴加速度计零偏输出，Kii为i轴加速度计标度因数，Kij(i≠j)为i轴加速度计j轴向安装误差系数，Ai为MIMU 中i轴加速度计输出的加速度。其中，i=X，Y，Z；j=X，Y，Z。

对于X轴向集成了大小量程两种加速度计，Y、Z轴各一个加速度计的MIMU，为求得Kij，将装在六面体上的MIMU进行六位置测试，如表2所示。

表2 六位置下各个加速度计的输出Tab.2 The output of all accelerometers on six positions

表2中，X1、Y1、Z1代表三轴向的大量程加速度计，X2代表X轴向的小量程加速度计，第2、3、4行分别表示X、Y、Z轴加速度计指天指地时，3个轴向4个加速度计的输出变化值。此时，常温下MIMU 中加速度计输出数学模型如下:

(10)

(11)

(12)

根据量程选择X轴加速度计出有效值AX。当AX的值大于给定阈值时，取X2的值作为有效值输出。此时，交叉耦合系数E参数分子和分母的选取均依赖于X轴加速度计的输出。

加速度计输出零偏UAi0及标度因数Kii可由六位置的加速度计数据计算得出。将求得的加速度计零偏、标度因数、交叉耦合系数代入式(10)～式(12)即可得到加速度计的实际输出。

3 MIMU测试标定方案

本文采用全温测试方法，所用MEMS陀螺能同时输出速率信号与温度信号，在-20℃、-10℃、0℃、10℃、20℃、30℃、40℃、50℃、60℃环境温度下，每个温度点保温2h，然后采集陀螺在不同速率点下的输出信号与温度输出信号、加速度计与陀螺在6个位置的输出信号与温度输出信号。试验发现，在不同的温度点陀螺零偏及加速度计零偏有较大波动。因此，需按温度对它们的零偏进行补偿。

通过大量的试验分析，文中选用了一种基于温度的陀螺及加速度计分段补偿方法，即在温度区间选取一系列温度点；然后测得各温度点的零偏及刻度因子，按温度区间分段拟合零偏及刻度因子与温度的关系；最后根据实测温度符合的温度区间，选取相应区间的拟合直线计算当前零偏及刻度因子。

(13)

式中，j取值1，2，…，9，为全温区间选取的各个温度点的序号，Tj为各温度点的数字量，Gj为各温度点下陀螺(加速度计)的零偏或刻度因子数字量，T代表当前的陀螺(加速度计)温度数字量。

在实际应用中，通过高低温试验,确定每个陀螺和加速度计的Tj、Gj；在常温下测试并计算陀螺及加速度计的相关交叉耦合系数，将这些参数固化在内部DSP系统中，在陀螺开机后测出陀螺温度T，即可以通过式(13)估计出陀螺和加速度计的当前零偏及刻度因子；然后再从实测零偏中减去该估计出的零偏并除以刻度因子，就可以得到补偿后的零偏。按式(4)～式(6)及式(7)～式(9)可以得到补偿后的陀螺及加速度计实际输出。通过编写的VC软件对标定补偿后的数据进行采集，计算得到补偿后的加速度计和陀螺仪的各项指标数据。

4 试验结果及分析

零偏、刻度因子及交叉耦合系数试验是在高低温三轴转台上进行的，温箱控制范围为-40℃～70℃，完全可以满足试验要求。在-40℃、-20℃、-10℃、0℃、10℃、20℃、30℃、50℃、70℃环境温度下，每个温度点保温2h，然后采集6个陀螺在选定速率点下的输出信号与温度输出信号、4个加速度计在6个位置下的输出信号与温度输出信号。

利用2.1节和2.2节中的方法便可以对陀螺及加速度计进行实时补偿，为此在常温下做了零偏测试试验和速率测试试验，测试时间为1h，取得了比较理想的补偿效果。以X轴陀螺为例，零偏测试结果如图2所示，速率测试结果如表3所示。

图2 补偿前后陀螺输出Fig.2 Output of gyro before and after compensation

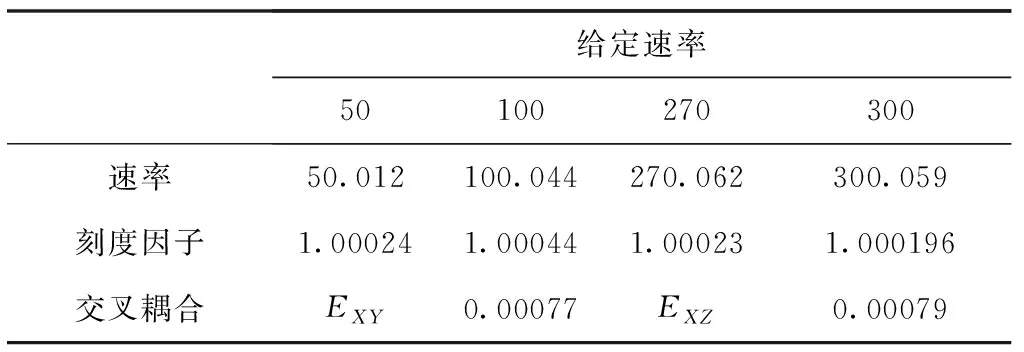
表3 X轴陀螺常温下在不同速率点的输出及得到的相关参数Tab.3 Outputs and parameters of X gyro with different rates

270(°)/s是大小量程陀螺输出的切换点，由表3可以看出，补偿后的陀螺在不同速率点的刻度因子在1±0.001以内，交叉耦合系数在1‰以内，得到了显著的补偿效果。

对补偿前后的补偿系数进行对比，如表4所示。

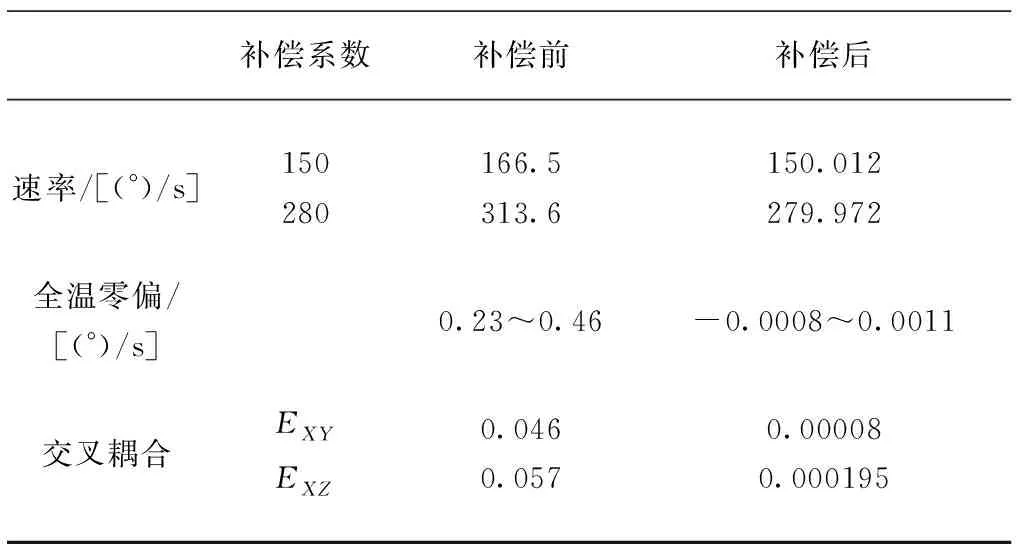
表4 X轴陀螺补偿前后相关系数对比Tab.4 X gyro parameters before and after calibration

由表4可见，全温补偿后的零偏全温变化范围为-0.0008～0.0011，对比补偿前的0.23～0.46，减小很多；再对标准角速率点150和280的输出数据进行对比，可见补偿后的输出更接近标准值，此时刻度因子更接近1；同时在X轴转动时，对Y、Z轴的影响由0.046～0.057减小为0.00008～0.000195。分析可知，补偿后的陀螺仪标定系数精度比补偿前提高了几个数量级。

5 结论

正确地对微惯性测量组合进行标定和误差补偿，是有效使用微惯性测量系统的前提和关键。本文基于设计生产的一款多MEMS传感器集成的惯性测量单元，提出了针对多传感器惯性测量单元的标定补偿方法。与传统方法相比，多传感器的使用保证了用户的量程需求和精度要求，节约了成本；在此基础上，该标定方法简化了MIMU 的标定步骤，缩短了标定时间。实验证明，采用该标定补偿方法后，MIMU的测量精度可提高1～2 个数量级。