基于应力松弛试验的人牙周膜五参数粘弹性模型构建
2019-01-25吴斌鹿如鑫严斌谢理哲赵思雨黄辉祥杨宇汤文成
吴斌,鹿如鑫,严斌,谢理哲,赵思雨,黄辉祥,杨宇,汤文成
(1.南京林业大学 机械电子工程学院,江苏 南京 210037;2.南京医科大学 口腔疾病研究江苏省重点实验室/南京医科大学附属口腔医院 正畸科,江苏 南京 210029;3.南京工程学院 机械工程学院,江苏 南京 211167; 4.东南大学 机械工程学院,江苏 南京 211189)
获得牙周膜在矫治力作用下的响应是研究正畸过程中牙齿移动机制的关键。受制于人体口腔特殊环境,直接测量牙周膜受力后的应力应变尚无法实现,数值仿真成为重要手段[1]。但是,牙周膜厚度为0.15~0.38 mm[2],主要由胶原纤维(占53~74%)、细胞、血管(占1~2%)和基质组成[3],复杂的内部构成导致目前尚无公认的、能准确描述其力学特性的材料模型,直接影响了仿真的精确度。合理的材料模型的建立依赖于完善的力学实验,已有的一些实验[4- 10]虽然表明了牙周膜具有典型的非线性粘弹性特征,但多为动物实验[11- 13],数据存在较大偏差,且没有获得具体的模型参数。人体牙周膜的相关试验尚处于探索阶段,以静态试验为主,尚未见基于时间相关性的专用于描述其粘弹性特征的实验。作者通过对人体牙周膜切片进行应力松弛实验获得其松弛模量曲线,再基于粘弹性理论构建了一个五参数固体粘弹性本构模型,来描述其粘弹性力学行为中的应力松弛效应,并求解了模型的具体参数。
1 材料和方法
1.1 样本制备
实验用6例上颌前牙牙周膜样本取自人颌骨[尸体样本来自南京医科大学解剖学系(南京医科大学伦理审核(2015)169号)]。制作切片前记录样本来源、患者年龄、性别等,去除附着在人颌骨的软组织备用。样本来源于1986年男性尸体,无牙周病史。由于人牙与动物牙齿比较相对较小,如果选用多牙根的磨牙,不易制作出样本,且样本不易夹持,故一般选用单牙根的中切牙或侧切牙。样本制备流程如下:(1)分离目标牙齿并尽量保持牙齿周围的牙槽骨完整,如图1a。(2)使用慢速骨锯垂直于牙长轴,在牙槽嵴附近将牙冠部分切除,同时在牙根尖部位垂直于牙长轴将牙根以下部分切除。根据牙齿实际长度,将同颗牙齿切成3份薄片,如图1b,并记录薄片具体位置(根颈部、根中部、根尖部),得到的薄片如图1c所示。(3)平行于牙长轴方向将薄片切割为小矩形块,如图1d虚线所示。将切割好的样本置于生理盐水中,-20 ℃条件下保存。实验当天从冷冻室中取出样本于室温下解冻,如图1e,并用电子千分尺测量试验样本的精确尺寸。本研究使用的所有试样在试验期间均只冷冻和解冻1次,以保持样本的机械性能[13]。制作好的人牙周膜样本包含牙齿、牙周膜和牙槽骨3部分,牙齿和牙槽骨端作为夹持端,以便于单轴拉伸实验的进行。样本信息如表1所示。
1.2 实验装置
本试验仪器选用微机控制电子万能材料实验机[CTM2010,协强仪器制造(上海)有限公司]。由于样本尺寸较小,安装时需小心轻柔以免损坏样本,将样本的牙槽骨端和牙齿端在试验机夹具的固定端夹紧,露出牙周膜。实验中,采用位移控制,滴加生理盐水进行保湿。
1.3 实验过程
在正式试验开始前,需要对样本进行预加载[9]。研究[14]表明,人的平均咀嚼频率约为1.57 Hz。本试验通过以1 Hz的频率,0.1应变的振幅20次谐波循环对其进行预处理。约10个周期的循环加载后,试样呈现稳定的应力应变状态,这与Sanctuary[15]的研究结果相同。
应力松弛指材料受恒定应变时应力随时间减小的现象,这意味着材料应受位移载荷的控制。由连续介质力学对应力松弛的定义可知,应力松弛实验应施加阶跃应变载荷,以探究材料在瞬时载荷下的应力响应,无法实现Sanctuary[15]在文中提出实际试验时瞬时跳跃的载荷,如图2a所示,应尽量的减少加载时间t*,即应尽可能的提升拉伸阶段应变率。经多次尝试,在不引起仪器振动而使数据产生振荡的前提下,加载时间设置为3 s。为体现材料的粘性特征,应力松弛的应变参数不宜设置的过小,应在牙周膜纤维完全拉伸并被动延展的阶段选取,以跳过牙周膜的瞬时弹性特征,本试验选取拉伸的应变为0.4,保载200 s(过长的保载时间会导致样本失去水分,200 s为多次预实验后总结获得的合理时间)。加载曲线如图2b所示。

图1牙齿-牙周膜-牙槽骨切片样本制作流程示意图
表1牙齿样本基本参数
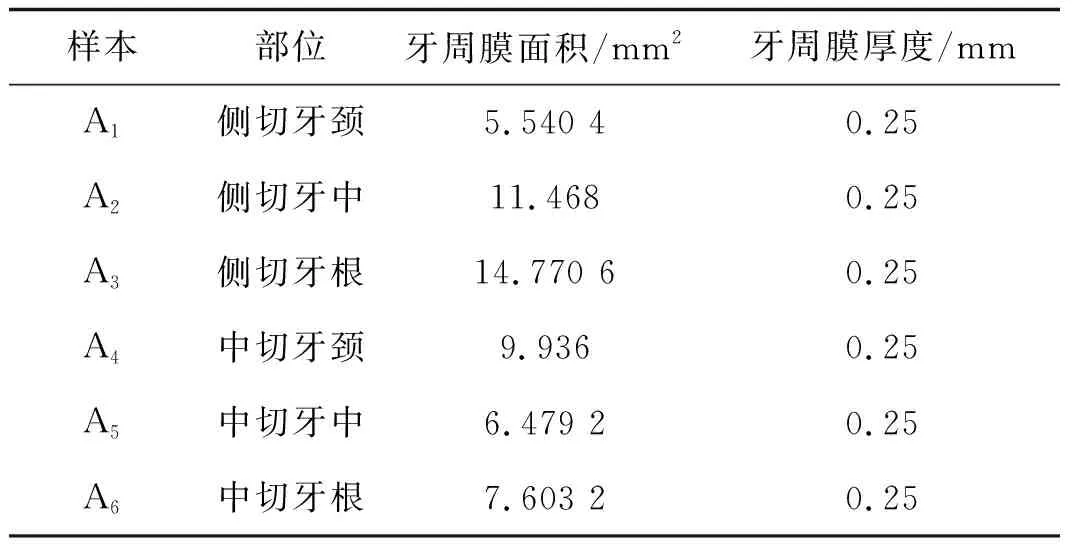
样本部位牙周膜面积/mm2牙周膜厚度/mmA1侧切牙颈5.540 40.25A2侧切牙中11.4680.25A3侧切牙根14.770 60.25A4中切牙颈9.9360.25A5中切牙中6.479 20.25A6中切牙根7.603 20.25
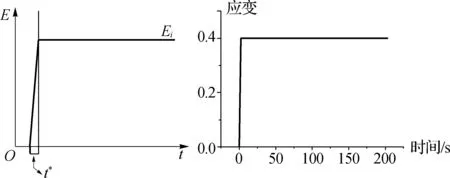
a.理想加载曲线 b.应力松弛实验加载曲线
图2加载曲线
1.4 数据处理
首先计算试样所受的Lagragian应力σx[16]:
(1)
式中Fx为实验所记录的沿拉伸方向的拉力,A为拉伸方向的参考截面积(通过实验前测量的样本尺寸计算得到)
计算各时刻应变ε:
(2)
式中d为实验所记录的沿拉伸方向的位移,d0为试样牙周膜的厚度(此处取平均厚度0.25 mm)。
各样本应力与时间的关系,如图3所示。同时为求取模型参数,根据公式(3)计算得到实验数据的松弛模量曲线。
(3)
从样本应力- 时间曲线可以看出,样本在受到阶跃位移载荷时,应力响应并非随时间不变,而是随时间缓慢变小且开始阶段趋势明显,150 s以后曲线逐渐趋于平缓,体现出牙周膜材料应力响应随时间变化的形式,表明其粘弹性特征。
未来,围绕短视频可以开展更多的场景化营销,甚至可以与其他的媒体平台进行整合,在今天这样一个轻量化的内容营销的时代,短视频尤其是原创性短视频是这个轻量化内容营销时代的重要入口,抓住这个人口,就是占据了潮流,就会成为消费者心目当中最热爱的那个品牌。
2 模型的构建及参数求取
应力松弛是粘弹性材料的典型特征之一[17],应力松弛响应可表示如下:
(4)
相应的,蠕变响应也可表示为:

图3应力-时间曲线
(5)
式(3)和(4)中,G(t)与J(t)分别为应力松弛模量与蠕变柔量
从粘弹性材料的本构关系不难发现,蠕变柔量J(t)和松弛模量G(t)之间的关系可以通过式(6)中的拉普拉斯变换式来进行推导,
(6)

2.1 Zener模型
广义粘弹性模型主要包括广义Maxwell模型(也称为Wiechert模型)和Kelvin链模型。广义Maxwell模型是由多个并联的Maxwell模型与退化单元弹簧元件或粘壶元件进一步并联组成,该模型适合描述松弛现象;Kelvin链模型是由多个串联的Kelvin模型元件退化单元串联而成,较为适合描述蠕变现象。本课题组成员Huang[12]曾提出了Zener模型用于描述牙周膜的粘弹性力学行为,该模型为Maxwell单元并联一个弹簧元件。
(7)
获得松弛模量G(t)为:
(8)

2.2 五参数模型
建模时应考虑材料本质更偏向于流体还是固体以及材料对突变载荷的瞬态响应。由粘弹性理论可知,通过增加参数量可以提高模型对粘弹性力学行为的描述能力。本研究在课题组已建立的三参数固体粘弹性Zener模型基础上进一步构建了五参数有冲击响应的固体粘弹性模型,其组成形式如图4所示。

图4五参数固体粘弹性模型
设弹簧柔度分别为E1、E2、E3,粘壶粘度为η1、η2,整个系统所受的应力为σ,应变为ε。根据组成部分之间的关系,列出如下的线性微分方程组:
(9)
对微分方程组进行Laplace变换,消去中间变量σ1、σ2、σ3,得:
(10)
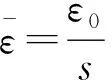
(11)
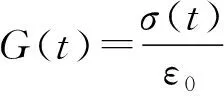
(12)

2.3 模型对比及参数求取
根据试验所获得的应力-时间曲线,由式(3)计算得到试验过程中牙周膜的松弛模量G(t)曲线。为了评价Zener模型和五参数模型对牙周膜应力松弛特征的描述能力,分别用式(8)和式(12)对松弛模量曲线进行拟合。由于不存在理想的阶跃加载过程,故拟合时忽略加载过程的数据点,仅从达到预设应变载荷处开始拟合,各样本拟合结果如图5所示,残差分布如图6所示,拟合优度见表2。
从图中可以看出Zener模型与牙周膜的应力松弛特性符合度相对较高,校正决定系数在0.93至0.98之间。但是,进一步观察残差分布图时发现,Zener模型残差分布范围较大且离散程度不高,曲线刚开始的一段尤为明显。表明三参数固体粘弹性Zener模型在一定程度上可以描述牙周膜非线性粘弹性行为,但仍不精确。与Zener模型相比,五参数固体粘弹性模型对实验数据的拟合精度有了很大提高,校正决定系数均在0.99以上。最重要的是,残差分布范围缩小一半,且残差分布离散程度更高,能够更好的表现实验曲线开始阶段的骤降现象。这表明五参数固体粘弹性模型比Zener模型更适合用于描述牙周膜的粘弹性力学行为。
进一步将试验数据代入五参数模型松弛模量公式(12),可以计算得到各个样本的模型参数(表3)。
3 讨 论
牙周膜的粘弹性力学特征非常复杂,受制于实验的困难性以及人牙周膜复杂的内部构成,目前尚无公认的、能准确描述其力学特性的材料本构模型。牙周膜本构模型的构建需从材料本身的特性出发,考虑到牙周膜的组成成分中纤维占比重最大,偏固体的粘弹性模型更加适合描述其力学特性;从试验数据可以看出,牙周膜在突变载荷下会产生瞬态响应。如果使用Kelvin链的形式构建多参数的本构模型,则需要退化的粘壶单元且不需要退化的弹簧单元;如果使用广义Maxwell模型,则无退化的粘壶单元可保证有冲击响应,有退化的弹簧单元可使模型具有固体特性。
本研究在已有的Zener模型的基础上并联了一个Maxwell单元,引入了一个新的五参数粘弹性模型来描述牙周膜的应力松弛特征。通过万能材料实验机对人牙周膜样本切片进行单轴拉伸,获得了牙周膜应力松弛试验数据,从实验曲线可以看出牙周膜材料应力响应随时间缓慢变小且开始阶段趋势明显,150 s后曲线逐渐趋于平缓,表明其粘弹性特征。为对比Zener模型与五参数模型的描述能力,分别使用松弛模量公式对试验数据进行最小二乘法拟合分析。通过拟合对比可以看出,Zener模型能在一定程度上描述牙周膜的粘弹性力学行为,但残差分布不离散且分布较大,在曲线开始阶段尤为明显。而五参数模型的拟合精度有了很大提高,校正决定系数均在0.99以上,同时,五参数模型的残差范围比Zener模型小一个数量级。通过残差分布图可以看出,相比与Zener模型,五参数模型能够更好的体现出松弛模量(应力)在开始阶段骤降的现象。这表明五参数固体粘弹性模型比Zener模型更适合用于描述牙周膜的粘弹性力学特性。这种结果是可以预见的,因为模型参数越多,模型通过参数的自我调整能力越强,对实验曲线的拟合能力越强,同时模型的计算机编程实现难度也越大。通过本研究可以看出,五参数模型已经能够很好地拟合实验数据,从而没有必要继续追求更高参数的粘弹性模型,以免增加材料模型的有限元实现难度。但是,由于人体实验样本获取不易,且对实验环境要求较高,本次实验样本数较少。现有的人样本牙周膜生物力学研究绝大多数以单根牙为研究对象,多根牙样本基本没有,这是由于牙根形态不同,牙周膜面积差异很大,不同于牛、猪的牙齿,人牙齿很小,单根牙切片样本相对容易制作,而本来就很小的牙齿在多根形态下极难制作出可供试验的切片样本,牙齿和牙槽骨太短不易夹持,切片损坏率太高,因此本研究以单根牙为研究对象。在实际情况中不同部位的牙周膜承受的牙合力确实不同,然而,牙周膜的组织形态、基本构成不因位置而改变,不同部位的牙周膜受力时应力应变变化的具体数值存在差异,但其基本趋势一致。即便如此,由单根牙样本试验数据拟合得到的模型是否适用于多根牙,仍需进一步的试验验证。后续研究将进一步扩大样本容量并结合临床实际,对本研究提出模型做进一步的验证。

图5Zener与五参数模型拟合对比
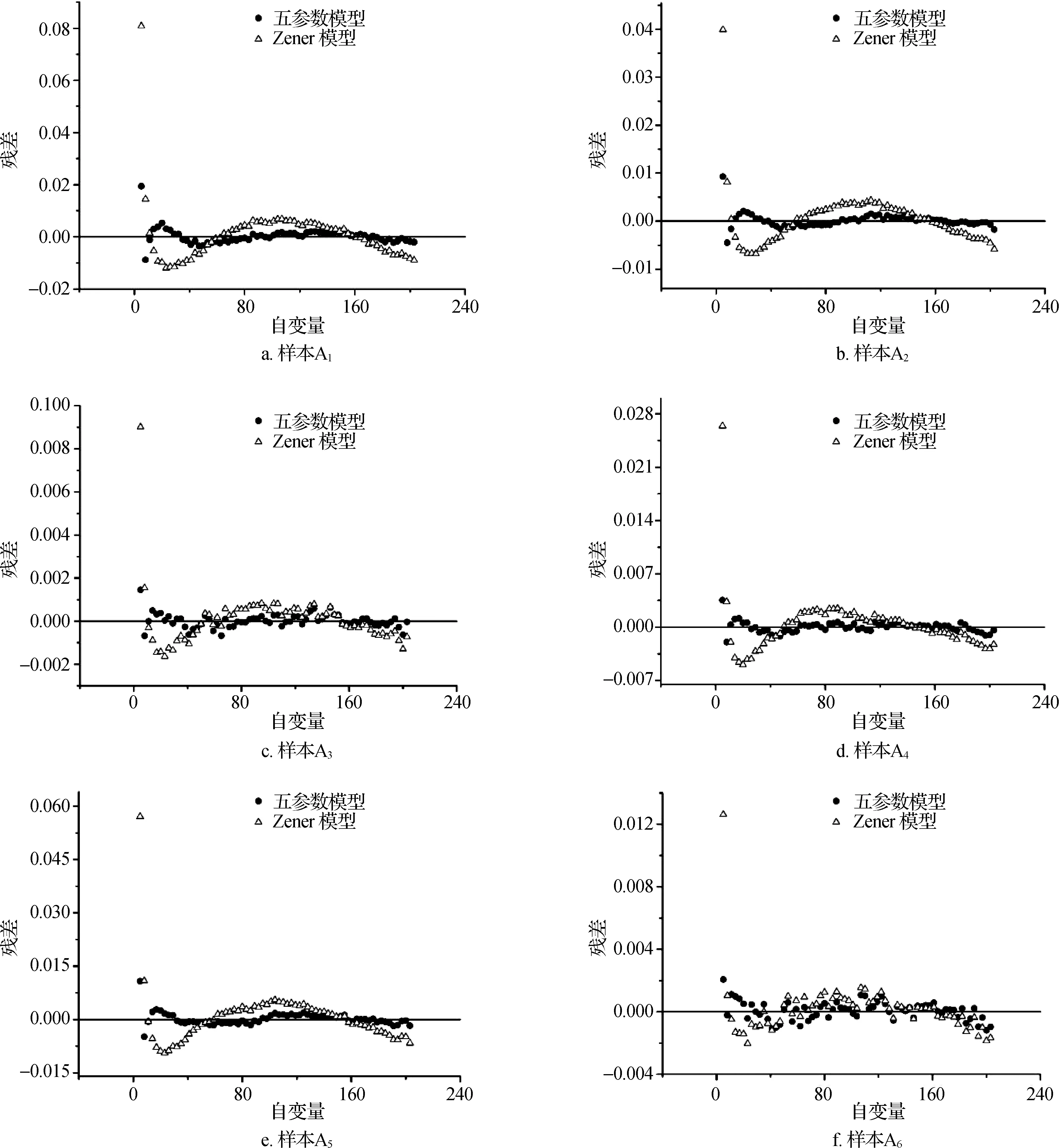
图6Zener与五参数模型残差分布对比
表2拟合优度对比
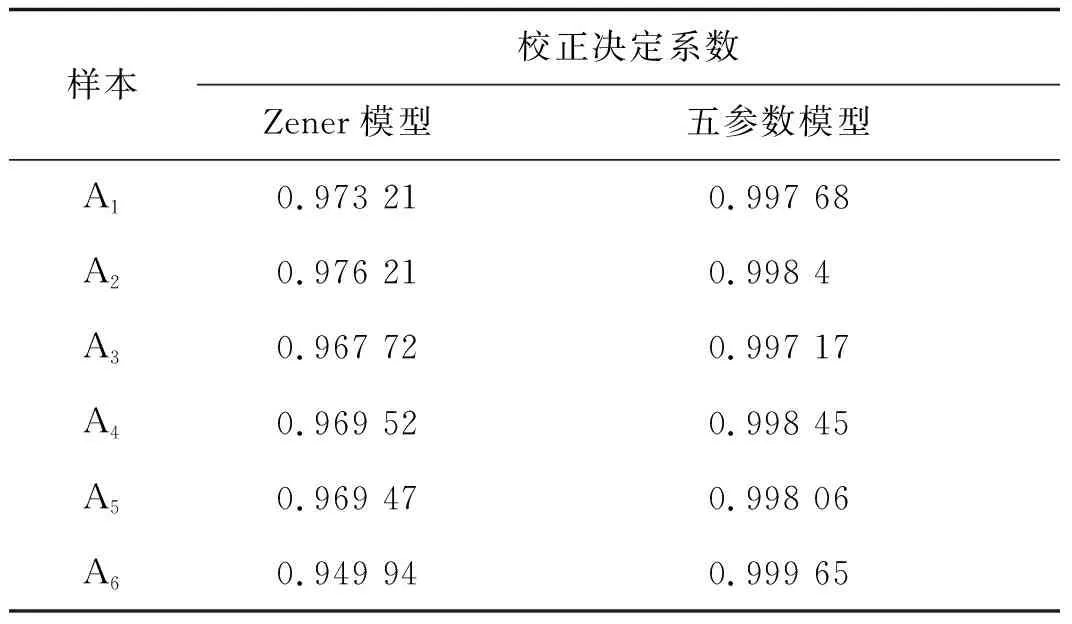
样本校正决定系数Zener模型五参数模型A10.973 210.997 68A20.976 210.998 4A30.967 720.997 17A40.969 520.998 45A50.969 470.998 06A60.949 940.999 65
表3模型参数
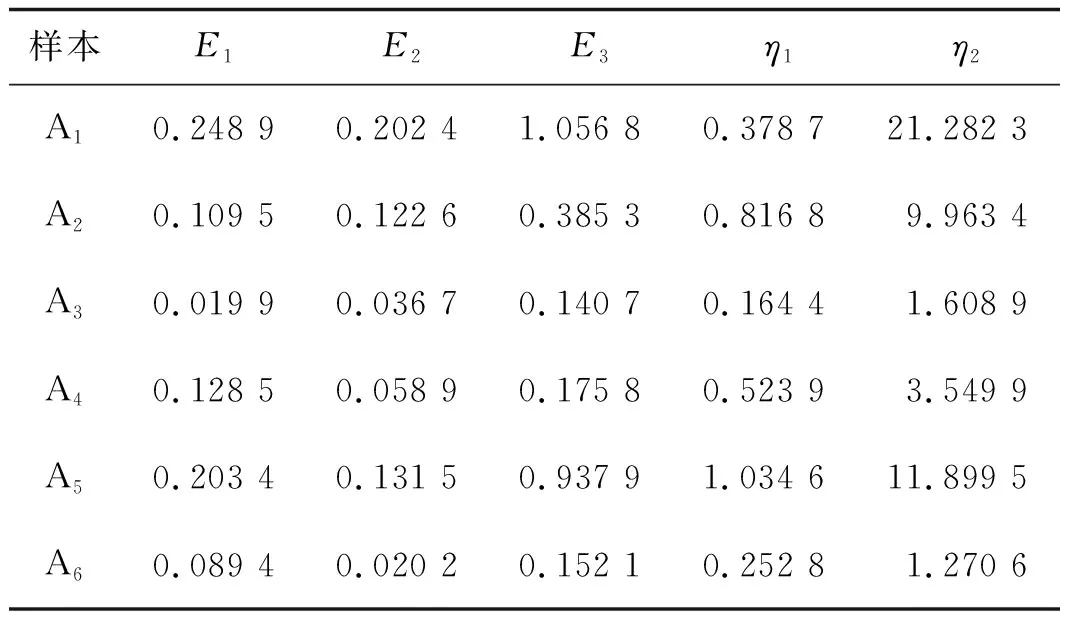
样本E1E2E3η1η2A10.248 90.202 41.056 80.378 721.282 3A20.109 50.122 60.385 30.816 89.963 4A30.019 90.036 70.140 70.164 41.608 9A40.128 50.058 90.175 80.523 93.549 9A50.203 40.131 50.937 91.034 611.899 5A60.089 40.020 20.152 10.252 81.270 6
