卷积理论在海铁联运衔接可靠性中的应用

李红雨 袁韵美 南京铁道职业技术学院

张 琦 北京交通大学

1 卷积理论及其在可靠性中的运用

卷积（Convolution）是分析数学中一种重要的运算，是两个变量在某范围内相乘后求和的结果，可作为两个函数fg成第三个函数的数学算子，用来表征函数f经过翻转和平移的g叠部分的累积。一般情况下，常直接采用卷积的数学定义来求解问题。

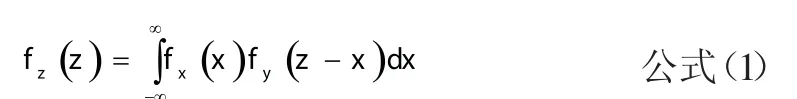
卷积理论在工程领域及数学领域都有很广泛的应用。在统计学中用于计算加权的滑动平均值，在概率论中用于计算两统计变量之和的概率密度函数，在声学中用于确定源声与一个反映各种反射效应的函数，在物理学与电子工程学中用于确定任意一个线性系统的输出。但目前卷积理论在运输系统中两系统衔接可靠性方面的应用较少，本文将把卷积理论应用于海铁联运衔接可靠性并分析其应用效果。

2 于卷积理论的海铁联运衔接可靠性指标计算

在保证运量的前提下，海铁联运衔接过程的可靠性体现发车成本与集装箱等待时间的适应性及班列开行方案与随机变化的集装箱运量的适应性两方面。基于上述总体目标，确定其可靠性指标主要包括实际开行班列数、丢线数、增发班列数、时间成本、发车成本、综合成本。本章将结合卷积理论对以上指标进行计算分析。

海铁联运衔接可靠性指标计算的难点在于如何确定本次集结周期末在站剩余集装箱数，这不仅取决于本周期内随到港船舶到达、并转场到港前铁路车站堆场的集装箱数，还取决于上一个周期末的在站剩余集装箱数，而本周期末的在站剩余集装箱数也会对下一个周期产生影响，如此循环。本文应用卷积理论，对这种复杂的动态循环过程进行分析，以便确定在统计时间范围内每个循环周期中的在站剩余箱数，本文应用卷积理论测算本次集结周期末在站剩余集装箱数，考虑以集结周期Ti、周期Ti+1为基础，考虑集结周期Ti+1的剩余箱数Ii+1对下一个周期Ti+2的影响，则周期Ti+2内剩余箱数概率与期望的计算公式为：

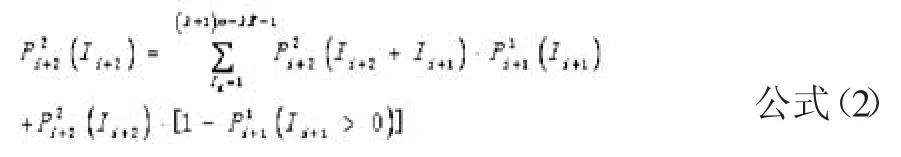
其中:

Ii—在周期 结束时，剩余的集装箱数，单位：TEU；

M，m—集装箱班列最大最小编成辆数限制数，单位：TEU；

Pi（x）—在周期i内到达集装箱数为x的概率；

将应用卷积理论测算的本次集结周期末在站剩余集装箱数作为基础，海铁联运衔接可靠性指标计算公式如表1所示。

表1 海铁联运衔接可靠性指标计算公式

3 铁联运集装箱班列开行方案的确定

从集装箱由海路到达港口直到到集装箱在铁路装车站装车出发的过程中，缩短集装箱在站场的等待时间是优化海铁联运集装箱班列开行方案的核心目标。以等待时间为目标函数，以每一周期的运量和班列编成辆数作为约束条件构建海铁联运集装箱班列开行方案优化模型如下：

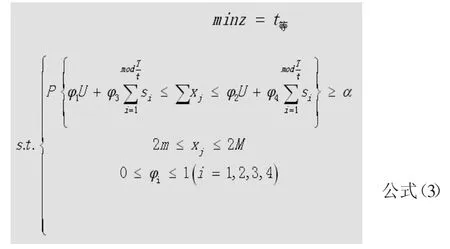
基于以上模型，以东部某海港第一季度为期90 d向某内陆方向到达集装箱数据为基础进行测算，其测算结果对比见表2。

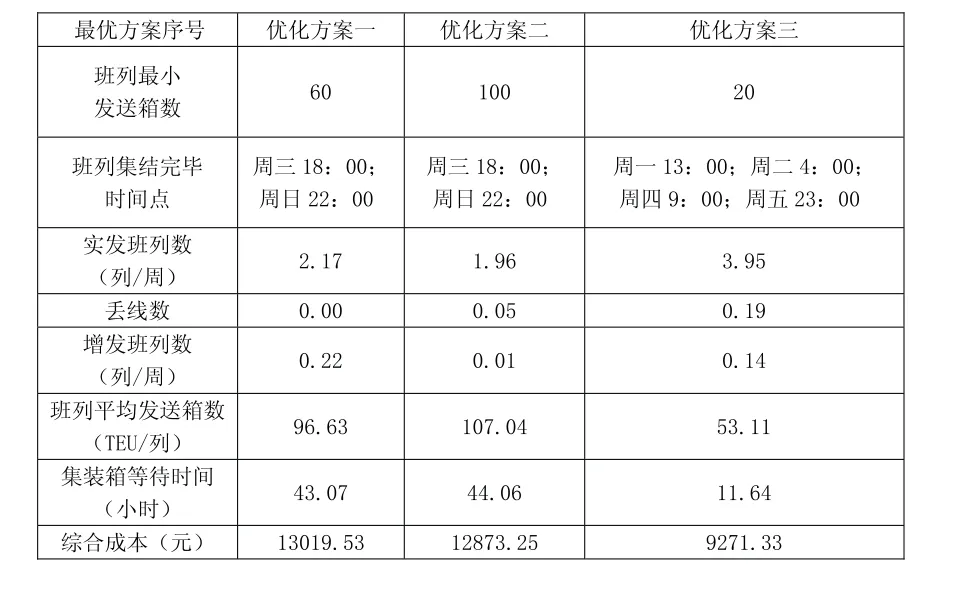
表2 优化结果对比

其中优化方案一与现行实际开行方案基本相似，而方案二提高最小发送箱数至100 TEU后，整体效果明显更优，而方案三通过较高的发送频次进一步降低等待时间和综合成本。由此可见，基于卷积理论的海铁联运集装箱班列开行优化方案可有效降低综合成本，提升服务质量。

4 结束语

本文提出可将卷积理论应用于海铁联运动态衔接可靠性分析中，基于卷积理论确定集结周期末在站剩余集装箱数，并在此基础上确定可靠性指标计算公式及建立以等待时间为目标函数的数学模型，最后通过实证研究确定满足海铁衔接可靠性要求的集装箱班列开行优化方案。但集装箱海铁联运的核心是一个复杂的动态衔接过程和一个多层面的系统问题，且卷积理论在运输问题方面的研究与应用比较少，所以针对本文中动态衔接可靠性指标运算的便捷性还有待进一步优化。