基于ABAQUS无限元的静-动力统一人工边界研究

王 飞， 宋志强， 刘昱杰， 王 建

(西安理工大学 水利水电学院， 陕西 西安 710048)

1 研究背景

国内外关于各种动力人工边界做了大量的研究工作，主要集中在局部人工边界和全局人工边界两大类上。常用的局部人工边界有透射边界[1]、黏性边界[2]、黏弹性边界[3-4]。全局人工边界的典型代表之一是无限元。1973年Ungless[5]首先提出了无限元思想，用以解决无限域模拟问题。Bettess等[6]根据整体坐标和局部坐标间的映射，提出了映射无限单元的概念，被称之为Bettess单元。1992年，Bettess[7]将已有的无限元研究成果进行归纳，出版了世界上首部无限元专著《Infinite Elements》。近年一些学者开始应用无限元研究结构-地基动力相互作用问题[8-10]。Kim[11]和Yun[12]创新了动力无限元公式，在频域和时域内研究了二维、三维层状土-结构的相互作用。许多学者研究经验表明，无限元与有限元协调性好，比边界元等其他数值方法求解无限域问题更具优势和实用性。戚玉亮等[13]对ABAQUS动力无限元人工边界进行了改进，但未讨论无限元对于静力人工边界以及静-动力统一人工边界的适用性。

对于一般符合小变形、线弹性的结构，可分别独立进行静力荷载和地震动力荷载作用效应分析，将二者叠加即为结构总作用效应。对于具有材料或接触非线性、强震作用下会发生大变形的结构叠加原理原则上是不适用的，必须进行静、动力统一分析，由此引出静、动力边界的转换或者统一问题。

文献[14]正确地给出了一种静-动力人工边界转换的方法，但此方法较为繁琐，且应用过程中容易由于未施加静力分析产生的节点约束反力，使得结构在动力零时刻不能保持平衡，导致计算结果失真。为了避免边界转换的繁琐，有些研究者开始进行静-动力边界的统一问题研究。

刘晶波等[15]提出了黏弹性静-动力统一人工边界，其物理概念清晰、计算公式明确，易于有限元实现。对于半无限空间自由表面在法向集中力和表面点波源振动作用下的静-动力问题分析结果表明，该静-动力统一边界在保证动力问题分析精度和稳定性的同时，兼顾了静力问题分析的精度，但该方法对于半无限自由表面切向集中力的静力数值解误差较大。

高峰等[14]用黏弹性静-动力统一人工边界分析半无限空间体应力，同样认为土体内部各点的横向应力与理论解之间存在较大偏差。在土木工程结构中，静力效应主要是结构自重引起的，因此这一不足不会影响黏弹性静-动力统一人工边界在该领域中的应用。而在水工结构中，除了结构自重，静水压力、淤沙压力等主要水平向荷载对结构的静力效应是不容忽视的。

为了既方便又相对准确地计算结构的静-动力综合效应，本文建立了基于ABAQUS无限元的静-动力统一人工边界。基于无限元在理论上满足无穷远处位移为零、波传播至无限远域衰减为零的条件[9]。推导了外源波动输入下无限元静-动力统一人工边界等效节点力计算公式，并基于Python语言编写了等效节点力计算与施加程序。该方法无需进行静、动力边界的转换和应力场、边界约束反力的导入，相比黏弹性静-动力统一边界条件，静力计算的精度更高，尤其适用于静力荷载为切向的情况，此外，基于无限元静-动力统一人工边界的有限元模型，地基有限域的模拟范围可以大幅缩小，而对静、动力计算的精度及综合效应并无较大影响，显著提高了计算效率。

2 基于ABAQUS无限元的外源波动输入研究

ABAQUS分析软件提供的无限元动力人工边界应用了Lysmer和Kuhlemeyer提出的黏性边界理论，区别在于阻尼器是内嵌均匀分布在ABAQUS提供的无限单元中。基于此，无限元人工边界下的自由场波动输入方式可参考黏性人工边界理论或黏弹性人工边界理论，即将地震波在边界处的自由场运动转换为作用于人工边界结点上的等效结点力进行施加如图1所示。

图1 黏弹性边界示意图

近些年来，黏弹性边界法的应用与改进较多，在模拟无限远域地基的辐射阻尼效应时，其精度和稳定性较黏性人工边界高[16-18]，故本文在参考部分黏弹性边界理论[3]的基础上推导出无限元动力边界法的地震动输入方式。

黏弹性边界法人工边界结点上的等效结点力公式为[16]：

(1)

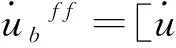
当公式(1)中的Kb=0时，便得到可应用于ABAQUS软件提供的动力无限元边界上地震动输入的等效结点力。Cb在不同人工边界面上有其特定的表达形式，当人工边界面外法线方向与x轴(如图1)平行时：

(2)

与y轴平行时：

(3)

与z轴平行时：

(4)

式中：CBN=cpρ、CBT=csρ，即内嵌均匀分布于动力无限单元内部的阻尼器的阻尼系数，与黏弹性人工边界的阻尼系数相同，因其计算与赋值由ABAQUS软件自动完成，与黏弹性人工边界法比较省去了大量的前处理工作；cp、cs分别为P波和S波波速，ρ为介质质量密度。

对于三维模型具体表达式如下：

(1)对于底面

(5)

式中：等效节点力上标代表节点所在人工边界面的外法线方向，规定与坐标轴正方向一致为正，反之为负；下标表示等效节点力分量的方向；H为边界底面到地表的距离，h为人工边界节点至底边界面的距离。

(2)对于x负向边界面

(6)

(3)对于x正向边界面

(7)

(4)对于y负向边界面

(8)

(5)对于y正向边界面

(9)

3 算例分析

为了比较本文提出的无限元静-动力统一边界在处理静-动力综合问题的优越性，本文对4种方法进行对比分析。为避免混淆，规定各种方法中人工边界的名称，并对各种人工边界做出简要说明，如表1。

表1 人工边界名称及施加方法

3.1 半无限空间体受表面法向均布静荷载和单位脉冲荷载联合作用

在半无限域中截取范围为-30.0 m≤x,y≤30.0 m、-50.0 m≤z≤0 m的模型模拟半无限空间体，坐标原点位于模型顶部中心点，如图2。模型介质质量密度ρ=1 000 kg/m3，弹性模量E=2.4×107Pa，泊松比ν=0.2。首先在模型表面中心区域作用矩形均布静荷载q=1×106Pa，矩形的边长为6.0 m，在模型的底面和侧面分别施加黏弹性动力人工边界(方法1)、黏弹性静-动力统一人工边界(方法2)和无限元静-动力统一人工边界(方法3)，如图3；接着在模型的底面垂直向上输入沿z向的单位脉冲P波以及沿x、y向的单位脉冲S波，其位移表达式见公式(10)，位移波形图见图4。由介质的弹性性质可得波速cp=163.30 m/s、cs=100.00 m/s。

另建立有限元-无限元耦合模型，其中内部离散有限域范围为-6.0 m≤x,y≤6.0 m，-50.0 m≤z≤0，在有限单元的外部包裹着无限单元，加载方式等同方法3，即方法4。采用方法1、方法2、方法3和方法4对该静-动综合力问题进行分析。计算时长为2.0 s，时间步长为0.01 s。

(10)

由弹性力学理论公式[19]和叠加原理，可得到模型顶部中心点O(0，0，0)、中部中心点B(0，0，-25)和底部中心点C(0，0，-50)的z向位移的理论解，图5～7给出了4种方法下点O、B和C的z向位移数值解。

由图5～7可知，模型在表面法向均布静荷载和从底面垂直向上输入的z向脉冲荷载的联合作用下，4种方法的z向位移与理论解的偏差都较小。图8给出了图5中点O在0.55s之后的位移时程曲线放大图，结果表明静-动力人工边界转换法和黏弹性统一人工边界法在外行波穿过边界时有小幅值的震荡，相比较而言，无限元统一人工边界法在边界处比较稳定。点B和点C的位移时程曲线也存在类似的现象。

3.2 半无限空间体受表面切向集中力和单位脉冲荷载联合作用

将3.1节中的矩形均布静力换为在坐标原点施加q=1×107N的切向集中力，其他不变。根据弹性力学的理论公式[20]和叠加原理，求得半无限空间体表面x轴方向上观测点D(2,0,0)、E(4,0,0)、F(6,0,0)的x向位移理论解。同样采用上述4种方法计算得到x轴方向上相应各点的x向位移数值解，如图9～11。

图9～11表明，模型在表面切向集中力和底面垂直向上输入的x、y向脉冲荷载联合作用下，无限元静-动力统一人工边界法的精度最高，即使是有限元-无限元耦合模型中的有限域范围缩减25倍后，数值精度并没有明显的降低。虽然在切向集中力附近，无限元静-动力统一人工边界法的x向位移数值解与理论解之间有一定误差，但是相比其他两种人工边界法，其x向位移数值解是最精确的，且距切向集中力施加点一定距离后，其x向位移数值解与理论解越接近。

当模型只受脉冲荷载作用时，黏弹性动力人工边界法、黏弹性静-动力统一人工边界法、无限元静-动力统一人工边界法的精度非常接近且较高，动力响应的误差对综合响应的误差贡献较小，说明综合响应的误差大小在很大程度上取决于静力效应的误差大小。

4 分析某混凝土重力坝的静-动力综合效应

取混凝土重力坝的某一标准坝段建立三维有限元模型。该坝段最大坝高H=100 m,坝底宽b1=66.5 m,坝顶宽b2=7.0 m,下游坝面坡度m=0.7,上游坝面为铅垂面。重力坝混凝土质量密度ρ=2 400 kg/m3,弹性模量E=24.0 GPa，泊松比ν=0.17；基岩质量密度ρ=2 600 kg/m3，弹性模量E=15.0 GPa，泊松比ν=0.25。上游正常蓄水位H0=95.0 m,下游正常蓄水位H1=9.7 m。规定坐标原点位于大坝上游面底部中心，x为顺水流向，指向下游为正，y向为垂直水流向，指向左岸为正，z向为竖直方向，指向上为正。

分析大坝在自重、上下游静水压力、扬压力以及地震作用下综合响应，其中动水压力在相应位置以附加质量的形式模拟。重力坝的两侧为自由边界，忽略相临坝段间的静、动力相互作用。

对于静力问题，在距结构一定远处地基的位移已很小，远域地基对结构的影响较小，可以忽略。通常情况，地基范围至少取1.0倍结构高度[21]，因此静-动力人工边界转换法(方法1)和黏弹性静-动力统一人工边界法(方法2)的有限元模型地基计算范围为：深度方向自建基面向下延伸1.0倍坝高，上、下游方向和左、右岸方向同样延伸1.0倍坝高，如图12。无限元静-动力统一人工边界法(方法3)的模型：在有限单元的(单元类型C3D8R)外围包裹一层无限单元(单元类型CIN3D8)，形成有限元-无限元耦合模型，以无限元模拟有限域地基外的无限域地基，如图13。

另建一有限元-无限元耦合模型，其中有限地基范围在深度、上下游和左右岸方向均取0.5倍坝高，地基范围缩小了7/8(方法4)。

根据工程实际情况以及NB 35047-2015《水电工程水工建筑物抗震设计规范》[22]中的标准设计反应谱人工拟合地震动加速度时程。重力坝所在地为I0类场地，场地特征周期Ts=0.2s,标准设计反应谱最大值得代表值βmax=2.0，水平地震动峰值加速度PGA=0.1g,竖向地震动峰值加速度取水平向的2/3，加速度总时长t=20 s，时间步长为0.01 s。地基-大坝体系采用Rayleigh阻尼模型，按结构体系的前两阶自振频率(f1=1.614、f2=2.521)确定阻尼常数，两阶阻尼比均为0.1，阻尼常数ɑ0、ɑ1分别为1.259和0.0077。利用SeismoSignal或Matlab等软件通过数值积分求得各向速度、位移时程，即可将地震动输入转换为等效节点力加载到有限元模型和有限元-无限元耦合边界面节点上。

图14和15 给出了不同边界法上游坝面坝顶中心点的x向和z向相对静动力综合位移时程，位移参考点为坐标原点，可见不同的边界法对坝顶位置的顺河向和竖向静动综合位移影响较小。图16和17给出了上游坝面不同高度处的x向和z向相对位移最大值，经过归一化可以看出，3种不同边界法的z向最大相对位移的差别沿坝高基本不变，说明3种边界法对于坝体的竖向静动力综合位移的计算精度是相近的。3种边界法的x向最大相对位移的差别随着坝高的增加逐渐减小，即对于水平向静动综合位移，3种边界法的精度在坝高度较低的位置差别较大。根据以上半无限体的分析结论，3种边界法的动力位移精度是相近的，从图18同样可以看出，3种边界法的静动力综合效应的波型相似，只是均值水平上相差一个固定值，即由静力效应引起的差别。造成这种结果的原因是前2种边界对于静力荷载为切向时的误差较大。而无限元边界方法则克服了这一缺点。可见，对于常常承受水平切向荷载的水工结构来说，水平向位移的精度是至关重要的，因此，对于水工结构的静动力综合问题，本文提出的无限元方法是适合的，另外2种方法较为繁琐，精度也不理想，并且将无限元静-动力统一人工边界法的地基计算范围缩小了7/8后，x向相对位移的误差仍然小于黏弹性静-动力统一人工边界法和静-动力人工边界转换法。

图2有限元模型图3有限元-无限元耦合模型

图4入射位移波波形图图5模型顶部O点的z向位移解

图6模型中部B点的z向位移解图7模型底部C点z向位移解

图8 O点0.55s之后z向位移解图9模型顶部D点x向位移解

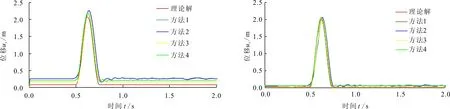
图10模型顶部E点x向位移解图11模型顶部F点x向位移解

图12有限元模型图13有限元-无限元耦合模型

图14坝顶x方向相对位移时程曲线图15坝顶z向相对位移时程曲线

图16不同坝高位置归一化x向相对位移图17不同坝高位置归一化z向相对位移

图18 坝高h=6.0 m处x向相对位移时程曲线

5 结 论

本文根据黏弹性动力边界理论，推导出有限元-无限元耦合界面上适用于外源波动输入的等效节点力计算公式，基于Python语言，编制了等效节点力计算与施加为一体的程序，从而建立了基于ABAQUS无限元的静-动力统一人工边界。这种边界在计算结构的综合效应时，不需要进行静、动力边界转换、应力场的导入以及节点约束反力的施加。通过对算例和实际工程的分析得出以下结论：

(1)ABAQUS无限元静-动力统一人工边界法实现相对简单，其计算精度较静、动力人工边界转换法和黏弹性静-动力统一人工边界法的精度要高，尤其当静力作用方向为水平向时，其精度优势能够得到突显。应用ABAQUS无限元静-动力统一人工边界条件分析重力坝-地基体系受静-动力联合作用的地震响应，验证了该边界对水工结构静-动力分析的适用性。

(2)有限元-无限元耦合模型中的有限域地基范围被大幅度缩减后，ABAQUS无限元静-动力统一人工边界法的计算精度仍然较高。表明该方法在提高计算效率的同时仍然能够保持较高的精度，这对于大型非线性问题分析有良好的应用前景。