具有通过流动的倾斜腔体的对流特性
2019-01-25宁利中宁碧波田伟利渠亚伟
刘 爽, 宁利中, 宁碧波, 田伟利, 渠亚伟
(1.西安理工大学 省部共建西北旱区生态水利国家重点实验室, 陕西 西安 710048;2.嘉兴学院 建筑工程学院, 浙江 嘉兴 314001; 3.上海大学 建筑系, 上海 200444)
1 研究背景
现实生活中的对流实例普遍存在,小到刮风,大到热作用下大气对流导致的突发性降雨、软层流在地壳中的运动等。1900年Bénard在盛有薄流体层的水平金属板底部加热实验中首次发现了热对流运动现象。1916年英国科学家Rayleigh等引进小扰动理论思想,对这类底部加热的流体展开了深入研究[1],发现瑞利数Ra是控制流体稳定性的主要因素,这一发现为以后热对流的理论研究奠定了基础,并由此命名为Rayleigh-Benard(简称“RB对流”)。
就二维平面来说,RB对流系统就是在一个完整密闭的矩形腔体内,当上壁面处于恒温状态,给下壁面进行加热,底部流体则会因加热膨胀、密度减小而上升,接触到其他流体时温度降低而密度增大。当底部流体温度到达一定值而密度足够小时,则产生冷热流体互相交换的规则的滚动斑图现象[2]。RB对流具有理论和实际意义[3-7],因其简单且易控制等特性为流体力学及其他相近学科的研究奠定了基础;并可利用Fluent软件对其进行二维或三维数值模拟[8-15],这也为其他非线性问题指明了一个可行性的研究方向;更为重要的是RB对流应用广泛涉及众多领域,例如,太阳辐射使地表升温通过对流将热量传递给空气;海洋受到温度和盐度双重影响而形成热盐对流;水库、海洋、湖泊中的热对流;不同类异型强化换热管的应用[16-17];地幔中以自放射性元素衰败为加热体并以地球板块为模型形成对流[18],使得地壳运动,从而产生一系列地形结构的变化;还可以帮助人们解决金属固化、污染物扩散、核反应堆冷却、化学气体的沉淀与干燥、太阳能利用等一些实际应用的问题等等。
基于水平来流对混合流体时空特性的影响、不同水平来流强度导致时间依赖的动力学行为以及倾斜腔体均热条件下的对流特性等诸多研究[19-20],本文主要研究的是在矩形腔体中,倾斜角度一定且均匀加热的条件下,通过改变通过流动强度和相对瑞利数r进行二维数值模拟,以获取腔体内对流结构及其相关特性的变化规律。
2 数学模型
2.1 模型的建立
本文建立的模型是倾斜角为10°时的矩形腔体(如图1所示,半圆中的箭头表示从左侧进口进入的通过流动;矩形中的圆圈表示温差引起的对流圈),在长高比Γ=20的窄长腔体中充满普朗特数Pr=6.99的水。在左侧面有通过流动,下壁面加热的条件下,由于通过流动强度与温差的共同作用,使得腔体内流体产生丰富的对流斑图。
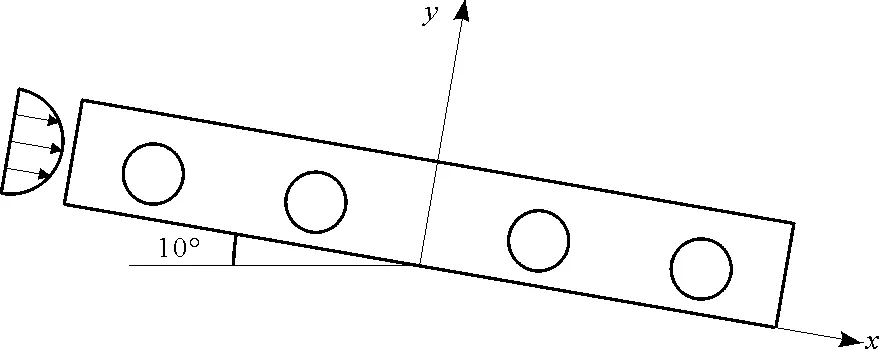
图1 对流模型
2.2 基本方程
就封闭腔内而言,为方便处理受温差影响的浮力项,在对其进行自然对流传热数值计算时,通常采用Boussinesq假设[21],即只考虑浮力项中温度足够小时,引起的密度变化。描述该问题的方程组[22]可表示为:
(1)
(2)
(3)
(4)
式中:peff=p+ρ0gycosθ-ρ0gxsinθ;u,w分别为平行和垂直于腔体长度方向的速度,m/s;T为温度场,K;ρ为密度,kg/m3;p为压强,Pa;g为重力加速度,m/s2;ν为运动黏性系数,m2/s;α为体积膨胀系数,K-1;κ为热扩散系数,m2/s;t为时间,s;θ为倾斜角度,(°);下标0表示传导状态下的各物理量初始值。
2.3 边界和初始条件
在均匀加热的条件下,为方便求解方程组,需给出合理的速度场、温度场的边界及初始条件。
当x=0时,有通过流动的左侧入口边界条件为:
(5)
w=0
(6)
(7)
当x=Γ时,右侧出口边界条件为自由出流。
当y=0时:
u=w=0
(8)
(9)
当y=d时:
u=w=0
(10)
(11)
式中:ΔT为腔体上、下面温差;d为腔体高度;Γ为腔体长高比;umax为通过流动的流速最大值;T0为平均温度,取其平均值为293.15K,初始速度为u=w=0。
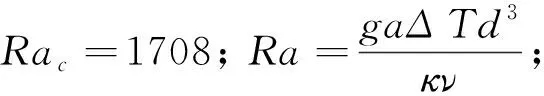
2.4 数值计算
基于文献[23]对网格划分的误差分析,本文采用Gambit对Γ=20的矩形腔体进行20×400的均匀交叉网格划分,对非定场流采用一阶隐式,速度均用绝对速度,用有限容积法对流体力学方程组进行离散,对速度-压力耦合方程用Simple算法求解。
本文主要通过改变流动强度和相对瑞利数来分析其对腔体内的对流斑图结构及相关物理量的影响。
3 具有通过流动的倾斜腔体的对流特性
3.1 对流斑图的演化特性
3.1.1 对流斑图随相对瑞利数的变化 在Γ=20的矩形腔体中,选用Pr=6.99的流体,倾斜角度为10°,在左侧入口有通过流动时,给下壁面加热,当雷诺数Re=0.5,相对瑞利数分别为r=2、3、6、9时,得到不同结构的对流斑图,如图2所示,图中横坐标表示腔体长度,纵坐标为腔体高度。由图2可知,当相对瑞利数r=2、3时,该流体只存在单个对流圈与通过流动的混合;但随着相对瑞利数r的增大,腔体内出现对多个对流圈与通过流动混合现象,对流强度也随之明显变大;这是由于温差逐渐加大,使得热作用逐渐增强而产生的。
3.1.2 对流斑图随雷诺数的变化 相对瑞利数一定时,分析不同雷诺数下的对流结构变化,如图3所示,即在r=9,雷诺数分别为Re=0.5、2.5、5、7.5时的对流斑图。由图3可知当雷诺数较小(即Re=0.5)时,腔体内混有多个对流圈与通过流动,且热作用占据主导地位,通过流动强度较弱;随着雷诺数的增大,当其达到一定值(Re=2.5)后,腔体内出现明显的分区现象,靠近上下壁面的区域为对流区,中间为通过流动区域,此时通过流动与热作用共同作用且均得到了充分发展而达到平衡;雷诺数逐渐增大,滚动圈随之逐渐减小,与之相反,通过流动强度则不断增大直至完全稳定状态。当雷诺数继续增大至Re=7.5时,流体中出现局部行波的现象,上游区域为通过流动,下游区域为通过流动与热作用的耦合。

图2Re=0.5时对流斑图随不同相对瑞利数r的变化图3r=9时对流斑图随不同雷诺数Re的变化
3.2 最大垂直流速特性
3.2.1 雷诺数对最大垂直流速的影响 图4所示为r=6、雷诺数分别为Re=0.5、3、5时,最大垂直流速wmax随时间的分布规律。由图4可知,随着时间的推移,最大垂直流速wmax的变化规律可分为3个阶段,即发展阶段、过渡调整阶段和稳定阶段(稳定周期阶段)。当雷诺数较小时,由发展阶段向过渡调整阶段变化时,wmax随时间的成长速率较小,过渡调整阶段至稳定阶段耗时较长,且呈不规则震荡变化,wmax稳定值也较小。随着雷诺数的不断增大,wmax随时间的成长速率逐渐变大,过渡调整阶段至稳定阶段所需时间相应减少,震荡趋于规律化,最大垂直流速wmax均一次性下降到稳定值,且wmax稳定值也随之增加。
3.2.2 相对瑞利数对最大垂直流速的影响 图5为Re=4、相对瑞利数分别为r=3、6、9时,最大垂直流速wmax随时间的变化规律。由图5可知,当雷诺数一定而相对瑞利数较小时,其最大垂直流速wmax直接由发展阶段向稳定阶段转变,快速达到稳定状态,且wmax稳定值也较小;这是由于温差较小时,通过流动强度抑制了热作用而占据主导地位。随着相对瑞利数的增大,wmax随时间的变化阶段完整化,当相对瑞利数较大时,其对流速的影响与雷诺数对流速影响规律几乎一致;不同的是当相对瑞利数达到一定值后,其向过渡调整阶段转变时成长速率较大,在该阶段其最大垂直流速wmax变化幅度显著,历时较短;随后向稳定周期变化阶段过渡时,最大垂直流速wmax分两层次下降,最后呈现为周期变化。
3.3 下壁面努塞尔数变化规律
3.3.1 雷诺数对努塞尔数的影响 图6所示为r=6时、雷诺数分别为Re=0.5、3、5条件下努塞尔数Nu随时间的变化规律。由图6可知,当相对瑞利数一定时,下壁面努塞尔数Nu均是由最大初始值开始呈对数下降到一定值,然后再缓慢减小至稳定值后几乎趋于一条直线。图7所示为r=3、Re=4时,Nu与时间的拟合关系图,呈对数式关系:Nu=-18lnt+66.706。随着雷诺数的逐渐增大,最大初始值没有变化,努塞尔数Nu的下降速率逐渐变大,达到稳定状态所需的时间先增大后减小(详见表1),其稳定值相应增加,但其增加的数值相差不大,最大不超过3.8%(如表1所示)。由此可以得出:当通过流动强度与热作用相互作用,相对瑞利数一定,雷诺数Re虽然对努塞尔数Nu有一定影响,但其影响能力有限。

图4r=6时不同雷诺数下最大垂直流速wmax随时间的变化图5Re=4时不同相对瑞利数下最大垂直流速wmax随时间的变化

图6r=6时不同雷诺数下努塞尔数Nu随时间的变化图7r=3、Re=4时努塞尔数Nu随时间的变化
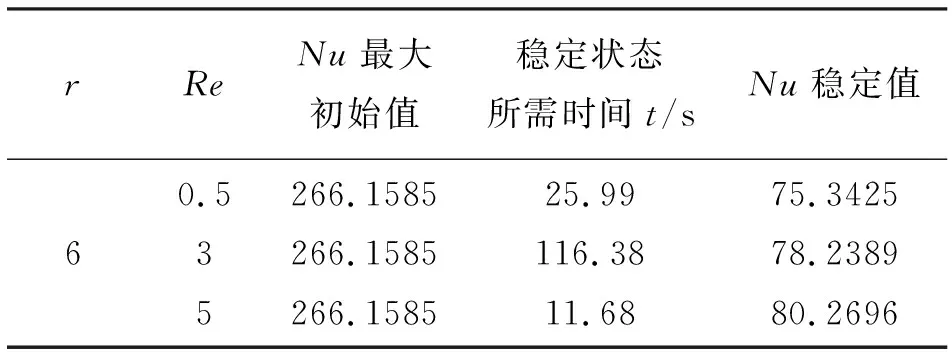
表1 Nu的相关参数随Re的变化
3.3.2 相对瑞利数对努塞尔数的影响 图8所示为Re=4时、相对瑞利数下分别为r=3、6、9条件下努塞尔数Nu随时间的变化规律。由图8可知,当雷诺数一定时,不同相对瑞利数下努塞尔数Nu随时间的变化规律基本相同。但随着相对瑞利数的不断增大,由最大初始值减小至稳定值的时间反而增加,其相应增加的稳定值相差很大,甚至成倍数增大,详见表2。这充分说明了当通过流动强度与热作用共同作用时,雷诺数一定,相对瑞利数r对努塞尔数Nu影响显著。
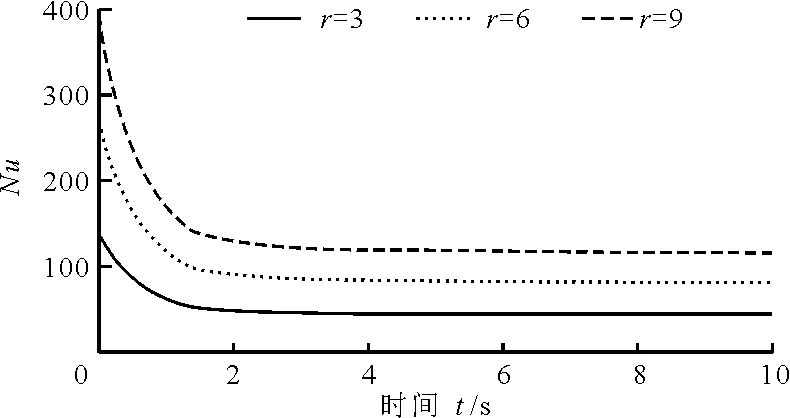
图8 Re=4时不同相对瑞利数下努塞尔数Nu随时间的变化
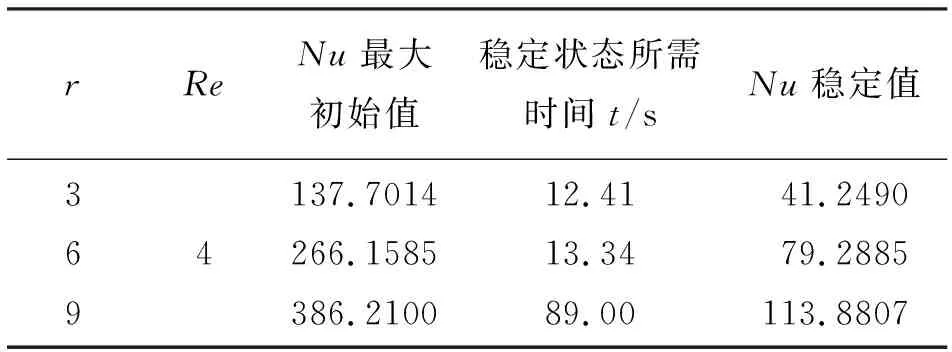
rReNu最大初始值稳定状态所需时间t/sNu稳定值3694137.7014266.1585386.210012.4113.3489.0041.249079.2885113.8807
4 结 论
本文在倾斜角度为10°且Γ=20的矩形腔体中,选用Pr=6.99的流体,通过改变流动强度和相对瑞利数来分析其对腔体内的对流斑图结构及其相关特征物理量的影响。得到的结论如下:
(1)相对瑞利数一定,随着雷诺数的不断增大,对流斑图变化明显,由通过流动与单个对流圈的混合演变成多个对流圈与之混合;最大垂直流速wmax均历经发展、过渡调整和稳定3个阶段,其稳定值相应增加,但其增量较小;努塞尔数Nu变化规律相同,均由最大初始值呈对数下降,而后达到稳定,其稳定值也相应增加,但增加值也不大。由此可知,当通过流动与热作用共同作用时,雷诺数Re对对流斑图影响较大,但对最大垂直流速wmax及努塞尔数Nu影响能力有限。
(2)雷诺数一定,随着相对瑞利数r的增加,对流斑图呈现多种变化形态,由最初的通过流动与多个対流圈的混合逐渐达到充分发展的平衡状态,而后出现局部行波;最大垂直流速wmax的变化趋势及历经阶段也各不相同,其稳定值增加幅度较大;努塞尔数Nu变化规律不变,但其最大初始值与稳定值几乎成倍增加。所以,当通过流动强度与热作用共同作用时,相对瑞利数r对对流斑图、最大垂直流速wmax及努塞尔数Nu影响显著。
