基于改进云模型的水利PPP项目风险分担研究
2019-01-25袁宏川张伟龙游佳成
袁宏川, 张伟龙, 游佳成
(三峡大学 水利与环境学院, 湖北 宜昌 443002)
1 研究背景
水利工程是国家重要的基础设施建设,2017年,政府颁布《政府和社会资本合作建设重大水利工程操作指南(试行)》,规范了水利PPP(Public Private Partnership)项目运作,进一步推进了PPP模式在我国水利行业的应用与发展。由于水利PPP项目投入资金大、合作周期长、作业条件差、利益方众多,导致政府和社会资本双方在实施过程中存在诸多风险。如何整合政府和社会资本的资源优势实现对风险的合理分担将显得至关重要,这关系到项目的安全、参与者的积极性及方案的合理设计,因此对水利工程PPP项目的风险分担问题进行研究具有重要意义[1]。
目前,国内学者应用层次分析法和合作博弈理论[2]、熵权法和模糊综合理论[3]、粗糙集理论[4]、云模型[5]和效用理论[6]等方法对PPP项目进行了风险分担问题的研究,取得了一定的研究成果。但现有研究方法未综合考虑风险分担决策的模糊性和随机性、行为认知偏差及自身的有限理性对风险分担方案决策的影响;同时,目前结合水利工程的PPP项目风险分担研究也不够完善。
水利PPP项目的风险分担指标具有突发性及演变性等特征,存在较强的模糊性和随机性等问题,而基于定性描述与定量数值间进行相互转换的云模型[7-8],能够很好地解决该问题;同时,前景理论[9-10]能够避免水利PPP项目评价专家在复杂多变的决策环境下做出主观判断,能够有效反映其行为模式。
鉴于此,全文以水利PPP项目为切入点,充分考虑决策者的心理效用和不确定性的信息,建立基于改进云模型的风险分担方法,最后以案例验证了该方法的有效性。
2 风险分担决策指标体系的构建
水利工程规模大、地质条件复杂多变、作业人员和机械密集、横向和纵向交叉作业多、协同作业困难,这些因素导致水利工程在投资开发中会诱发较多的风险[11]。PPP项目具有投入资金大、实施周期长、合作方众多、统筹管理难度大等特征。因此,水利PPP项目投资主体在利益分配、契约合作协议、个体行为差异等方面存在较多的不确定因素。
鉴于此,综合参考文献[12-14],并结合水利PPP项目施工现场调研结果,从政治、法律、自然、投资、建设、运营6个方面建立水利PPP项目风险分担决策指标体系,如图1所示。
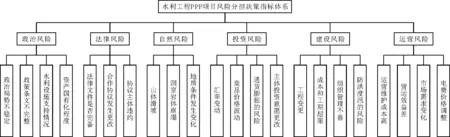
图1 水利工程PPP项目风险分担决策指标体系
3 风险分担方案决策方法的构建
3.1 问题描述
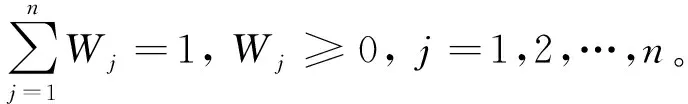
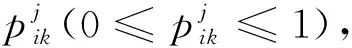
3.2 指标评语云的构建
通过水利工程领域PPP项目库专家制定有效论域U=[Xmin,Xmax],根据云模型生成算法[15],生成5朵云与相应决策指标评语一一对应。针对前文提出的5种风险分担决策指标评语,参考水利PPP项目库专家设置的有效论域U=[0,1],按照上述云模型生成算法生成的5朵云分别对应{S1,S2,S3,S4,S5},具体参数见表1。
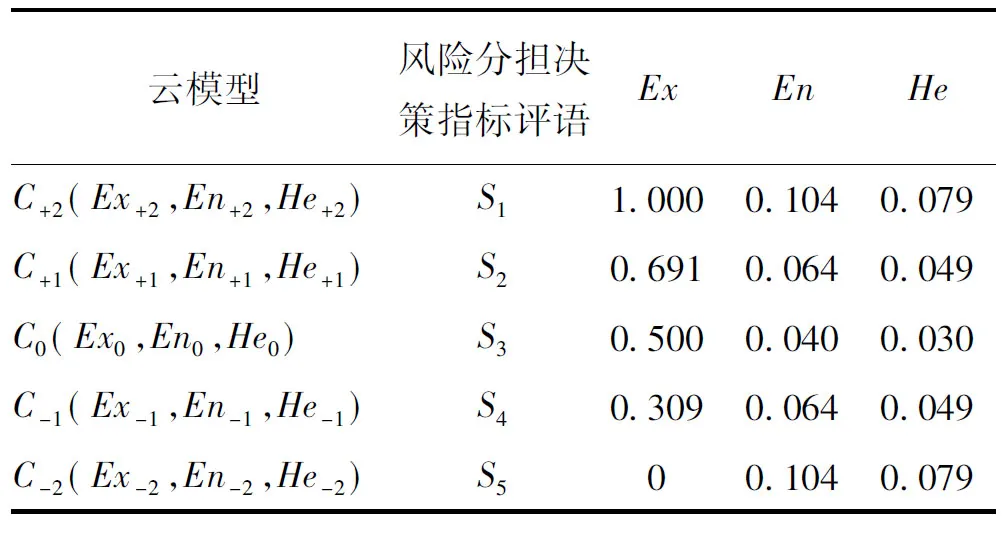
表1 风险分担决策指标评语云
3.3 指标云前景价值的计算
3.3.1 云理论定义 两朵云C1(Ex1,En1,He1)和C2(Ex2,En2,He2),根据 “3En”原则,计算两朵云之间的距离[15]D(C1,C2)为:
(1)
其中:
d(C1,C2)=
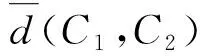
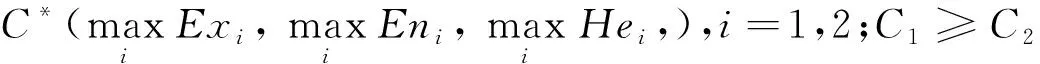
(2)
式中:D(C*,C1)和D(C*,C2)为正态理想云C*与两朵云C1和C2之间的云距离。如果云可能度P(C1≥C2) ≥0.5,则C1≥C2,否则,C1≤C2。
3.3.2 云前景价值函数 将云模型引入前景理论,用云模型表示风险分担决策指标评语,结合云距离和云可能度定义,以云C1和C2为例,其中C2为心理参照点,得到C1的价值函数[15]v(C1)为:
(3)
式中:α和β(0≤α,β≤1)为决策者在不确定性条件下面对损益值的感知程度,决策者对损益值的感知程度与α和β大小成正相关;λ为风险规避系数,风险的敏感度随其增大而增大。
在面临复杂多变的风险时,决策者凭借主观感知作出判断,会规避风险损失。因此,对于风险偏好心理参考点的选取显得至关重要。根据投资人的心理偏好差异选择心理参考点,通过下式得到各风险分担决策指标的云前景值Vij:
(4)

(5)
(6)

3.4 计算指标最优权重
考虑决策者对风险的心理承受能力及预期收益,用离差最大化方法建立线性优化模型,即:
(7)
式中:H为不完全确定的风险系数空间。
3.5 方案综合云前景值的计算
计算各方案的综合云前景值,按照由大到小的方式排序,择优选择方案。
(8)
4 案例分析
某水利工程PPP项目是一座以发电为主,兼顾防洪、航运、灌溉等综合效益的枢纽工程,设计总库容1.187×1010m3,电站总装机容量3.6×105kW。总投资99.22×108元,其中政府出资40.17×108元,社会资本组成的联合体出资39.16×108元,其余资金通过向金融机构借贷方式筹集。
双方在长时间的合同谈判中,得出3套风险分担决策方案,即方案集A={A1,A2,A3},根据风险指标集Z={Z1,Z2,…,Z22}确定最佳备选方案。投资者充分考虑该项目的战略价值、功能定位、预期收益、可融资性、风险管理要求并参照以往水利工程风险偏好选择,结合该项目施工现场调研结果,得到式(7)对应的不完全确定的风险系数空间H。根据此前确定的风险分担评语,决策者对各方案指标的评价数据见表2,由于篇幅有限,在此仅列举3个风险分担方案的前3个指标的评语。
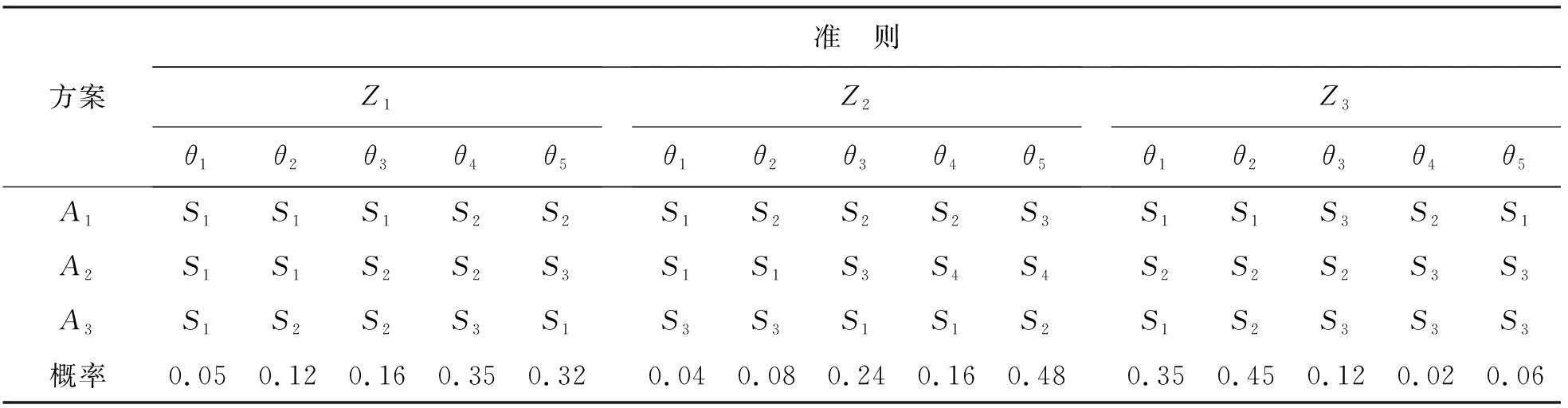
表2 风险分担方案语言评价表
(1)在各自然状态下,针对不同的风险组合方案,由于决策者对风险的感知存在差异,从而产生不同的心理参考点。以方案A1的前3个风险分担决策指标为例,根据投资者的风险偏好心理,得到前3个风险分担决策指标的心理参考点分别为C1={0.5,0.06,0.04},C2={0.7,0.05,0.04},C3= {0.6,0.072,0.04},根据公式(5)和(6)得到价值函数结果和权重函数结果,各系数为:α=β=0.88,λ=2.25,γ=0.61,δ=0.69[15]。通过计算得到各方案前3个风险分担决策指标的云前景值,如表3所示。
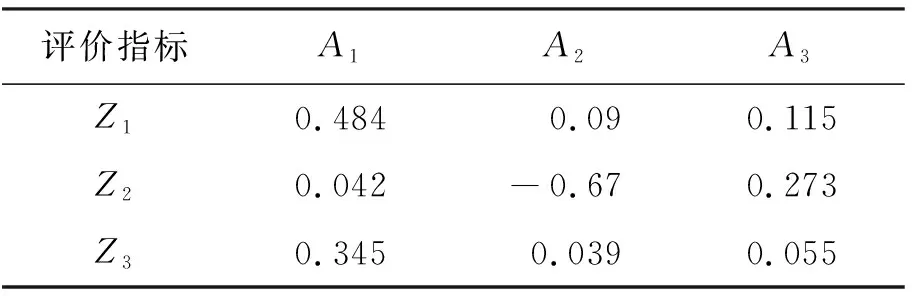
表3 各方案部分风险分担决策指标云前景值
(2)根据离差最大化方法及不完全确定的风险系数空间H,通过公式(8)得到最优化模型:
maxV(W)=0.419W1+1.655W2+0.322W3+0.311W4+0.588W5+0.773W6+0.797W7+
1.137W8+0.291W9+0.908W10+0.266W11+
0.283W12+0.809W13+0.949W14+1.755W15+
0.661W16+0.578W17+0.674W18+0.225W19+
0.408W20+0.53W21+1.299W22
s.t. 0.15≤W1≤0.2,0.049≤W2≤0.052,
0.125≤W3≤0.14,0.028≤W4≤0.031,0.043≤W5≤0.045,0.046≤W6≤0.048,0.115≤W7≤0.12,0.026≤W8≤0.027
W1>W3>W7>W14>W2>W6>W5>W13>W11>W12>W4>W8>W18>W19>W17>W9>W15>W16>W10>W20>W21>W22
通过Matlab软件遗传算法(genetic algorithm,GA)工具箱模块,首先将自变量的约束条件导入,程序会自动模拟生成一组向量;然后,代入目标函数得到一个最大值;最后,如果最大值有提升空间,程序将自动迭代直至获得最优解,据此可计算出最优模型的权重系数向量:
W*={0.2,0.049,0.14,0.03,0.045,0.048,0.12,0.027,0.019,0.019,0.03,0.031,0.034,0.049,0.02,0.019,0.019,0.019,0.02,0.02}。
(3)根据式(6)计算出3个方案的综合云前景值:V1=-0.054,V2=-0.271,V3=-0.168,得到A1>A3>A2,故A1为最优方案。
该方案最终从3个备选方案中选择方案A1为最优方案,进一步分析,将基于云模型和前景理论的方案决策方法与现有方法相比,从指标评语云模型的生成到各指标云前景值的确定以及各指标最优权重的计算都充分考虑了模糊性和随机性问题;同时,本研究充分考虑人获取信息和处理信息存在的局限性,现有方法所得决策结果无法反映这些问题。在整个项目方案实施中,采用方案A1对该项目的风险进行分担,严格满足由风险控制力强的一方承担、考虑风险上限及风险与收益相对应等原则,最终有效控制了风险,达到了预期的分担效果。
5 结论与讨论
(1)综合应用云模型和前景理论,结合人的行为和认知习惯,从指标评语云模型的生成到各指标云前景值的确定以及各指标最优权重的计算均充分考虑决策信息的模糊性和随机性,保证了决策结果的客观、有效,符合实际结果。
(2)案例分析结果表明,该决策方法与现有方法相比,充分考虑人获取信息和处理信息存在的局限性,为后续确定项目收费定价机制、投融资方案及建设运营移交方案提供了有力的支持。
(3)综合云前景值的准确性依赖于投资者心理参考点的选取,而心理参考点的选取往往依靠决策者的主观感受和以往经验,存在差异性,如何科学合理的选取心理参考点将是以后研究的重点。
