基底支撑刚度梯度变化对石墨烯层间摩擦力的影响∗
2019-01-25董赟段早琦陶毅GueyeBirahima张艳陈云飞
董赟 段早琦 陶毅 Gueye Birahima 张艳 陈云飞†
1)(东南大学机械工程学院,江苏省微纳生物医疗器械设计与制造重点实验室,南京 211189)
2)(兰州理工大学机电工程学院,兰州 730050)
(2018年10月26日收到;2018年11月22日收到修改稿)
基于纳米摩擦能耗理论,利用分子动力学方法建立了公度接触下支撑刚度梯度变化的石墨烯层间摩擦力模型,分析了基底质心刚度和支撑刚度梯度变化对基底和薄片各接触区摩擦能耗的贡献.结果表明:软边界区始终贡献驱动力;硬边界区贡献的摩擦力最大,且随着支撑刚度的增大,硬边界区对总摩擦的贡献比也越高.各接触区的摩擦力是薄片和基底之间的褶皱势和接触区产生的法向变形差两部分的共同作用.前者是公度接触下阻碍滑移的界面势垒和刚度梯度方向上不同刚度支撑原子热振动引起的势梯度;后者是接触边界过渡区两侧原子的非对称变形和自由度约束突变引起的非平衡边界势垒相耦合的结果.本文对研究公度接触下刚度梯度支撑的纳米器件的相对运动规律有指导意义.
1 引 言
当两个接触的物体发生相对运动或具有相对运动趋势时,阻碍其相对运动的力称为摩擦力,接触面之间的这种现象或特性叫摩擦[1,2].摩擦本质上是接触表面原子相互作用下的不可逆能量耗散,涉及复杂的非平衡态热力学过程[3-5].从组成物质的原子层面分析,光滑接触变成了众多粗糙峰接触,宏观应用的连续介质接触理论不再适用于微观离散接触模型[2,6,7].石墨烯是一种具有原子级厚度的二维碳材料,因其特有的大比表面积结构,被认为是理想的摩擦力研究材料[8-10].同时,由于其具有优异的力学、热学、电学和光学等性质,人们认为它将有可能取代硅,开启新的“碳时代”.当前石墨烯基器件的应用研究迅速发展,在纳米晶体管、透明导电薄膜、高灵敏度传感器、微/纳机电系统等方面都取得了实质性的进展[11-13].在一些纳米器件中,石墨烯层间的相对运动诱导机械功[10,14],同时由于其层间较弱的范德瓦耳斯力和较强的层内共价键作用,多层石墨烯可以作为理想的固体润滑剂[15-17].于是,以石墨烯为研究对象,从原子级的长度尺度和声子级的时间尺度观察摩擦现象,探究其规律,理清相关机理,构筑纳米摩擦理论已成为当前最受关注的纳米摩擦学研究内容[18].
基于纳尺度驱动和能量转换的重要性,人们对纳米器件定向运动的研究引起了广泛关注.Bailey等[19]在非手性外碳纳米管两端施加直流电压产生电流,使手性内碳纳米管形成旋转扭矩以克服内外管间的摩擦力做旋转运动.Guo等[20]通过实验对一双壁碳纳米管的内管两端施加电流后发现,较短的外管会做定向平动或转动,即使改变了外加电流方向,外管的运动状态也不会改变,作者将此现象归因于初始电流使内管沿轴向方向产生的非均匀性热流形成的温度梯度,造成内外管接触区的范德瓦耳斯势能差以及连接边界过渡处热振动幅值差的共同作用驱使外管运动.Somada等[21]利用透射电子显微镜发现了一“胶囊”型碳纳米管在长纳米管内做往复直线运动,并用分子动力学证明了驱动力由两部分造成,分别是外管端部“壁帽”和“胶囊”之间的范德瓦耳斯作用吸收了系统能量造成外管两端部形成“能量谷”以及热振动导致的纳米管轴向波状变形.Shiomi和Maruyama[22]以及Coluci和Hernandez[23]也分别通过水分子簇和富勒烯在碳纳米管中的定向运动证实了驱动力是由温度梯度引起的.不同于以往在碳管或基底两端持续施加外激励以保持恒定的驱动力,Chang等[24]将锯齿型(zigzag)石墨烯薄片放置在刚度梯度支撑的扶手椅型(armchair)石墨烯基底上(非公度接触),发现薄片会自发地从刚度较小区域向较大区域滑动,说明系统内部自身材料属性的差异会诱导刚度梯度方向的驱动力.当器件滑过两个不同约束基底或两种材质界面时,由于材料弹性模量的不同导致支撑体在滑动方向上形成刚度梯度,并且公度接触时界面之间的范德瓦耳斯势能小,接触稳定,两摩擦副界面通常以公度方式接触[25-27].所以,结合刚度梯度诱发的驱动力和公度接触下界面褶皱势引起的阻碍力研究纳米器件的滑移行为非常重要.而将石墨烯层间公度接触和基底支撑刚度梯度变化相结合的相对运动,国内外学者鲜有研究.因此,研究公度接触下刚度梯度对石墨烯层间摩擦力的影响,具有重要的科学和现实意义.
本文基于原子尺度摩擦能耗机理,利用分子动力学方法建立了刚度梯度支撑的石墨烯摩擦模型,研究了公度接触下各实际接触区和边界过渡区对摩擦力的贡献,揭示了石墨烯薄片和基底之间的褶皱势和各接触区之间的法向变形差的耦合作用是产生摩擦力的直接原因,为探索纳米摩擦能耗机理提供理论指导.
2 分子动力学模型
本文建立的模型系统包括模拟原子力显微镜(atomic force microscope,AFM)探针针尖吸附的一方形石墨烯薄片和刚度梯度变化支撑的单层石墨烯基底,如图1所示.利用法向刚度沿X方向线性递增的“弹簧床”将支撑体和基底石墨烯的每个原子相连接.为了模拟探针悬臂,将石墨烯薄片质心用弹簧连接于沿X方向以恒速3 m/s滑动的外部一虚拟原子(相当于悬臂梁),薄片和基底在滑动方向均为锯齿型(即公度接触)且在Y方向等宽,并以A-B方式堆垛[28].石墨烯基底尺寸为21.5 nm×6.7 nm(5632个原子),薄片尺寸为6.7 nm×6.7 nm(1792个原子),晶格常数为0.142 nm,薄片质心初始位置位于离基底质心偏软区域1.87 nm处.基底沿X方向两端3列原子为支撑边界,约束其除Z方向平动外的所有自由度,紧邻支撑边界的3列原子为调温边,约束薄片沿Y方向的平动和绕Z轴的转动,系统的Y方向设置成周期性边界条件.同层原子之间的作用势采用Terso ff-Brenner势[29],薄片和基底之间的作用势采用耦合强度较弱的Lennard-Jones势,势阱常数为3.73×10-3eV,平衡常数为0.34 nm,截断半径为0.884 nm[30].系统采用NVT系综(粒子数,体积以及温度均保持恒定),并通过Langevin调温法调节温度到300 K,时间步长为0.5 fs,滑移总时长为1.25 ns.所有的模拟都是通过LAMMPS软件包[31]实现并在1.5 ns内完成.
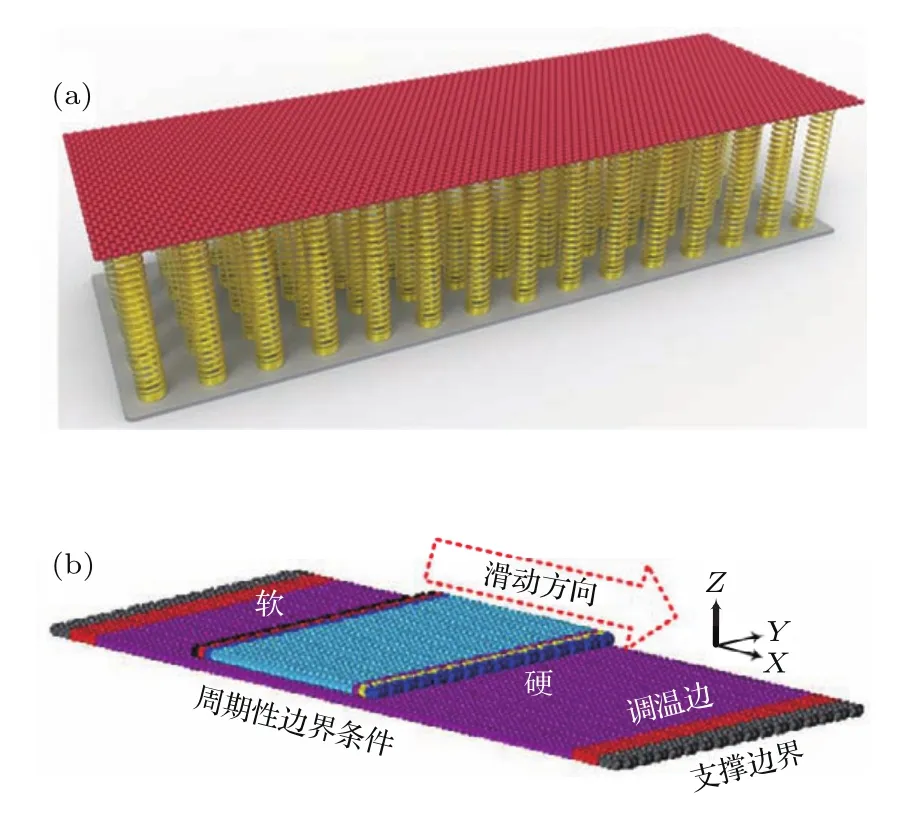
图1 (a)“弹簧床”刚度梯度变化支撑的石墨烯模型;(b)石墨烯薄片-基底摩擦滑动模型Fig.1.(a)The graphene anchored on a bed of stiffness gradient springs;(b)illustration of the model system where the flake(mainly cyan color)slides on a monolayer suspended graphene(purple color).
3 刚度梯度对摩擦力和法向载荷的影响
根据以上模型系统,给薄片每个原子施加0.5 nN的法向面载荷,分别计算不同基底质心刚度(midpoint stiffness,m)和刚度梯度(stiffness gradient,g,且g=∂k/∂x,其中k为法向支撑刚度,x为基底石墨烯在X方向的总长)(单位m,nN/nm;g,nN/nm2)下瞬时摩擦力Fric和平均摩擦力Ff与滑移时间T的关系.由于基底支撑刚度以线性梯度增加,且外驱动滑块速度恒定,单位时间内薄片滑移距离相等.因此,平均摩擦力可取某一时段内瞬时摩擦力的平均值,本文取0.25 ns.这是因为结合石墨烯晶格常数,在0.25 ns内恰好完成了3个瞬时摩擦力黏-滑周期,1.25 ns的滑移时长恰好完成了5个平均摩擦力的统计时间.由图2(a)—(c)可知,随着薄片从较软区域向较硬区域滑动,平均摩擦力逐渐减小,当滑移时间超过1 ns时,平均摩擦力基本保持恒定.并且当m=12时,g越大,最大瞬时摩擦力(圆圈处)和平均摩擦力的下降幅度均越大.例如,当g=1.34时,Ff从6.50 nN下降到3.65 nN;g=1.84时,Ff从22.26 nN下降到4.78 nN,负号表示摩擦力与滑动方向相反.导致以上变化的原因是本文建立的梯度刚度支撑系统可以模拟基底支撑约束下不同层数的石墨烯,随着支撑刚度增大,相当于石墨烯层数增加[32],导致摩擦能耗减小[33],当刚度超过一定临界值时,弹簧支撑的石墨烯系统相当于石墨,平均摩擦力不再减小[34].以上两种条件下探针滑移至1 ns时摩擦系数均为0.005,与已有的实验[35]和仿真[33]结果有相同的数量级,说明了此模型的正确性.本文所有的误差棒均是在5个不同随机速度种子数下计算结果平均值的标准差.
为了模拟力控制接触模式的AFM扫描过程,用反馈信息调整针尖吸附薄片在Z方向的位置,确保法向载荷恒定的同时尽量减小针尖吸附薄片的振荡,因此本文所施加的法向载荷是确保薄片恒高的弹性面载荷.然而随着刚度的增大,有效法向总载荷Fn从896 nN分别增大到898 nN(g=1.34)和901 nN(g=1.84),如图2(d)所示.这是由于支撑刚度较大时,基底法向变形小[33,36],薄片和基底之间的距离变小,层间范德瓦耳斯力增大.根据传统Prandtl-Tomlinson模型[37]可知,法向载荷增大时增加界面势垒高度,导致摩擦力增大.然而图2(c)的结果表明,法向载荷增加引起的摩擦力增加值不足以抵消刚度增大导致的摩擦力减小值,这更说明了刚度梯度对摩擦力有显著影响.

图2 瞬时摩擦力(a),(b),平均摩擦力(c)和有效法向总载荷(d)与刚度梯度的变化关系Fig.2.The dependence of instantaneous friction force(a),(b),average friction force(c)and total normal force(d)on linear stiffness gradient.
4 薄片和基底各接触区对摩擦力的贡献
为了明晰刚度梯度和质心刚度对摩擦力的影响,本文将探针吸附薄片划分成7个区域(沿刚度增大方向依次为T1—T7),除T4(1408个原子)在X方向包含22列原子外,其余各区(64个原子)均包含1列原子,如图3所示.通过分析各区在m=12,g=1.34下所受的摩擦力(X方向的范德瓦耳斯力)可知,在整个滑移过程中T1和T2所受的摩擦力为正,其余各区摩擦力均为负,并且所有划分区的摩擦力绝对值均随刚度的增大而减小.将T4所受的摩擦力平均到每列原子后发现,各区每列原子所受的摩擦力Tif(i取1—7,总摩擦力排序为T1f>T2f>0>T5f>T3f>T4f>T6f>T7f,如图4所示.也就是说,T1f和T2f不但没有贡献摩擦力,反而驱动薄片向前滑动,T7f贡献的摩擦力最大.如果将每列原子的摩擦力占总摩擦力的比值定义为摩擦贡献比,那么在整个滑移过程中,T1f对总摩擦力的贡献比为-36%—-39%,T2f的贡献比为-7%—-10%,负号表示T1f,T2f与摩擦力的方向相反,即为驱动力.随着支撑刚度的增大,T7f对总摩擦力的贡献比也越高,从33%上升到47%,约为T3f—T6f贡献比的4—15倍.
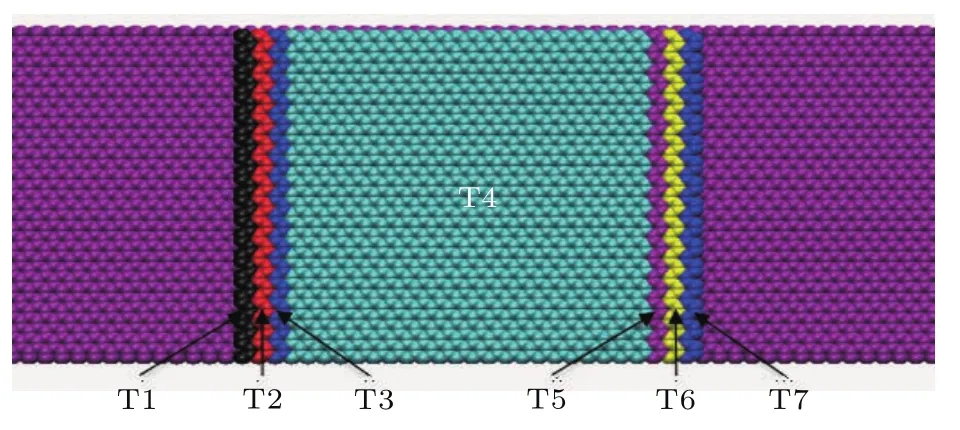
图3 薄片各区划分示意图Fig.3.The schematic of different regions of graphene flake.

图4 薄片各划分区所受的摩擦力Fig.4. The friction force of different regions of graphene flake with a stiffness gradient 1.34 nN/nm2 and a midpoint spring stiffness of 12 nN/nm.
摩擦力是两相对运动的摩擦副接触面间各种力的合力[5,38].为了理清基底对薄片各接触区摩擦力的影响,本文分别对m=17,g=2.68下薄片各区域所对应的基底接触区S1—S7(Ti对应Si)以及接触边界过渡区外延处S0和S8的原子振动幅值(标准差)AF和法向变形量进行统计,如图5所示.结果表明,较大的基底支撑刚度会抑制原子的热运动,同时S0和S8处的原子热振动幅值明显高于相邻接触区,说明原子的热振动不仅受基底支撑刚度的约束,薄片和基底的接触挤压也会抑制原子的振荡.值得注意的是,虽然各接触区原子的振幅各不相同,但是正如图2(d)所示,不同支撑刚度会使各接触区所受的法向载荷不同.因此,只由振幅的高低来判断温度大小的条件已失效[39].在探针未滑动时,由于弛豫热平衡效应,虽然各原子的振幅不同,但系统内温度仍处处等于300 K.根据能量均分定理[39],温度处处相同的原子其振动速度也相同.因此,即使原子的动能相同,其振幅仍可能不同.此外,在不同的法向载荷作用下石墨烯的法向热振动态密度会随载荷的增大向高频偏移[40-42].因此,虽然刚度梯度不能改变弛豫后各区域的温度,但是可以影响不同区域原子的振动模式.由于本文所施加的法向载荷是保证探针薄片恒高的弹性面载荷,因此在不同刚度支撑的区域探针和基底之间的距离不同,在接触边界过渡区两侧(图中椭圆处)形成了非对称变形.图5(b)为滑移过程中法向非对称变形量的演化过程,由图可知,S0和S8处始终形成非对称变形差.因此,各接触区的摩擦力是薄片和基底之间的褶皱势和接触区产生的法向变形差两部分的共同作用.前者是公度接触下阻碍滑移的界面势垒和刚度梯度方向上不同刚度支撑原子热振动引起的势梯度;后者是接触边界过渡区两侧原子的非对称变形和自由度约束突变引起的非平衡边界势垒相耦合的结果.两者在刚度梯度方向上形成了力差,共同合成摩擦力.

图5 (a)基底各接触区原子的热振动幅值;(b)基底各接触区原子的法向变形量Fig.5.The standard deviations of the vibration magnitudes(a)and the normal deformation(b)of substrate atoms outside and within the contact area against the spring stiffness.
4.1 界面势垒和产生驱动力的诸因素对摩擦力的影响
界面势垒高度随着刚度的增大而减小,导致阻碍力逐渐下降;同时,由前文所述,产生驱动作用的因素有刚度梯度方向上接触区内原子热振动引起的势梯度、接触边界过渡区两侧原子的自由度约束突变和法向非对称变形差等,以下分别对各驱动影响因素进行分析.
1)接触区内原子热振动引起的势梯度.基底支撑刚度较小处的原子热振动幅值较大,刚度较大处的原子热振动幅值较小,这种振动幅值的不同产生了刚度梯度方向上范德瓦耳斯势能差而形成驱动力[24].类似于温度梯度方向上原子振动幅值差形成的热驱动力[39,43]、施加电压梯度产生的非均匀性热流形成的范德瓦耳斯势能差[44]以及器件连接边界过渡处热振动幅值差形成的驱动作用[45],驱动力的产生过程可由石墨烯层间的势能[20]来阐释,其中kvdW为范德瓦耳斯力常数,µi为第i个原子偏离平衡位置(0.34 nm)的位移.而当支撑刚度增大时,势梯度引起的驱动力减小,对阻碍力的抵消作用减弱.
2)接触边界过渡区两侧原子的自由度约束突变引起的势梯度.当基底支撑刚度相同时,支撑刚度对基底原子的振动约束相同,由于每个探针薄片原子受到均匀的法向面载荷,基底的法向变形对称,接触区边界两侧原子的约束也对称,在某一温度下基底原子的振幅呈对称的“凹”字型.而当支撑刚度梯度变化时,基底原子的振幅图呈非对称“凹”字型,如图5(a)所示.可以看出,薄片改变了基底的范德瓦耳斯势能面,在薄片和基底的有效接触区,基底的势能面存在一势阱,并且在薄片和基底接触区的边界处有非常明显的势能梯度.薄片T1或T7中某一点的范德瓦耳斯势能场是由基底中与该点相近的许多原子共同引起的,而这些原子中一部分在有效接触区,这部分原子受到薄片的挤压限制,热振动幅值较小,而另外一部分原子在接触边界过渡区外延处(如S0和S8),这些原子不受薄片的约束而热振动较剧烈,这种边界处原子振动幅值的不同会在刚度梯度方向上形成势梯度.其实,即使在刚度梯度为零时,接触边界两侧低约束原子的热振动幅值也明显高于受挤压区域原子的值.当基底质心刚度较小、刚度梯度较大时,接触区边界两侧原子约束差异明显,导致基底的非对称“凹”字型势能面势阱较深,从而接触界面势垒高度较大,摩擦力较大.而当基底质心刚度较大、支撑刚度梯度较小时,接触区边界两侧原子的约束均较强,热振动幅值之差不明显,导致接触界面势垒高度较小,摩擦力也较小.
3)接触边界过渡区两侧原子的法向非对称变形差引起的势梯度.T1在较软的边界过渡区,而T7在较硬的区域,由图5(b)的演化过程可知,两者在法向方向上的变形量始终不同,这种非对称变形差会产生驱动力,但是随着支撑刚度的增大,变形差逐渐减小,由变形差引起的驱动力也逐渐消失.
综上,在刚度梯度增大的方向上,存在产生阻碍力的摩擦副界面间势垒高度的减小和引起驱动作用的诸因素(原子热振动差、自由度约束突变和非对称变形差)使驱动力减小的“竞争”耦合作用.
4.2 刚度梯度对各划分区摩擦力影响的内在机理
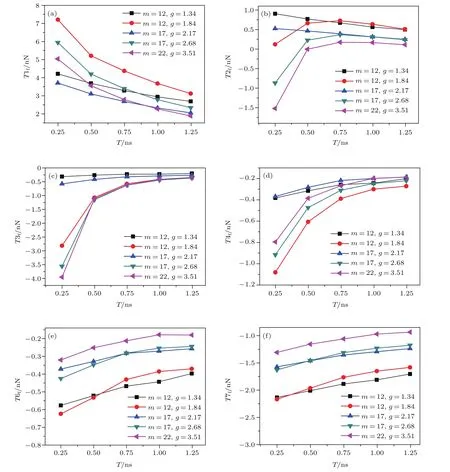
图6 不同基底质心刚度和刚度梯度下薄片各划分区所受的摩擦力Fig.6.The friction force of each region of graphene flake with different stiffness gradient and midpoint spring stiffness.
根据以上理论分析,为了探究和理清刚度梯度对T1—T7各划分区摩擦力影响的内在机理,分别对m=12,17,22以及g=1.34,1.84,2.17,2.68,3.51下各区X方向的范德瓦耳斯力进行计算,如图6(a)—(f)所示(省略T5f).模拟结果及具体解析如下:1)在本文m和g的所有取值下,T1f的方向始终与滑动方向一致,因为T1在接触边界过渡区非对称变形区的“下降”阶段,同时过渡区原子的约束条件突变以及支撑刚度梯度产生的势梯度也会形成驱动力.虽然在滑动过程中界面势垒会产生阻碍运动的摩擦力,但是较大的驱动力足以克服这种阻碍作用而使得T1f在整个过程中表现为驱动力.基底质心刚度越小、刚度梯度越大时,T1f越大,且在滑移过程中下降也越明显.因此,较大的驱动力是由较小的质心刚度和较大的刚度梯度共同作用产生的.2)当m=12,g=1.34时,T2f恒为正且随刚度增加单调下降,此时接触变形和刚度梯度产生的驱动力完全能克服界面势垒的阻碍.随着刚度的增大,接触区变形量和界面势垒高度均下降,导致T2f单调减小.但在m=12,g=1.84时,T2f随刚度的增大先急剧增大随后再缓慢减小.因为g较大时,T2所在的初始位置较软,较高的界面势垒抵消了部分由非对称变形和刚度梯度引起的驱动力,随着薄片向较硬区域滑动,界面势垒高度快速下降,接触区变形和刚度梯度引起的驱动力占主导,导致T2f急剧上升.此后,随着刚度的增大,接触区变形量减小,使得T2f变小.而当m较大(17,22)且g也较大(2.68,3.51)时,随着薄片的滑动,T2f最初为摩擦力,随后变为驱动力再单调下降.这是由于基底质心刚度较大,在滑动初始位置,界面势垒引起的摩擦力大于接触区非对称变形“下降”段和刚度梯度引起的驱动力,使得T2f最初为阻碍力.但随着刚度的增大,界面褶皱势减小,在0.5 ns时,界面势垒已不足以抵消驱动力,使T2受力变正.此后,非对称变形区“下降”段的变形量和势垒高度均随刚度的增大而减小,致使T2f逐渐变小.3)T3—T6各区两侧的非对称变形趋势减缓,摩擦力主要是以克服界面褶皱势而引起的剪切作用力,且随着刚度的增大,界面势垒高度减小,摩擦力的绝对值减小.由于T7为接触边界过渡区,接触区边界两侧始终形成非对称变形的“上升”阶段,变形量较T3—T6明显,同时过渡区原子的约束条件突变也会产生摩擦力,而且T7一直处在较硬区域,阻碍滑移的界面势垒高度随刚度增加时减小的幅度也较小,因此,T7f明显较T3f—T6f大,且随刚度的增大其值减小的趋势也比较缓和.
在宏观尺度,由于非常小的边界接触面比,边界效应常常被忽略,而在纳米尺度,较大的边界接触面比导致边界力对摩擦有重要的贡献,这也是连续介质理论不能应用在原子尺度摩擦学的重要原因之一.
反映层间原子相互嵌套强弱的层间范德瓦耳斯势能对外驱动克服界面势垒做功起决定作用[28,38,46-49].本文计算了m=12,g=1.84下探针薄片在摩擦滑动过程中和基底石墨烯层间的范德瓦耳斯势能,如图7所示.结果表明,随着薄片质心正下方支撑刚度的增大,每3个黏-滑周期内的平均范德瓦耳斯势能Pave随滑移位移D呈指数上升,如图7(a)所示.这是由于刚度梯度支撑下刚度较大区域探针和基底原子的距离较小,如图5(b)所示.而原子间距对原子间的相互作用势起决定作用[10,14].由图5(a)所示,不同接触区原子的热振幅也不相等,因此热振幅贡献的势能差驱动探针向前滑动,也就是形成势梯度,导致图7(b)显示的瞬时范德瓦耳斯势能Pinst的差(即势垒高度,相邻波峰波谷(蓝色圆圈)之差)随滑移位移D逐渐减小.说明探针在滑移过程中为克服基底的阻碍所做的功逐渐减小.Pinst的差和图2(c)中摩擦力随刚度的变化趋势基本一致,也与相关理论[24,50]和实验[7,51]结果相符.刚度越大,对原子振动的抑制越明显,层间范德瓦耳斯势垒高度越低,摩擦力越小.由于薄片各列原子处在刚度梯度支撑的石墨烯基底上,因此每列原子所受的范德瓦耳斯势能各不相同.本文计算的是薄片和基底之间总的范德瓦耳斯势能,虽然不能反映薄片各列原子的势能情况,但势垒高度随支撑刚度增大而减小的趋势足以说明,支撑刚度不同时,层间范德瓦耳斯势能不同,基底刚度梯度支撑能够产生势梯度.因此,图7(b)中的势垒是阻碍滑移的界面势垒和刚度梯度方向上不同刚度支撑原子热振动差引起的势梯度共同作用的结果.如果当基底刚度恒定时,摩擦力和界面势垒高度成正比[46],而图7(b)中势垒高度随刚度增大的变化较平缓,图2(c)中摩擦力随刚度增大的变化却较明显,二者变化趋势不完全相同.导致这种差异的原因是,除阻碍探针滑移的界面势垒和不同刚度支撑原子热振动引起的势梯度外,在支撑刚度较小区域,影响驱动力的另外两个因素(接触边界过渡区两侧原子的非对称变形差和边界过渡区两侧原子的自由度约束差)均较大,产生的驱动力也较大,导致摩擦力下降较快.而当薄片滑到刚度较大的区域时,产生的驱动力较小,导致摩擦力下降趋势变缓.
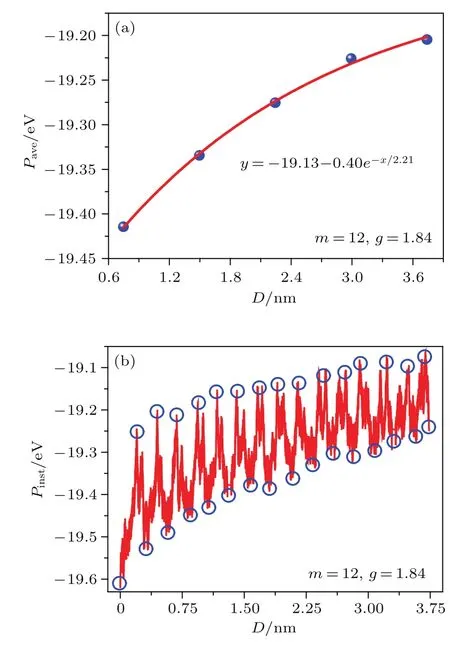
图7 (a)层间平均范德瓦耳斯势能在滑移方向的变化趋势;(b)层间瞬时范德瓦耳斯势能在滑移方向的变化趋势Fig.7.(a)The change trend of average van der Waals potential energy between graphene layers in the direction of sliding;(b)the change trend of instantaneous van der Waals potential energy between graphene layers in the direction of sliding.
5 结 论
基于分子动力学模型,本文研究了公度接触下不同基底质心刚度和支撑刚度梯度变化对石墨烯层间摩擦力的影响.为了探索和理清摩擦能耗的内在机制,将薄片和基底分成边界过渡区和有效接触区,分别讨论各区域对摩擦能耗的贡献.结果表明,各接触区的摩擦力是薄片和基底之间的褶皱势和接触区产生的法向变形差两部分的共同作用.褶皱势是公度接触下阻碍滑移的界面势垒和刚度梯度方向上不同刚度支撑原子热振动引起的势梯度;法向变形差是接触边界过渡区两侧原子的非对称变形和自由度约束突变引起的非平衡边界势垒相耦合的结果.两者在刚度梯度方向上形成了力差,共同合成摩擦力.最后,通过对层间范德瓦耳斯势垒和摩擦力随刚度增大的变化趋势的对比,进一步揭示了刚度梯度对公度接触下石墨烯层间摩擦能耗影响的内在机制.本文皆在探索纳米尺度的摩擦能耗机理,对研究刚度梯度支撑下纳米器件的相对运动规律有重要的指导意义.
