基于Buck变换器控制的压电能量收集电路研究*

魏 胜



基于Buck变换器控制的压电能量收集电路研究*

魏 胜

（深圳职业技术学院 机电工程学院，广东 深圳 518055）

传统的压电能量收集电路在外接优化电阻时效率最高，但实际中外接负载具有多样性，很难实现优化电阻．笔者设计了一种基于Buck变换器控制的压电能量收集电路，可在不依赖外部负载的条件下，保证稳定的直流电输出，提高能量收集效率．对电路工作原理进行理论分析，建立了该电路的输出功率数学模型，设计和制作了储能电路模块，并通过实验验证了电路的工作性能．

Buck 变换器；压电；能量收集；电路

压电振动能量收集技术由于能量密度高、设计简单和集成程度高等原到了广泛的关注和研究，但其产生的功率低且具有交流特性，不适合直接给微电子设备供电，需要经过AC-DC转换及滤波后才能应用于实际电路．另外，压电振动的输出功率在外接优化电阻时的达到最大，且优化电阻与压电耦合系数以及谐振频率有关，而实际中的储能元件如电池或超级电容不具备电阻特性，很难实现优化阻值从而降低收集效率[1]．在使用整流桥和电容的标准储能电路时，随着充电时间的延长，储能电容上的电压rect也会相应地增大，但压电晶片在振动时只能产生正弦交流电p=maxsin，其幅值电压max不变，除了第一个充电周期以外，后续的每个充电周期内都有一个临界点使得rect>p，整流桥发生反偏，压电振动产生的电能无法给电容充电，随着充电过程的持续，每个充电周期储存的能量将越来越少，导致收集效率降低[2]．

为解决这一问题，Ottman等人在收集电路中增加了DC-DC变换器，强调在给定的激振频率下优化占空比系数来提高能量收集效率，但需要一个附加的控制电路来优化能量输出，而且电压要大于10V才可以工作，不适合自供电设备[3]．而采用Step-down变换器且工作在非连续模式下（DCM）可以克服上述缺点，但这种电路需要大于25V的开路电压才可以正常工作[4]．Lefeuvre等人采用Buck-boost变换器工作在DCM模式下，通过设置占空比和电感大小，可以实现优化电阻值从而提高能量收集效率[1]．上述研究提出的数学模型都是基于弱机电耦合特性，即压电耦合系数非常小的前提下，在中等或强耦合条件下并不能起到提高收集效率的作用[5]．更多非线性收集电路的原理分析及总结可参见文献[6]．

本文设计一种基于Buck变换器控制的压电能量收集电路，建立了该电路的输出功率数学模型，设计和制作了储能电路模块，并通过实验验证了电路的工作性能．

1 能量收集模型

根据振动原理和压电方程建立压电振动能量收集系统的动力学模型如下[7]：

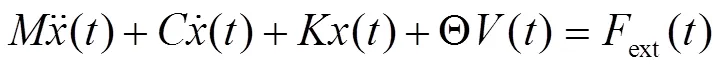
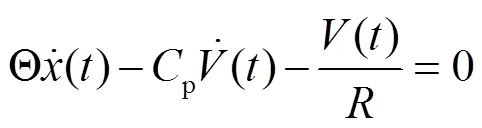
式中，和分别表示系统的质量、弹性系数和阻尼；和p分别表示压电应力系数和压电电容；()和()分别表示压电梁输出电压和位移；ext为外部作用力；表示外接电阻的大小．

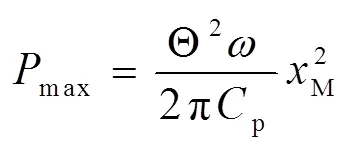
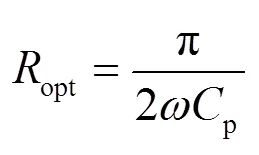
式中M为压电梁振动的位移幅值；为振动频率．

图1所示为接Buck DC-DC变换器的压电能量储能电路原理图．其中，整流桥的二极管假设为理想状态，Buck变换器用于控制输出电压V为恒定值，相当于压电材料外接非线性负载[9]．

输出电压及位移幅值的波形如图2所示．当压电电压低于c时，整流桥截止，输出电流out为0．当压电电压达到c时，输出电压不变．随着振动幅值M的减小，压电电压低于c，整流桥再次截止，如此反复．在0至0时间段内，（2）式可以表示为：

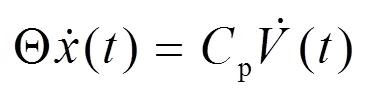
可见，此时输出电压与振动位移成正比．而在t0至T/2时间段内，输出电压保持恒定值Vc．

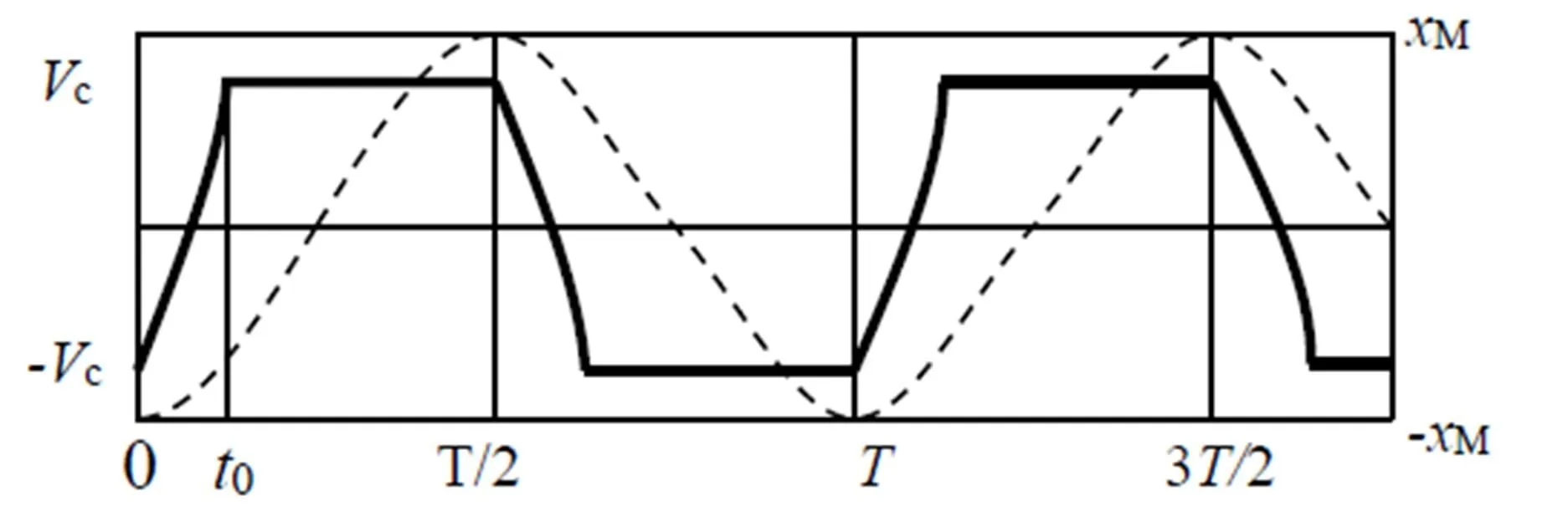
图2 输出电压及位移幅值波形图

假设外部作用的谐振力与压电梁的振动相位不同，根据图2所示的波形图令压电梁振动位移表达式为()Mcos(-π)，而外部振动表达式为()Mcos(+-π)在0至2半个周期内，输出电流为：

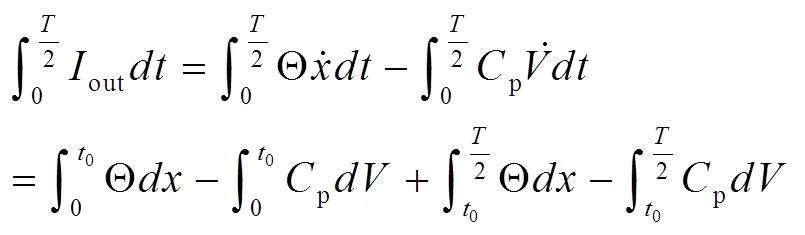
在0至0时间段内，out=0，所以：

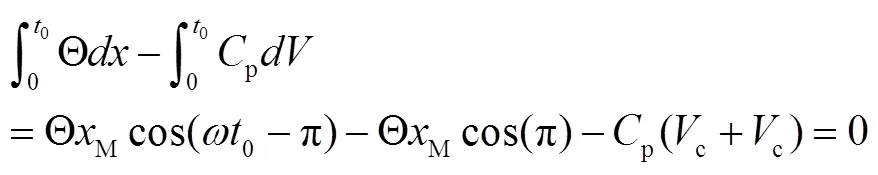
而在0至2时间段内c保持不变，所以：

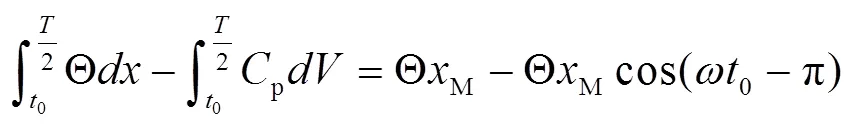
上述三式联合求解可得：

在0至2半个周期内，输出功率为：

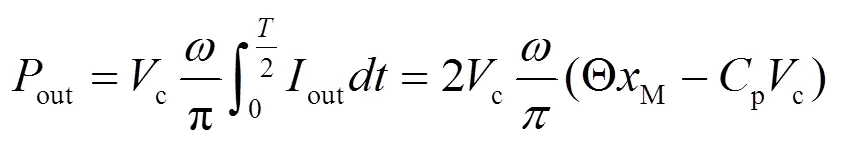
由上式可知，当c为优化值时，输出功率out最大．公式（10）对c微分后可得：

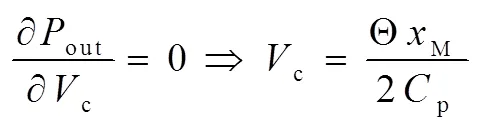
最大输出功率为：

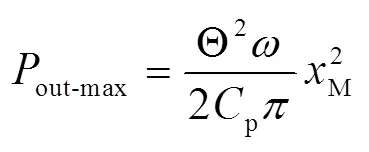
比较公式（3）和（12）可知，2种电路获得的最大功率相同．

2 电路设计

本文采用LTC3588和LTC3009芯片来设计和制作压电振动储能电路．LTC3588是由Linear公司新推出的用于采集和优化低压能源的芯片，作为一个高效降压型DC/DC变换器，其输入电压范围2.7~20V，连续输出电流高达100 mA．LTC3009也是由Linear公司推出的低压差线性稳压器，具有多种固定的输出电压，而且可以通过引脚的外接电阻来调节输出电压，其输出处于稳定状态时静态电流仅为3μA．

图3所示为利用LTC3588和LTC3009芯片设计的储能电路原理图．LTC3588有一个内部的全波整流桥，可将压电元素由输入的交流电进行整流；整流后的电能暂时存放在与引脚VIN相连的电容2上；当引脚VIN上的电压达到UVLO所控制的上限临界值，Buck变换器导通，电荷从输入电容2传输至输出电容4上．当输入电容的电压低于UVLO所设置的下降临界值时，Buck变换器断开，如此反复．在这种工作模式下负载电流由Buck模块的输出电容提供．通过连接引脚D0和D1可以实现四种可选的输出电压，图4的连接方法保证输出电压为3.6V．输出电压VOUT引脚连接LTC3009线性稳压器的输入端，可将输出电压调节至稳定的3.3V．

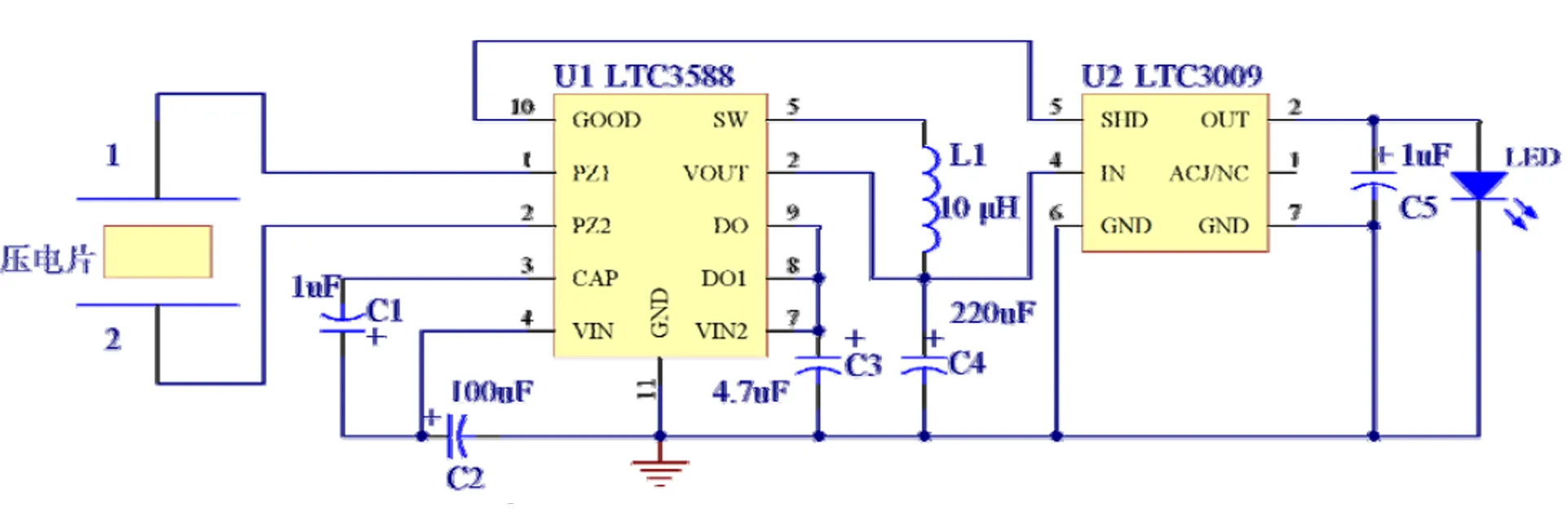
图3 Buck 变换器储能电路设计原理图

3 实验结果

图4所示的振动实验平台．压电梁安装在Labwork ET-126型号的电磁激振器上，并通过Tektronix DPO4054示波器来测试其输出电压；同时激振器上还附加安装了加速度传感器用于检测实时的振动加速度．另外，压电悬臂梁选用型号为Q220-A4-203YB的压电晶片，该晶片采用PSI－5A4E型压电材料，由PIEZO Systems, Inc.公司生产．实验中在压电晶片的自由端粘贴了0.3g的质量块用于降低谐振频率，实际测试压电梁的谐振频率约为171Hz．

图5所示为储能电路模块的实验原型装置，依据图3所示的原理图来设计和组装．在实验过程中，首先将压电梁直接与外部电阻相连，用于测试压电梁在特定振动条下所能产生的最大功率．

图6表示压电梁在3g（g=9.8 m/s2）的振动加速度下和谐振频率条件下，其输出电压和功率随外接负载值变化的曲线图．从图6可以看出，压电梁的输出电压与外接负载成正比，而输出功率则是先增大后减小，最大输出功率max=0.424 mW发生在阻值为65 kΩ时，此时输出电压为5.25V．由此可见压电梁在谐振时，其输出功率在外接优化电阻时达到最大．由于外接Buck变换器电路所产生的最大功率与直接电阻相连的条件下相同，所以上述实验结果可以作为后续储能电路的实验提供参考．

图4 实验布局图

图5 储能电路模块实物图

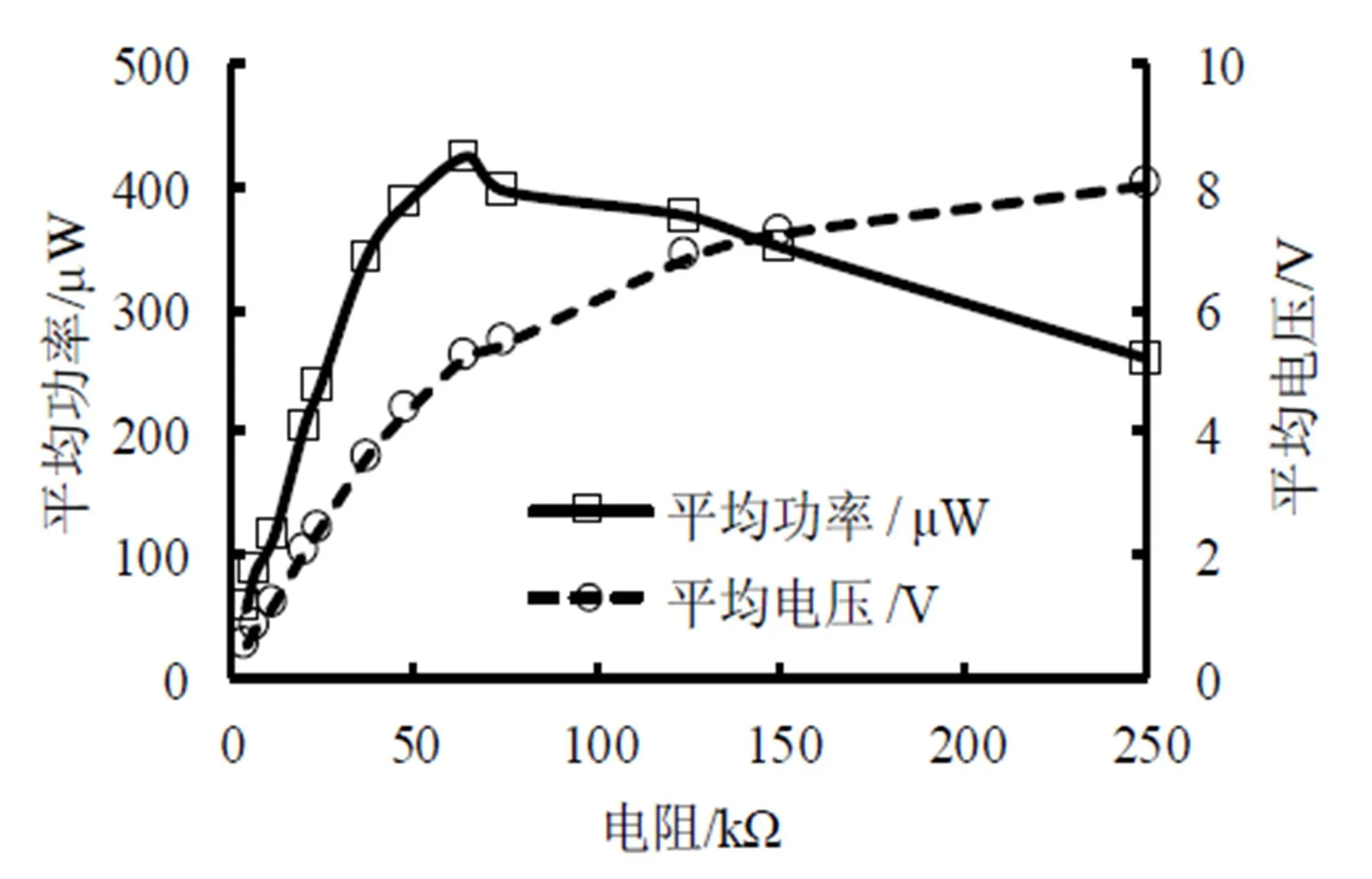
图6 压电梁输出电压和功率曲线图

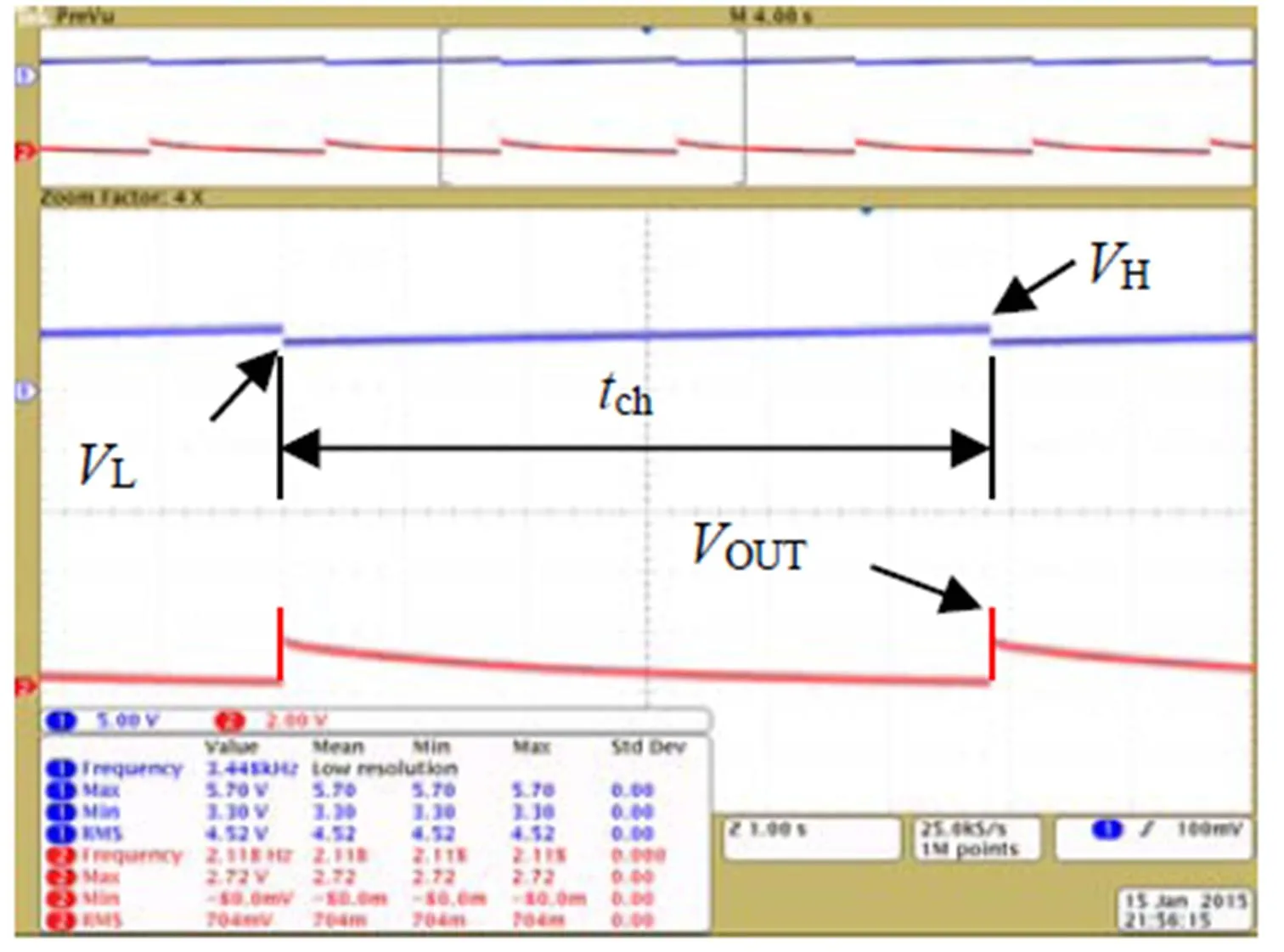
图7 储能电路充电图

将压电梁的输出端连接储能电路模块并在相同的外部振动条件下进行实验测试．图7所示为在多个实验周期的示波器截图，其中蓝色的折线表示储能电容4（220μF）的电压变化，而红色的垂直线则表示电压调节器（LTC3009）输出电压的变化．由图可知，电容在经历ch=6s的充电时间后开始放，输出电压OUT为2.72V．而每次充电的过程中电容电压从L=3.3 V上升到H=5.3V，实验结果与理论设定值比较接近．

根据实验数据可知，在一个充电周期内储能电容的电压从3.3V上升到5.3V，其储存的电能可以表示为：

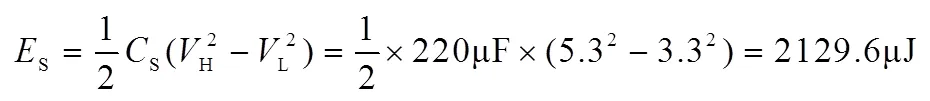
而在充电周期内（ch=6s），压电梁可以产生的最大电能约为：

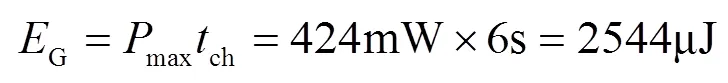
对比式（13）和（14）可知Buck储能电路的效率约为83.7%．为了测试电路的稳定性，将电路中的储能电容4替换为1000 μF，然后在相同的外部激励条件下再次进行测试，并将实验数据前面的进行对比，详情参见表1．由表可知，当储能电容较小时，到达导通电压H所需的充电时间较短（6s），相比大电容来说储存的电能较少，相应的负载工作灯的亮灯时间（8ms）也小于大电容确保的亮灯时间（32ms）；但2种储能电容在工作时电路的导通和截止电压相同，输出电压也同为2.72V，而且储能效率十分接近，说明该储能电路的控制性能稳定．

表1 不同储能电容的实验数据对比

[1] Lefeuvre E, Audigier D, Richard C, et al. Buck-Boost Converter for Sensorless Power Optimization of Piezoelectric Energy Harvester[J]., 2007，22（5）：2018-2025．

[2] Wu W J, Wickenheiser A M, Reissman T, et al. Modeling and experimental verification of synchroniz- ed discharging techniques for boosting power harvesting from piezoelectric transducers[J]., 2009，18（5）：4005-4021．

[3] Ottman G K , Bhatt A C, Hofmann H F ,et al. Adaptive piezoelectric energy harvesting circuit for wireless remote power supply[J]., 2002，17（5）：669–676．

[4] Ottman G K, Hofmann H F, Lesieutre G A. Lesieutre. Optimized Piezoelectric Energy Harvesting Circuit Using Step-Down Converter in Discontinuous Conduction Mode[J]., 2003，18（2）：696-703．

[5] Shu Y C, Lien I C. Efficiency of Energy Conversion for a Piezoelectric Power Harvesting System[J]., 2006，16：2429-2438．

[6] Guyomar D, Mickaël Lallart. Recent Progress in Piezoelectric Conversion and Energy Harvesting Using Nonlinear Electronic Interfaces and Issues in Small Scale Implementation[J]., 2011（2）：274-294．

[7] Liao Y, Sodano H A. Structural Effects and Energy Conversion Efficiency of Power Harvesting[J]., 2009，20（5）：505-514．

[8] Lefeuvre E, Badel A, Richard C, etal. A Comparison between Several Vibration-powered Generators for Standalone Systems[J]., 2006，126（2）：405-416．

[9] D'Hulst R, Sterken T, Fiorini P, et al. Energy scavengers: modeling and behavior with different load circuits[C] /33rd Annual conference of the IEEE Industrial Electronics Society (IECON 2007). IEEE, 2007：2169-2174．

Research of Piezoelectric Energy Storage Circuit Based on Buck DC-DC Converter Control

WEI Sheng

（）

Traditional piezoelectric energy harvesting circuit achieves maximum efficiency with optimized resistances. However, the external loads are variable and hard to achieve the optimized resistances. A storage circuit with buck DC-DC converter is designed which provides steady DC current whatever the external loads are. The principle of the circuit is analyzed and the numerical modeling of the output power is established. The storage circuit module is fabricated and the performance is verified by experiments.

Buck converter; piezoelectric; energy harvesting; circuit

10.13899/j.cnki.szptxb.2019.01.002

2018-07-03

深圳科创委基金资助项目（GRCK2017041917042682）

魏胜（1976-），男，湖北孝感人，博士，副教授，主要研究方向为压电能量收集．

TM46

A

1672-0318（2019）01-0010-05