城市轨道交通车站节假日售票组织优化模型研究

龙思慧，丁 勇

（北京交通大学 交通运输学院，北京 100044）

1 概述

城市轨道交通售票系统通常由自动售票机、人工客服窗口、人工售票窗口组成平行排队的多服务台系统，乘客到达后可以排在任何一个队列中。其中，人工客服窗口可进行购票、票卡充值、票务故障处理、兑换零钱等综合业务，而人工售票窗口只出售单程票。节假日平峰期可考虑减少自动售票机开放数量，降低设备运营成本。人工售票窗口主要根据客流情况动态设置，客流较小的时段可不设置，但高峰期或突发大客流期间，可开放更多人工售票窗口满足乘客购票需求。城市轨道交通售票排队系统示意图如图1所示。

图1 城市轨道交通售票排队系统示意图Fig.1 Queueing system

节假日期间，城市轨道交通车站购票客流会激增，客流在时间上分布不均衡且波动性较大。与通勤高峰客流不同，节假日大客流中包含相当多不熟悉购票操作的外地游客，增加了售票组织的难度，而且车站全日各时段不同类型售票设备的开放方案与企业提供的运输服务水平及运营成本有着密切关系。因此，通过寻求服务水平与运营成本间的平衡点，合理安排节假日期间不同时段售票设备的开放数量，对于提升城市轨道交通运营组织水平具有重要意义。

国内外专家积极开展城市轨道交通车站节假日售票组织方面的研究。张微[1]系统分析了影响用户使用城市轨道交通自动售票机速率的因素；任建华[2]探讨了铁路车站售票组织应急响应启动的条件与时机；张伯敏[3]应用排队论理论探讨铁路车站售票窗口和自动售票机设置优化问题；丁蕾等[4]基于排队论建立BP神经网络模型并预测站点购票客流及自动售票机的需求量。对于排队问题的研究，Roubos等[5]运用排队论中的M/M/n模型对银行营业网点的服务能力决策进行了研究；蒋阳升等[6]将高峰时段城市轨道交通通道客流描述成排队系统，构建了排队优化模型计算城市轨道交通通道宽度；李维峥等[7]综合考虑企业营业费用及顾客由于等待产生的损失费用2个因素，建立以费用总和最小为目标的优化模型，从而求得合理的收费窗口数；李怡娜等[8]对高速铁路客运站的票务设备开放配置影响因素进行分析，提出票务设备功能开放配置优化模型。由此可见，既有研究成果为解决高峰期售票组织问题提供了理论指导，但还不能完全适应节假日客流及售票系统的特征。为此，分析节假日城市轨道交通购票客流及售票系统特征，以全日各时段各类型售票设备开放数量为研究对象，以一定服务水平作为约束，平衡乘客等待时间费用与运营管理费用，构建售票系统总费用最小的售票组织优化模型，设计相应算法进行模型求解，并通过案例验证模型与算法的可行性与有效性。

2 城市轨道交通车站节假日售票组织优化模型构建

2.1 建模思路

根据城市轨道交通车站实际运营状况，全日每个时段都固定开放1个人工客服窗口，构建节假日车站售票组织优化模型，计算自动售票机与人工售票窗口数量，达到售票系统总费用最小。城市轨道交通车站提高售票服务水平(如增加售票设备数量等)会降低乘客等待时间费用，但同时会增加车站运营管理费用。售票系统总费用与运营管理费用、乘客等待时间费用关系示意图如图2所示。

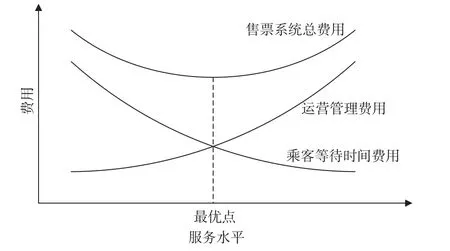
图2 售票系统总费用与运营管理费用、乘客等待时间费用关系示意图Fig.2 Relationship of the operating cost, waiting cost and the total cost

只有服务水平在最优点处，售票系统总费用才能最小。乘客等待时间费用和运营管理费用都是服务水平的函数，其中前者是服务水平的减函数，后者是服务水平的增函数。当售票系统总费用最低时，服务水平与运营成本达到综合最优。因此，应综合考虑乘客等待时间费用和运营管理费用，实现售票系统总费用最低。

2.2 模型构建

假设在进行购票设备选择时，乘客考虑的因素只有窗口前排队等待时间；一定时间内到达售票系统的乘客数服从泊松分布；售票服务时间服从负指数分布。将运营时间以1 h为间隔划分为n个运营时段，考虑该时段不同类型售票设备的服务率与服务强度、售票设备前排队队长、站厅对于售票设备数量的限制、工作人员数量等，通过约束上述条件使得售票服务满足一定的服务水平。

以售票设备的运营管理费用与乘客等待时间费用之和最小为目标函数，以服务强度、售票设备前排队队长及售票设备数量为约束条件，建立节假日车站售票组织优化模型如下。

式中：Z(Ca，Cb)为售票系统总费用，其中Ca为开放自动售票机的数量，Cb为开放人工售票窗口的数量；θa，θb分别为开放单位自动售票机、人工售票窗口的费用；ω表示乘客等待时间费用与运营管理费用的转换关系；Lqk(Ck) =f(Ck)，表示开放Ck个售票设备期望排队队长，Ck为售票设备开放数量的因变量，f(Ck)由售票系统排队方式决定，k=a，b；xi为是否开放人工售票窗口的0-1决策变量，xi= 0表示在开放自动售票机能满足购票客流需求的情况下，不开放人工售票窗口，反之开放人工售票窗口，即当时，xi= 0，当时，xi= 1，其中，λa为平均每小时到达自动售票机的乘客数，μa为该自动售票机平均每小时可以服务的乘客数，ρamax为自动售票机最大服务强度参数；ρb为人工售票窗口服务强度，其中λb为平均每小时到达人工售票窗口的乘客数，μb为人工售票窗口平均每小时可以服务的乘客数；ρbmax为服务强度上限；ρbmin为服务强度下限。

公式 ⑵ 表示人工服务强度约束；公式 ⑶ 表示排队队长约束；公式 ⑷ 表示售票设备数量约束。

2.3 模型求解

在节假日车站售票组织优化模型中，只有系统队长和不同类型售票设备开放数量为变量，并且系统队长为售票设备开放数量的因变量，售票设备数量只能取正整数，设售票设备开放数量集合为U，结合公式 ⑵ 至公式 ⑷，解集合U表示为

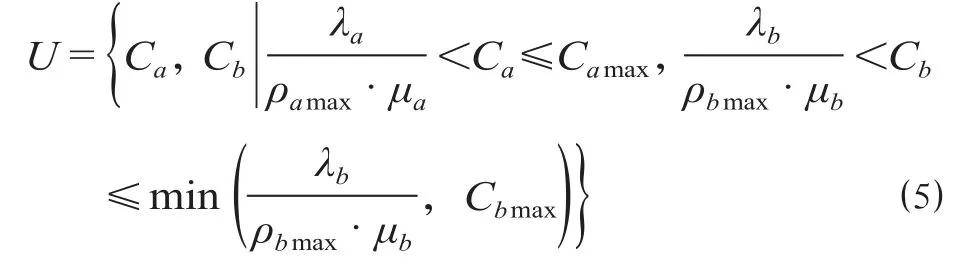
由于目标函数为非连续变量的函数，不能采用经典的微分法求最优解，基于WinQSB计算模型总费用，采用边际分析法得出售票设备开放数量最优解。

采用边际分析法，，应满足经代入参数，得到以下公式

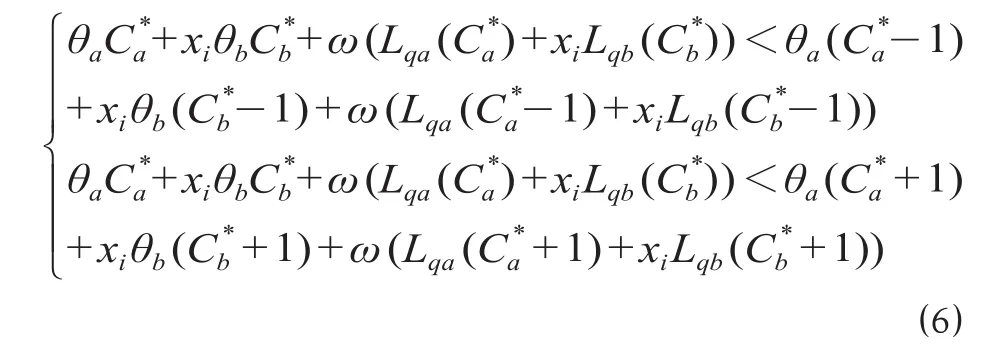
根据边际分析法计算最优解，，通常会出现以下2种情况：①若和均属于解集合U，则最优解和由公式⑹确定；②反之，若存在或不属于解集合U，则最优解和由来确定。

3 案例分析

小寨站是西安城市轨道交通2号线的一个车站，处于小寨商圈核心地带。车站北边售票处8台自动售票机构成平行排队的8个M / M / 1 / ∞ / ∞ / FCFS排队系统，人工客服窗口为1个M / M / 1 / ∞ / ∞ / FCFS排队系统，人工售票窗口为1个M / M / 1 / ∞ / ∞ / FCFS排队系统。小寨站售票系统排队模型如图3所示。

图3 小寨站售票系统排队模型Fig.3 Queueing model of ticketing system on Xiaozhai Station

3.1 模型求解

（1）乘客时间价值。乘客时间价值在此采用收入法进行估算，估算公式为

式中：VOT为乘客单位小时内的时间价值；INT为人均年收入；T为年工作小时量。

根据西安市乘客月可支配收入结构，计算出人均年收入为50 913.6元，乘客年工作小时量为1 992 h，则旅客时间价值VOT= 50 913.6 / 1 992≈25.6元/ h。

（2）运营管理费用。主要包括员工工资、机器折旧费、耗损费用等。通过实地调研，推算出站内自动售票机、人工售票窗口运营成本分别为15.2元/h和43.7元/h。

（3）参数取值。通过对小寨站北边售票处2016年节假日乘客购票情况的调研，根据小寨站运营情况、高峰小时购票乘客人数、客流分布特点及站厅容量限制，确定服务指标为：ρamax= 0.99，ρbmin= 0.70，ρbmax= 0.80，Lqamax= 10，Lqbmax= 30，Camax= 12，Cbmax= 2。其中，为满足高峰小时乘客数，车站需在现状8台自动售票机的基础上增加4台自动售票机以缩短乘客等待时间。根据对人工客服窗口处乘客数量及购票需求进行调查，可得全日各时段需要在人工客服窗口购票乘客数量的平均值为65人。

（4）乘客平均到达率。对运行时段6 ∶ 30—23 ∶ 30进行小寨站购票客流调研，经数据分析得出全日各时段乘客平均到达率(减去接受人工客服窗口服务乘客数65人后的售票系统总的到达率)。乘客平均到达率如表1所示。

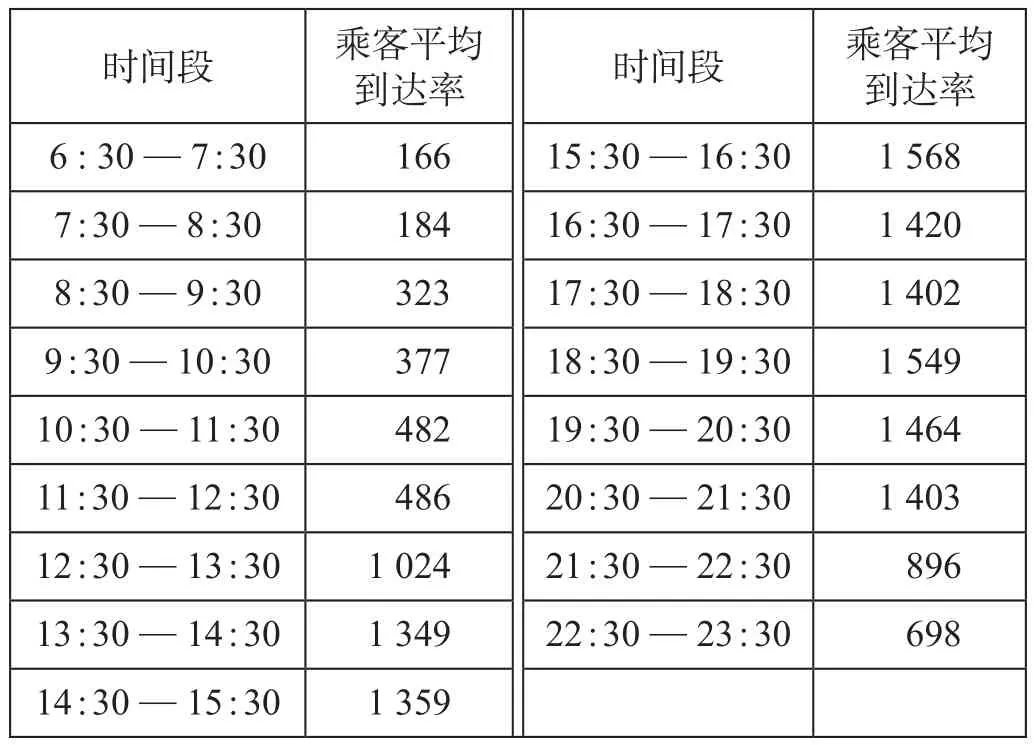
表1 乘客平均到达率 人/ hTab.1 Average arrival rate of passengers

（5）售票设备平均服务率。通过对不同售票设备进行客流调研可得自动售票机、人工售票窗口平均服务时间分别为33.2 s /人、10.6 s /人，即单位时间(1 h)可以服务的乘客数分别为98人、355人，取μa= 98人/ h；μb= 355人/ h。

3.2 优化结果分析

在实地调研数据的基础上，计算得出各时段不同类型售票设备开放数量的优化方案。售票组织优化方案如图4所示。

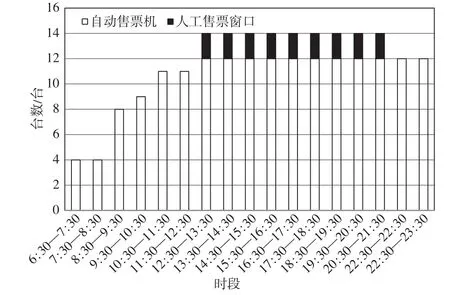
图4 售票组织优化方案Fig.4 Optimized scheme of ticketing organization

从图4可以看出，售票设备开放数量由现状各时段固定开放8台自动售票机变为根据不同时段客流变化特征进行调整，其中每一时段需固定开放1个人工客服窗口。在客流量较少的时段，如6 ∶ 30— 7 ∶ 30，售票系统总费用最小的方案为开放4台自动售票机，相较现状减少开放4台自动售票机，降低了运营管理费用。客流量较大的时段，15 ∶ 30—16 ∶ 30是小寨站客流高峰时段，在该时段开放12台自动售票机及2个人工售票窗口，较现状需增加4台自动售票机，可以有效减少排队队长，提升乘客购票服务质量。通过测算，应用节假日售票组织优化模型计算得到的车站全日不同时段各类型售票设备开放数量的优化方案，售票系统总费用较现状降低约10%，乘客购票平均等待时间降低约30%，在有效缩短乘客等待时间的基础上，提高了售票系统总体效益。

4 结束语

随着城市轨道交通的发展，车站客流不断增长，尤其是节假日期间购票客流会激增，应合理安排节假日期间不同时段售票设备的开放数量。售票组织优化模型能够适应不同时段客流的变化，缓解高峰时段乘客排队购票压力，节省运营管理费用，计算结果对车站节假日期间的售票组织具有一定参考借鉴意义。该研究目前主要考虑了地铁售票设备开放数量对售票排队系统的影响，下一步研究应结合地铁列车运行图、限流设施、售票系统位置等因素进行乘客购票的预测和量化，以更加精确地描述售票排队系统。另外，还需要对乘客的售票设备选择行为进行深入研究，分析售票组织的瓶颈，从而得到更为精细的城市轨道交通售票组织优化模型和售票设备配置方案。