分数Kelvin型粘弹性介质中波的频域分析
2019-01-23高云飞
高云飞
(信阳师范学院建筑与土木工程学院,河南 信阳 464000)
近年来,分数导数理论在机械、生物力学、复合材料及粘弹性材料等研究领域得到了广泛应用。孙海忠[1]对高分子材料的蠕变、松弛等力学行为试验数据进行了比较,对比了传统粘弹性模型和分数阶粘弹性模型对数据拟合的差别,阐述了分数阶粘弹性模型在描述材料粘弹性性能等方面的优越性。刘林超[2]等建立了用分数微分算子表达的分数阶粘弹性模型,并对服从这种分数阶粘弹模型材料的阻尼性能做了分析。杨小军[3]使用广义分数微分算子建立了带有多个参数的幂律核函数的分数阶导数(包括局部分数阶),并推导了广义分数微分算子描述的粘弹性基本元件;通过基本元件的相互组合,对含有广义分数微分算子的粘弹性模型的力学行为进行了分析。由于分数阶模型在表达复杂介质性能上的有效性,Yury[4]等采用渐进公式,对粘弹性介质中的波动方程进行了分析,没有应用分数微积分理论,利用渐进公式克服了数学推导中的一些难题。Sanja[5]等,用分数阶齐纳模型取代经典弹性方程中的胡克应力应变关系,通过对方程向s域的变换,并利用积分公式变换到时域,得出了应力波位移的时域解,分析了分数齐纳模型描述的应力波位移解的特点。本文针对类似的应力波系统,采用分数Kelvin模型代替经典弹性方程的应力应变关系,在频域下求解了分数Kelvin模型描述的应力波位移解的形式,分析了分数阶数以及频率对位移解的影响。
1.分数Kelvin型波动方程的建立
许多岩土材料,譬如土壤和岩石[6]等,其内部结构往往是由复杂介质构成,传统的粘弹性模型不能准确表达其真实的应力应变关系。本研究考察了波在这类复杂介质中的传播。标准的弹性方程可以表示为[7]:
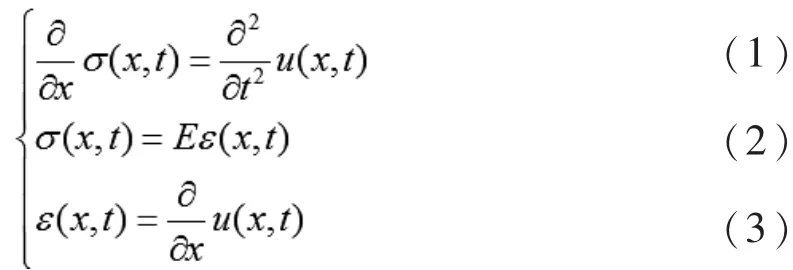
其中,方程(1)为运动平衡方程,式中 σ,u为应力和位移。方程(2)是弹性体的本构方程,也就是经典的胡克定律,其中E为杨氏模量,ε代表应变。方程(3)是在系统满足小变形假设情况下,描述系统的应变位移关系。
我们的讨论是把材料看作复杂粘弹性介质,在传统的弹性理论中,经典的胡克定律不能准确描述粘弹性体的性质。为此,我们把方程(2)用分数Kelvin型应力应变关系取代,用来描述粘弹性复杂介质的性质,即[8]:
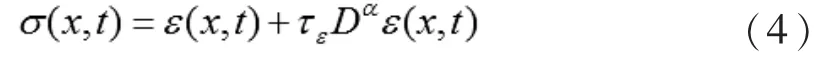
上式即为粘弹体的分数Kelvin型本构关系,其中,Da是 Riemann-Liouville型分数导数[9],表达式为:

其中,0〈a〈1,Г(z)为 Gamma 函数,表达式为:

Da[f(x)]的laplace变换为:

由上可知,分数Kelvin型粘弹性介质中的波的分析模型为:

系统的初始条件设为:

边界条件:

2.波动方程的求解
对方程(4)进行laplace变换:
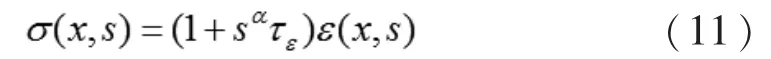
将(3)式带入上式:

将上式(12)带入运动方程(1)可得:

由初始条件(9),方程(13)写为[6]:

对(14)式作 laplace变换:

对式(15),我们令:

则式(15)变为:

上式为二阶常系数线性非齐次微分方程,其解为:
利用初始条件,令su0(x)+v0(x)=1,上式变为:

式中:
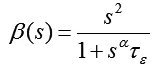
(18)式即为分数 Kelvin型粘弹介质中波的频域解形式。
3.数值算例
由(17)式我们得到频域里的位移解析解形式,这里分析波在譬如土壤和岩石这种复杂介质中的位移解的变化特点。利用MATLAB(9.0;R2016a)数值分析软件,先令频率分别为(10,20,30,50)时,分析波动位移随着横坐标x值的变化,在不同频率下的应变响应,如下图。
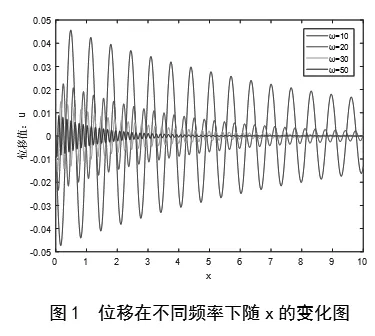

由图1可以看出,角频率对位移变化的影响很明显。在频率较小时,位移值在x较小时会出现较大的震荡;随着x的增大,位移幅值慢慢减小并逐渐趋于零;随着频率的增大,位移的变化幅度出现明显减弱,并会很快趋于稳定。
在低频时(ω=5),当频率为一稳定值时,分别对分数Kelvin模型取不同分数阶数值,位移值随x的不同的变化曲线如图2。在频率较小,α=0.2时,位移呈现出明显的波动,随着x值的逐渐增大,位移的波动慢慢减弱,最后稳定趋于零。而在α值接近于 1时,即 α 值取 0.4、0.6、0.8,相应的位移幅值会出现显著减小,而且趋于稳定的速度变快。
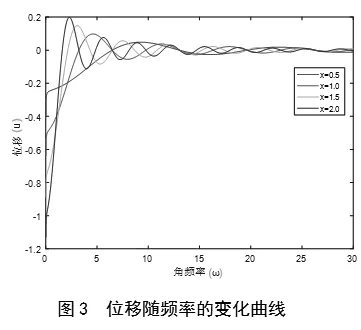
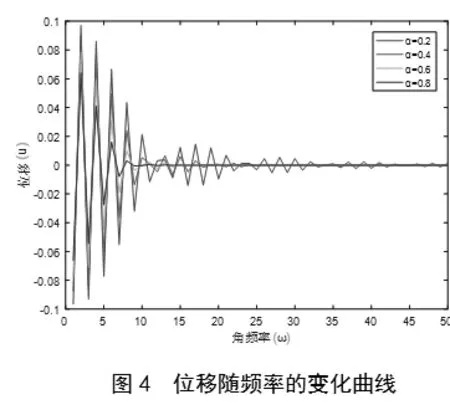
图3为不同位置的x处,位移随频率的变化曲线。图4为不同分数阶数值α对相同位置x处位移的影响曲线。由图3知不同位置x处的位移随频率的变化情况基本一致,而在图4中我们发现,在相同位置下的位移值会随着α值的不同发生明显改变。
4.结论
(1)通过对频域下的波动方程位移解的分析发现,分数导数阶数值α以及频率的高低都会对位移值产生很大的影响。对于传统粘弹性模型来说,分数阶模型能更好地体现应力波在复杂粘弹介质中的扩散。
(2)除了土壤、岩石等岩土材料之外,分数阶模型在复杂介质中的应用还包括超声波在生物组织中的扩散、地震波[6]在土壤岩体中的传播以及在地质、环境工程[10]和水利工程等领域的研究。
