砌体结构高温性能研究进展

张 晋 许清风 章东昊 李维滨 王卓琳

(1.东南大学混凝土及预应力混凝土结构教育部重点实验室,南京 210096;2.上海市建筑科学研究院上海市工程结构安全重点实验室,上海 200032)

0 引 言

目前,砌体结构建筑的数量在城市既有建筑工程中仍占很大比例,且普遍存在人员密集、房屋密度大、消防措施落后等特点。这些因素不仅增加了砌体建筑发生火灾的频率,也使得砌体建筑发生火灾后的危害更加严重。火灾发生后,尽管砌体结构本身不会燃烧,但块体和砂浆在高温下的力学强度会明显降低,极易引起结构破坏,房屋垮塌,甚至造成人员伤亡。

近年来随着生产工艺的进步,除了最初的烧结黏土实心砖,又相继出现页岩多孔砖、煤矸石多孔砖、粉煤灰多孔砖、混凝土多孔砖等,这些都极大地丰富和发展了砌体结构[1],使得砌体结构在将来仍有一席之地。目前国内外对砌体结构的高温性能已经开展了一系列研究,并取得一定的成果,但仍不够全面。因此本文系统地总结了砌体高温性能研究的已有成果,并以图表的方式进行了对比,直观地展示出各方研究的异同,为今后更进一步的研究提供参考和思路。

1 砌体结构的高温性能特点

根据现有的试验和理论研究成果[2-5]以及工程实践经验,砌体结构的高温(火灾)下性能与常温下的性能有很大的差异,具体特点有:

(1) 内部温度场分布。砌体结构的热传导系数很小,结构受火后表面温度迅速升高,而内部的温度增长缓慢,再加上砂浆和块体的导热能力有差异,砌体结构内部形成了不均匀的温度场,且温度场随着火灾时间的延续也会不断发展变化。

(2) 材料性能。高温(火灾)下,块体和砂浆的强度值与弹性模量值将减小,变形增大,材料性能严重劣化。砌体结构相继出现开裂、酥松剥落等外观损伤现象,并随着温度的升高而渐趋严重。

(3) 应力-应变-温度-时间的耦合作用效应。温度值和持续时间都会对材料的力学性能参数造成影响。高温-力学本构关系中,必须考虑应力-应变-温度-时间的耦合作用效应。

(4) 破坏的过程和形态。砌体结构在常温下和高温下的破坏形式均为脆性破坏。但在高温下,裂缝发展更加迅速,破坏过程也更为短促,破坏后的砌体构件变形更大,剥落和碎裂现象更加明显可见。

2 高温下砌体结构的热工性能

目前,国内对这高温下砌体结构的热工性能的研究很少,本节多参考国外研究成果,分别介绍块体、砂浆两种材料的高温热工性能。

2.1 高温下块体的热工性能

块体的热工性能包括比热c、热传导率λ和密度三个方面。影响块体高温下热工性能的因素有很多[5-6]:①当温度达到100 ℃～120 ℃时,块体内部的水分蒸发,将对材料的热工性能有很大影响;②不同材料的块体在高温下所发生的物理化学变化也各有不同;③相比于实心砖,多孔砖内部有许多孔洞的存在,使传热过程变得更为复杂。以上种种影响因素,加大了高温下块体热工性能的分析难度,各学者和机构的研究成果存在一定的出入。

2.1.1比热c

高温下块体的比热取决于很多因素,最重要的是块体中水分的蒸发。研究表明[7],在块体的加热过程中,当温度小于95 ℃时,c基本不变;温度在95 ℃～105 ℃时,由于块体内的水分开始大量蒸发,吸收大量的热量,使c陡增达到峰值;温度升到200 ℃左右时水分基本蒸发完毕,c迅速回落至常温数值附近;温度继续上升,虽然块体材料会因物化反应吸收热量,但吸收热很少,可以看作不影响c。

EN 1996-1-2[8]给出了多种类型的块体随温度变化的比热曲线(图1中给出了两种常见块体的比热曲线),Nguyen[6,9,10]等通过试验研究得到的粘土砖随温度变化的比热曲线,如图1所示(图中相对比热系数,为温度T时cT与20 ℃时比热值c20的比值),反映出块体在100 ℃时,比热数值由于水分蒸发造成的骤然上升。

图1 块体比热随温度变化曲线Fig.1 Evolution of heat capacity of brick versus temperature

2.1.2热传导率λ

影响热传导率的原因有很多,例如:当温度上升时,块体内部物质会发生物理化学变化;对于有孔洞的多孔砖来说,高温下其会产生空腔辐射,从而改变整个多孔砖的λ[11]。Nguyen等[6]通过热学试验发现,300 ℃以下时,黏土砖的λ基本没有变化;随着温度继续上升,由于黏土高温的物化反应使λ发生下降;等温度超过800 ℃,黏土砖膨胀使砖内部的空隙增多,造成空隙内的热辐射传热,又会增强黏土砖的传热能力,λ值上升(λ-T曲线见图2)。Pavlík,Jerman等[12]研究发现,在多孔砖孔洞内填充聚苯乙烯、石棉等材料,可以有效降低多孔砖在高温下的空腔辐射,从而降低λ约50%。Ayala[3]认为,火灾下轻集料混凝土砌块表面会被蒸发的水汽覆盖,从而导致产生一个隔热层,减少λ;温度高于800 ℃后,λ趋于稳定,其规律与EN1994-1-2[13]给出的曲线一致。EN 1996-1-2[8]同样给出了粘土材料热λ随温度变化的曲线,考虑到砌体结构多数情况是受力的,在火灾下容易出现破损裂纹,从而使热量容易传导至内部,所以温度升高到200℃后,λ取了一个较大的偏安全值,见图2。(图中相对热传导率系数,为温度T时λT与20 ℃时λ20的比值)

图2 块体热传导率随温度变化曲线Fig.2 Evolution of thermal conductivity of brick versus temperature

2.1.3密度

由于块体中的水分会随着温度的升高而蒸发,故当温度高于100 ℃后,块体的质量会略有下降。Bidoung等[14]试验对比了黏土砖在200 ℃、400 ℃和600 ℃下的质量损失和密度变化,发现黏土砖的质量损失不明显。EN 1996-1-2[8]规定在进行构件温度响应分析时,可认为黏土砖和轻集料混凝土砌块的密度与温度无关,取其常温密度值即可。

2.2 高温下砂浆的热工性能

高温下砂浆比热的变化趋势与块体有许多相似之处,而热传导率则有所不同,砂浆内部水分的蒸发同样是影响砂浆热工性能的重要因素,砂浆受热发生的物理化学反应也使砂浆的热工性能随温度上升而变化。

2.2.1比热c

图3 砂浆比热随温度变化曲线Fig.3 Evolution of heat capacity of mortarversus temperature

2.2.2热传导率λ

Nguyen等[9-10]也对高温下砂浆的热传导率进行过试验研究,发现在温度小于100 ℃时,λ几乎没有变化;当温度在100 ℃～200 ℃时,λ开始持续下降,下降至原数值的80%;随着温度继续上升,λ继续下降,但下降速率缓慢,最终趋近原数值的50%～60%,如图4所示。

图4 砂浆热传导率随温度变化曲线Fig.4 Evolution of thermal conductivity of mortarversus temperature

2.2.3密度

由于砂浆中自由水分的蒸发,当温度超过100 ℃后,砂浆的密度会略有减少,一般减少50～100 kg/m3。EN 1996-1-2[8]认为在进行构件温度响应分析时,可认为砂浆的密度与温度无关,取其常温密度值即可。

3 砌体结构的高温力学性能

一般来说,砌体的高温力学性能指标主要有抗压强度、抗剪强度、弹性模量和应力-应变关系等,各项性能随温度升高,都有不同程度的劣化,最终都接近衰竭,难以再加利用。

本节结合国内外现有的规范、试验和理论研究等,从高温下和高温冷却后两方面介绍砌体结构的力学性能。为便于对各研究成果之间的数据进行整理和比较,本节对重要参数进行统一的符号规定,详见表1。

表1砌体结构的重要参数符号表

Table 1Significant parameters of masonry

注:表中符号在T温度下的属性,增加下标“T”即可

3.1 抗压强度

尽管国内外对砌体的高温抗压强度进行了很多的研究,但是其结果往往都会有所差异,使得目前国内外并未形成一个统一的公式,更多的是对试验数据的处理,从而给出强度的折减系数。另外高温下构件力学参数的量测对设备要求较高,所以国内学者多数进行了高温冷却后的抗压强度试验研究。

3.1.1高温下的抗压强度

Fu等[17]和Djaknoun等[18]通过研究分别给出了不同成分的水泥砂浆抗压强度随温度变化的曲线;Nguyen等[6]、Ayala[3]和EN 1996-1-2[8]研究给出了块体抗压强度随温度变化的曲线,详见图5。研究发现,在低温阶段,因为材料成分、试件尺寸、加热条件和环境湿度等因素的不同,会导致抗压强度随温度变化趋势的不一致;当温度超过500 ℃后,抗压强度普遍下降。欧规EN 1996-1-2[8]认为黏土砖的抗压强度随温度上升持续下降,而轻集料混凝土砌块的抗压强度则会有少许上升,待到400 ℃后才开始下降;相比块体,砂浆的抗压强度随温度下降得很快,在300 ℃～400 ℃时几乎下降了50%。

图5 高温下抗压强度随温度变化曲线Fig.5 Variation of compressive strength of different samples under high temperature

3.1.2高温冷却后的抗压强度

高温冷却后的抗压强度,既是高温(火灾)后结构的剩余强度。

影响高温(火灾)冷却后砌体结构剩余强度的因素有很多,除了构成材料自身的特性,主要还包括受热的最高温度、升温速率、加热持续时间和冷却方式等。国内外学者为了揭示高温(火灾)后砌体结构剩余强度的变化规律,分别着手研究了砂浆、块体和整体砌体构件的剩余强度,但由于过多的影响因素和砌体构件构成材料的复杂性,因此国内外并未形成一套成熟的理论计算方法,多是基于对试验的归纳和分析。

商景祥等[19]采用IOS834标准升温曲线,研究了多种砂浆试件在受火不同时间后的抗压强度。研究表明,受火相同时间时,不同种类不同强度的砂浆抗压强度下降程度基本相近,如图6所示。

苗生龙等[4]对不同温度后黏土砖砌体构件的抗压强度进行了试验,得到了黏土砖砌体强度随温度变化的规律,并结合国内现有的黏土砖砌体结构的抗压强度计算公式,给出了对应温度下剩余强度的计算方法,见式(1)。

φ1=-6×10-7T2-0.000 3T+1.002 2

10 ℃≤T≤800 ℃

(1)

式中:φ1为不同温度砖抗压强度的折减系数;φ2为不同温度砂浆抗压强度的折减系数;k1,α和k2为《砌体结构设计规范》(GB 50003—2011)[20]附录B中系数。

图6 砂浆剩余强度随受火时间变化曲线Fig.6 Variation of compressive strength of mortar after fire exposure

Russo等[2]通过细致的试验,研究了黏土砖砌体受热冷却后的力学性能。试验不仅进行了砌体整体构件的力学性能研究,还将构件所用的黏土砖和砂浆进行了力学性能测试,分别得到了各自样本强度随温度变化的曲线,如图7和公式(2)所示。其试验的结果也可以更好地展现材料强度和整体构件强度的关系。

(2)

从图7中可以注意到,砌体构件的剩余承强度在300 ℃时会有所上升,这和砂浆的剩余强度变化趋势是一致的;并且黏土砖砌体构件剩余强度的下降程度,是小于其组成材料黏土砖和砂浆;通过和参考资料的对比,发现砌体构件受热的最高温度和最高温度持续时间都是影响剩余强度的重要因素,但是受热的最高温度对构件的抗压强度劣化起到决定性的作用。

Cülfik等[21]分别研究了受火最高温度(Tmax)、最高温度持续时间(tmax)和升温速率(vT)三个参数对砂浆剩余强度的影响。如图8所示,圆形数据点曲线的参数为基础,分别改变增大tmax或减小vT两个参数,得到三角形和方形数据点曲线。对比后可以发现,更大的tmax或更小的vT都减小了砂浆试件的剩余抗压强度;另外得到了和多数资料一致结论,Tmax对强度劣化的影响最大,tmax次之,vT的影响较小。

图7 试件剩余强度随温度变化曲线Fig.7 Variation of compressive strength of samples after high temperature exposure

图8 砂浆试件抗压强度随温度变化曲线Fig.8 Variation of compressive strength of mortar after high temperature exposure

Karahan[22]对砂浆高温后剩余强度与冷却方式的关系进行了试验研究,发现同升温速率一样,不同的降温速率(通过鼓风控制)对砂浆试件的剩余承载力影响不大,但喷水冷却会造成砂浆强度的明显下降,如图9所示。

3.2 弹性模量

同抗压强度相似,高温(火灾)作用会造成砌体结构的弹性模量变化,水分的蒸发、高温下材料的物理化学反应等都会影响到砌体结构的刚度。

3.2.1高温下的弹性模量

在目前收集到的文献数据中[2-3,8,17,23],砌体结构的弹性模量随着温度上升一般呈下降趋势,详见如图10所示。在力学上最直观的体现就是,块体和砂浆受热后会产生微小的裂纹,造成材料的损伤,降低了其刚度。从图中可以看出砂浆和轻集料混凝土的弹性模量都是随着温度的上升而下降,且下降趋势呈线性。但是对于黏土砖弹性模量随温度变化的情况,EN 1996-1-2[8]和Nguyen等[6]则给出了相互矛盾的曲线。Nguyen等[6]的数据显示在200 ℃～750 ℃时,黏土砖的弹性模量出现了上升,之后开始急剧下降;EN 1996-1-2[8]则给出了黏土砖弹性模量随温度升高而下降的曲线。Russo等[23]认为这应该是由于所使用黏土砖的化学和物理特性不同所造成的,同时黏土砖的烧结温度也会影响其在高温下的弹性模量。

图9 不同冷却方式下砂浆抗压强度随温度变化曲线Fig.9 Variation of compressive strength of cement mortar with different cooling regimes

图10 高温下弹性模量随温度变化曲线Fig.10 Variation of elastic modulus of different samples under high temperature

3.2.2高温冷却后的弹性模量

Russo等[2]对黏土砖砌体构件、黏土砖和砂浆进行了高温冷却后的弹性模量测定,详见图11(a),并根据试验结果归纳了黏土砖砌体构件弹性模量与温度的经验公式(3)。从给出的资料可以看出,黏土砖和黏土砖砌体构件的弹性模量随温度变化的趋势基本一致,在温度低于300℃时,两者受热冷却后的弹模会有一定上升。这一现象在Russo等[24]对古建筑受火后力学性能的研究中也有所体现。但多数国内外文献[5,21,25]显示了黏土砖砌体构件的弹性模量随温度上升而持续下降,如图11(b)所示。

(3)

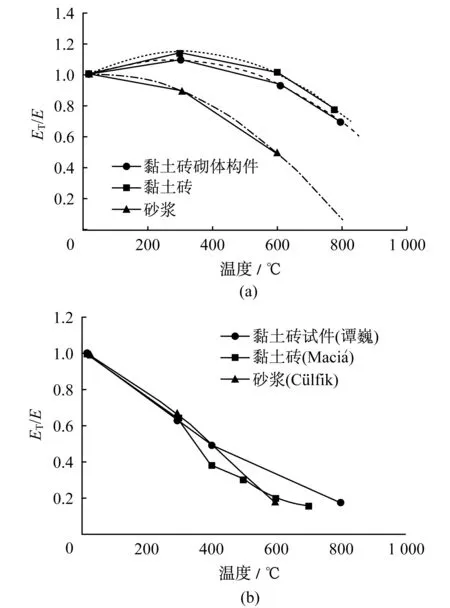
图11 高温冷却后弹性模量随温度变化曲线Fig.11 Variation of elastic modulus of different samples after high temperature

3.3 应力-应变关系

砌体构件在高温下和高温冷却后,虽然抗压强度、弹性模量等力学参数会有所不同(高温冷却后的力学性能会下降得更多[5]),但是均呈脆性破坏。国内外许多学者和机构,都通过研究建立了块体、砂浆和砌体构件在不同温度下的本构模型。

3.3.1高温下的应力-应变关系

现有的研究数据显示:不论在常温还是高温下,黏土砖的应力-应变曲线在上升段(达到峰值应力前)几乎呈线性发展;下降段时应力则迅速降到0,呈现出明显的脆性破坏形式;而轻集料混凝土砌块和砂浆的曲线在上升段均呈非线性[17,26],如图12所示。EN 1996-1-2[8]根据材料脆性破坏的特征,分别给出了粘土砖和轻集料混凝土砌块的本构关系计算模型,如图12(a),(b)所示。Nguyen等[6]通过试验测得的黏土空心砖不同温度下应力-应变上升段曲线,也符合线性增长的规律,很好地验证了EN 1996-1-2提出的黏土砖本构模型,如图12(c)所示。

图12 高温下块体和砂浆受压应力-应变曲线Fig.12 Stress-strain relationships of brick and mortar at different temperatures

3.3.2高温冷却后的应力-应变关系

Russo等[2]、Sciarretta[27]通过多次试验,对不同温度冷却后的黏土砖砌体构件及组成材料进行了力学研究。试验数据显示:①即使加热温度只有300 ℃,应力-应力的曲线也发生了一定的变化;②不同温度的应力-应变曲线在上升段的变化并不明显,而在下降段则有显著的区别,如图13所示。当应力下降到峰值应力的一半时,不同温度冷却后对应的极限应变差距很大,300 ℃和600 ℃的极限应变分别比常温下增加了51%和158%;③同样也可以从图中看出高温冷却后构件抗压强度和弹性模量的下降,尤其是在600 ℃时。

Sciarretta[27]又在上述两人试验研究的成果上,总结出图13的本构关系表达式,分为初始弹线性上升段、非弹性上升段和下降段,σ-ε关系见式(4)-式(6)。

图13 不同温度冷却后的应力应变关系曲线Fig.13 Residual constitutive law for masonry after high temperature exposure

①线弹性上升段0≤ε≤εc0,T:

(4)

②非弹性上升段εc0,T≤ε≤εc,T:

(5)

③下降段εc,T≤ε≤εc2,T:

(6)

4 展 望

综上所述,国内外学者已经对砌体结构的高温热工性能(包括比热、热传导率和密度)和高温力学性能(抗压强度、弹性模量和应力-应变关系)进行了大量研究,取得了一定成果,但并未形成统一的计算方法,各方试验结果离散性较大且部分相互矛盾,所以仍需深入研究。

(1) 热工性能方面:高温下砌体材料的比热和密度呈现出很好的规律性,影响其变化的主要因素为100 ℃左右时材料内部水分的蒸发。与之相反,砌体材料的热传导率随温度变化的关系则没有一个统一趋势,所以仍需进行更深入的研究,以确定影响其数值大小的决定因素。

(2) 力学性能方面:总体来说,随着温度的上升,砌体结构的力学性能均趋于降低,但不同类型砌体材料的下降过程又各有不同。随着各种类型多孔砖和新型材料砖体的广泛应用,目前的研究成果已经无法满足砌体结构发展的需要,所以本文在此给出砌体的高温力学性能研究状态,见表2,为今后的砌体结构高温力学性能研究提供思路和参考。

表2高温下和高温冷却后砌体力学性能研究状态

Table 2Research status of mechanical properties of masonry under or after high temperature

注:“*”表示欧规EN 1996-1-2[28]中提供了高温下砂浆、轻集料混凝土砌块和黏土砖的抗压强度、弹性模量和应力-应变关系等数据