隔震结构系统线性黏弹性液体阻尼器非平稳响应分析法

李创第，柏大炼，葛新广，刘 鹏

(广西科技大学 土建学院，广西 柳州 545006)

目前，橡胶支座基础隔震等减震技术已广泛应用于国内外的实际工程[1]，振动频率对橡胶隔震支座的阻尼和有效刚度影响较大[2-4]。建筑结构设置隔震层之后，通常还需在隔震层增设黏弹性液体阻尼器来限制隔震层的过大位移[5]，这将导致隔震结构的频率依赖特性更加突出。随着高层隔震技术的不断发展[6]，普通橡胶支座目前常用的线性黏滞阻尼分析模型已不能充分表征振动频率对结构响应的影响，各种基于线性黏弹性本构关系的橡胶支座的分析模型已被提出[7-8]。此外，考虑频率影响的橡胶支座的非线性分析模型也被提出[9]。由于实际地震动具有非平稳随机特性，且作为隔震结构保护装置的消能减震构件(支座和阻尼器)的受力性能对隔震结构的整体安全性有重大影响，如2011年3月11日发生在日本东北近海地震中，消能减震构件的损伤和破坏均加剧了消能减震主体结构的损伤和破坏[10]。因此我国《建筑抗震设计规范》和《建筑消能减震技术规程》[11]均明确要求消能减震构件在结构设计基准期内应具备足够的抗震可靠度和良好的变形与耗能能力，故建立黏弹性阻尼器合理的抗震分析与设计方法是非常有必要的。

线性黏弹性阻尼器已广泛用于各种土木结构的被动控制，然而对于抗震结构，国内外均采用基于模态叠加法的反应谱设计法，由于黏弹性耗能结构的模态不具正交性，黏弹性阻尼器的振动机理及其与耗能主体结构振动机理的相互关系仍不清楚，现有的分析法无法将黏弹性阻尼器和耗能主体结构的响应精确分解为各模态响应的线性组合，导致黏弹性阻尼器和耗能主体结构精确的抗震反应谱设计法无法建立，因此黏弹性减振控制的实用设计理论及其在规范的应用已被列为我国土木结构振动控制领域近期需要深入研究的关键科学问题之一[12]。

具有记忆和频率依赖特性的线性黏弹性阻尼器、支座和材料[13-15]的现有计算模型分为4类，即复模量模型及其近似[16-17]；一般微分模型及其近似[18-20]；分数导数模型[21-23]；一般积分型模型[24-27]。其中一般积分型模型是最一般的模型，其余模型均为该模型的近似或无限逼近。

线性黏弹性耗能结构的现有解析法分为扩阶精确法和非扩阶近似法两类。

扩阶精确法针对广义Maxwell和Golla等[28]、分数导数Kelvin等易扩阶的近似模型，用扩阶复模态法获得解析解。因扩阶方程组物理意义不够明确，变量个数剧增，计算效率低，使该方法的实际应用受到限制。研究表明：广义Maxwell模型和分数导数模型具有相互等效性[29]，且广义Maxwell模型对黏弹性本构关系的试验拟合精度较分数导数模型高[30]。因基于分数导数模型的时域脉冲响应函数是Mittag-Leffler特殊函数的线性组合，不仅计算复杂，而且无法与工程抗震设计反应谱建立直接对应关系，故在工程抗震分析中，有关文献建议不采用该模型。

非扩阶近似法主要是模态应变能法和强行振型解耦法。因近似法采用复模量频域建模方式，不能严格适用于非简谐激励的时域分析，且仅为一阶小量近似，并采用了较多的近似假设，使其精度和适用范围受到限制[31]。

关于线性黏弹性耗能结构随机响应分析，目前应用扩阶复模态法，已获得广义Maxwell阻尼耗能多自由度结构在平稳滤过白噪声激励下的平稳响应解析解[32-34]和Maxwell阻尼耗能多自由度结构在Shinozuka型均匀调幅滤过白噪声激励下的非平稳响应解析解[35]。然而对于一般线性黏弹性耗能结构在平稳和非平稳滤过白噪声激励下的平稳与非平稳响应分析法尚未建立。

关于线性黏弹性阻尼器的响应分析，尽管阻尼器受力分析的重要性早已形成共识[36-40]。但由于分析的复杂性，目前仅获得线性黏弹性耗能单自由度结构在简谐荷载激励下一般黏弹性阻尼器稳态响应的解析解，尚未获得黏弹性耗能结构在任意荷载激励下一般黏弹性阻尼器瞬态响应的解析解。

经典虚拟激励法已广泛应用于未设置黏弹性阻尼器结构的非平稳随机响应的高效分析[41]，然而该法在每个离散频点处都涉及到虚拟激励作用下运动方程的时程积分，对于大型结构，其计算量仍相当大。为此，文献[42-43]将经典结构动力方程转化为状态方程形式，通过建立任意离散时刻经典结构响应关于时间截口随机激励的显示线性表达式，建立了计算效率更高的快速虚拟激励法，并将该法成功应用于经典非线性结构非平稳响应的快速等效线性化分析[44]；然而目前的快速算法仅针对均匀调幅非平稳随机激励作用下的经典结构，尚未考虑非均匀调幅非平稳随机激励和设置阻尼器的耗能结构，且算法涉及到指数矩阵和相关逆矩阵的计算，从而使该算法的适用范围受到限制。

传递矩阵法的最大优点是不需扩阶，可直接获得一般线性黏弹性耗能对称结构瞬态响应的非扩阶解析解。本文采用一般积分型黏弹性分析模型，将传递矩阵法应用到一般线性黏弹性耗能非对称结构。在获得一般线性黏弹性液体阻尼器在任意激励作用下瞬态响应非扩阶模态叠加精确解的基础上；应用此解析解和快速虚拟激励法，通过建立任意离散时刻隔震系统及其一般线性黏弹性液体阻尼器响应关于时间截口随机激励的显示线性表达式，建立隔震系统及其阻尼器在均匀与非均匀调幅滤过白噪声地震激励下非平稳响应的快速分析法，并使分析法不需要进行矩阵求逆计算；为建立线性黏弹性阻尼器基于模态叠加的抗震反应谱设计法以及抗震非平稳可靠度分析法提供分析路径；同时，也为建立考虑频率影响的非线性隔震结构在非平稳地震激励作用下非平稳响应的等效线性化分析法提供分析基础。

1 结构运动方程

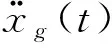
(1)

(2)

(3)

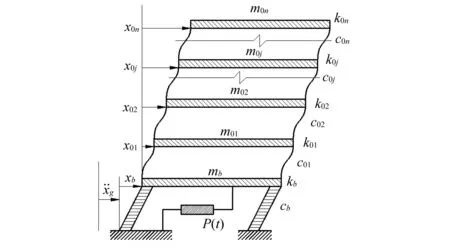
图1 结构计算简图Fig.1 Structural calculation diagram

对于一般线性黏弹性液体阻尼器P(t)，其平衡刚度kp=0。当仅考虑线性隔震支座的频率依赖性质时，可用P(t)表示黏弹性隔震支座的本构关系，此时，取kb=0，cb=0；故在一般积分型本构关系中，仍保留kp，以便使式(1)～式(3)更具广泛适用性，只是在具体计算液体阻尼器P(t)的响应时，取kp=0进行计算。

将位移向量x0按上部结构的前N,(N≤n)个振型展开，即

(4)

则式(1)和式(2)可化为非对称微分—积分方程组

(5)

其中，

x=[x1,x2,,xm]T=

[x1,x2,xN,xb]T,(m=N+1)

(6a)

(6b)

C=diag[2ξ01ω01,,2ξ0Nω0N,2ξbωb]

(6c)

(6d)

(6e)

r=[r1,,rm]T=[r1,，rN,1]T

(6f)

(6g)

(6h)

式中：mi,ξ0i，ω0i,ri,(i=1～N)分别为振型φi对应的广义质量、阻尼比、圆频率和振型参与系数。

2 结构系统特征值和传递矩阵

2.1 结构特征值和特征向量分析

设结构的初始条件为

(7)

对式(5)取拉氏变换，可得

(8)

(9)

(10)

结构特征值方程为

det[D(s)]=0

(11)

(12)

式中：qk(s)和qk-1(s)分别为s的k次和次k-1多项式函数。

由式(11)可求出结构的M个特征值sj。每个特征值sj对应的结构右、左特征向量(模态)uj和vj，可由下列特征向量(模态)方程求出

(13)

式中：j=1～M。

2.2 阻尼器特征值和特征向量分析

将阻尼器P(t)的本构式(3)表示为

P(t)=LTg(t)

(14a)

(14b)

式中：L=[0 0 1]T，也即xb=LTx。

对式(14)取拉氏变换，并考虑关系式(8)，可得

(15a)

(15b)

故阻尼器的变换向量g(t)的传递矩阵Hg(s)和阻抗矩阵Dg(s)分别为

(16a)

(16b)

(16c)

由阻尼器P(t)的实际物理意义和其本构关系式(3)知：P(t)≠0；故

(17)

也即

(18)

故阻尼器的变换向量g(t)的特征值方程为

(19)

由式(18)和式(19)知：g(t)的特征值与结构位移x(t)的特征值完全相同。g(t)的每个特征值sj对应的右、左特征向量ugj和vgj，可由下列特征向量方程求出

(20a)

(20b)

式中：j=1～M。

对比式(13)和式(20)，可得g(t)与x(t)的特征向量的对应关系为

(21a)

(21b)

2.3 结构传递矩阵解析式

由于结构特征值sj是结构传递矩阵的极点，故根据残数理论，按照文献[45]类似的方法(详见附录A)，可求得结构传递矩阵的解析式为

(22a)

(22b)

其中，

(23a)

(23b)

2.4 阻尼器变换向量的传递矩阵解析式

将g(t)的传递矩阵Hg(s)按其特征值sj展开，按照文献[45]类似的方法(详见附录B)，可求得g(t)的传递矩阵的解析式为

(24a)

(24b)

3 阻尼器和结构时域瞬态响应解析解

3.1 阻尼器瞬态响应解析解

由式(15a)、式(16a)和式(24a)、式(10)，可得

(25)

对式(25)取拉氏逆变换，得

(26)

式中：δ(t)为Dirac delta函数。

对于t>0，阻尼器受力响应可进一步表示为

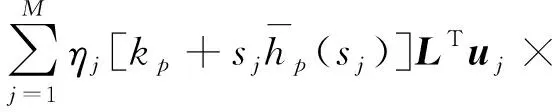
(27)

式中：aj(t)为初始条件产生的响应

(28)

显然，对于零初始条件，aj(t)=0，(j=1～M)。

同理，由式(15a)、式(16a)和式(24b)、式(10)，可得t>0时的阻尼器受力速率响应解析解为

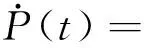
(29)

3.2 结构位移与速度瞬态响应解析解

同理，由式(8)、式(10)和式(22)，可得t>0时的结构位移和速度瞬态响应解析解分别为

(30a)

(30b)

3.3 结构系统地震响应解析式

由于所有用于工程实际的随机非平稳地震激励模型均为零初始条件，由式(27)、式(29)、式(30)和式(6h)，在零初始条件下，结构广义位移、速度和阻尼器受力、受力速率响应分别为

(31)

(32)

(33)

(34)

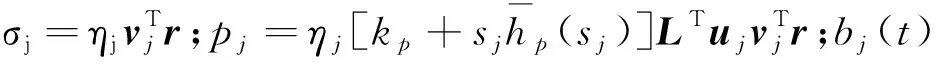
(35)

(36)

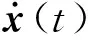
(37)

由式(31)～式(34)和式(36)、式(37)，原始结构的位移、速度和阻尼器等响应S(t)均可统一表示为

(38)

4 隔震结构系统非平稳响应

4.1 非平稳地震激励模型

本文针对统计特性随时间变化，但经过足够长时间后趋于平稳态的非平稳随机地震激励，采用Priestley提出的演变谱模型[46]，它可以表示为

(39)

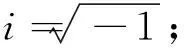
4.2 结构系统非平稳响应表达式

由式(38)知，结构系统一般响应S(t)的非平稳协方差函数的表达式为

(43)

4.3 非平稳响应特性分析的虚拟激励法

将式(41)代入式(43)得

(44)

式中：Yj(ω，t)为标准一阶系统对激励a(ω,t)eiωt的响应，即

(45)

(46)

根据虚拟激励法，若构造虚拟激励

(47)

则由标准一阶系统式 (45) ，产生的虚拟响应必为

(48)

由式(48)和式(44)可得

由式(45)～式(48)知

(50)

对式(50)取时间步长Δt=ti+1-ti，进行数值离散化得

(51)

式中：T=esjΔt。

在很小的时间步长Δt内，通常可以认为激励是线性变化的，则式(51)可表示为

(52)

其中，

(53)

(54a)

T0Q3f(ti-1)+Q2f(ti),i≥2

(54b)

其中，

Q3=TQ2+Q1

(55)

式中:f(t0)，f(t1),,f(ti)的系数若用Ai,0,Ai,1,,Ai,i表示，则式(54)可表示为

令

Wi=[Ai,0Ai,1Ai,i]

(57)

Ji=[f(t0)f(t1)f(ti)]T

(58)

则式(56)可进一步表示为

(59)

ti时刻的系数Ai,0,Ai,1,,Ai,i只和结构有关，且可用ti-1时刻的系数Ai-1,0,Ai-1,1,,Ai-1,i-1表示。

(60a)

(60b)

(60c)

根据式(60)建立各时刻对应的系数如表1所示。

表1 各时刻对应的系数Tab.1 Corresponding coefficients at each moment

由表1可知，为了得到各时刻对应的系数，仅需计算f(t0)和f(t1)所对应的2列，即Ai,0和Ai,1。且不需求逆计算，因此，可使计算更为高效。

式(61)的积分为无穷广义积分，可按文献[41-43]提出的方法计算。

5 算 例

5.1 多层隔震系统解析解的验证分析

5.1.1结构系统方程

对于40 m以下的多层隔震结构，相对位移向量x0可按上部结构第一振型φ1及其广义坐标x1(t)展开，即

x0=φ1x1(t)

(62)

此时，隔震结构系统方程式(5)可化简为

(63)

(64)

其中，

x=[x1,x2]T=[x1,xb]T;r=[r1,r2]T=[r1,1]T(65)

(66)

(67)

5.1.2验证算例1：Maxwell阻尼隔震系统解析解分析

对于Maxwell阻尼隔震结构，可用本文方法和复模态法求解，下面比较两种方法结果。

对于Maxwell阻尼器P(t)，其松弛函数简化为

(68)

(69)

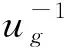
5.1.2.1 本文方法

由式(11)和式(13)，结构系统的特征值和特征向量方程分别为

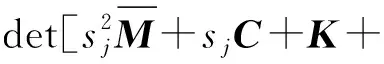
(70)

D(sj)uj=0;D(sj)Tvj=0

(71)

由以上两式，可求得结构系统的5个特征值sj及其对应的5个右、左特征向量uj，vj,j=1～5。

由式(23)，可求得计算参数ηj为

(72)

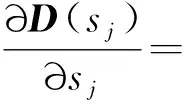
(73)

由式(31)和式(33)，在零初始条件下，结构系统响应为

(74)

5.1.2.2 复模态法

(1)结构系统扩阶方程

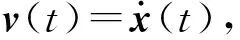
(76)

(77)

(78)

其中，

(79)

故结构系统扩阶状态方程为

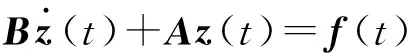
(80)

其中，

(81)

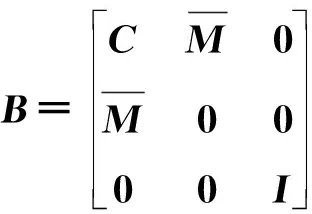
(82)

(83)

式中：0,I分别为2×2阶零矩阵和单位矩阵。

(2)结构系统特征值和特征向量分析

令

x=xjeλj t

(84)

(85)

R=Rjeλj t

(86)

则结构系统右模态方程为

[Bλj+A]Φj=0

(87)

(88)

展开上式得

(89)

(90)

(91)

由式(91)，将Rj用xj表出，并代入式(89)，可得

(92)

(93)

对比式(70)、式(71)和式(93)知，λj=sj，xj=uj，j=1～5。故结构系统的特征值为sj，相应的右特征向量Φj为在式(88)和式(92)中，令λj=sj，xj=uj可得。

结构系统左模态向量方程为

[Bsj+A]TΨj=0,j=1～5

(94)

令

(95)

展开上式得

(96)

(97)

[LLT]Tyj+(sj+ug)χ1j=0

(98)

由式(97)和式(98)，将χ1j和χ0j用yj表出，并代入式(96)，可得

(99)

(100)

(101)

对比式(70)、式(71)和式(101)知，yj=vj，故结构系统的特征值为sj，j=1～5，相应的左特征向量Ψj为在式(95)、式(99)和式(100)中，令yj=vj可得。

(102)

(3)结构系统响应分析

由复模态法[47]，在零初始条件下，结构位移响应为

(103)

(104)

故结构系统响应x(t)和R(t)为

(105)

(106)

(4)阻尼器响应分析

由式(64)和式(68)，阻尼器P(t)的响应为

(107)

由于,

(108)

将式(108)代入式(107)，可得

P(t)=kpLTx+M0LTR

(109)

将式(105)和式(106)代入式(109)，可得

(110)

对比式(74)、式(75)和式(105)、式(110)可知，本文方法和复模态法结果完全相同。

5.1.3验证算例2：结构系统频率响应函数分析

5.1.3.1结构系统频率响应函数解析式

由式(31)和式(33)，在零初始条件下，结构系统响应的精确解为

(111)

式中：sj,ηj,uj,vj由式(11)、式(13)、式(23)计算。

由式(111)和式(112)，结构系统的脉冲和频率响应函数分别为

(113)

(114)

(115)

(116)

而直接由结构系统方程(63)和式(64)获得的频率响应函数为

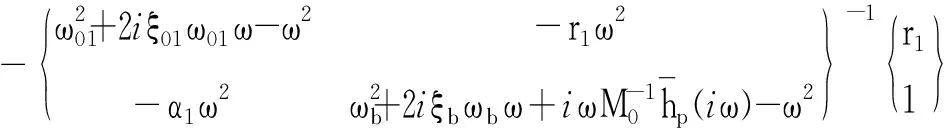
(118)

由于本文方法所得的频率响应表达式式(115)、式(116)和结构系统方程直接所得的频率响应表达式式(117)、式(118)均为解析解，故应相等。

5.1.3.2 验证算例2

某8层框架隔震结构，上部结构层间质量m01～m02为300×103kg，m03～m08为270×103kg；层间刚度k01～k02为4×105kN/m，k03～k08为3.5×105kN/m；上部结构第一阵型阻尼比ξ1=0.05。隔震层质量mb为410×103kg，隔震层等效圆频率ωb为5.27 rad/s，等效阻尼比为ξb分别为0.10,0.15,0.2,0.25。

隔震层设置线性黏弹性液体阻尼器P(t)，平衡刚度kp=0 kN/m；松弛函数hp(t)的拉氏和傅氏变换取二次分式

其计算值取为ωp=9.45 rad/s；d1=28.4 rad/s；e1=65 rad/s；e2=950 rad/s。

图2～图4分别为按本文方法和结构系统方程直接获得的频率响应表达式的计算结果。由图可知，本文方法和方程求解的结果完全相同，从而验证了本文方法的正确性。

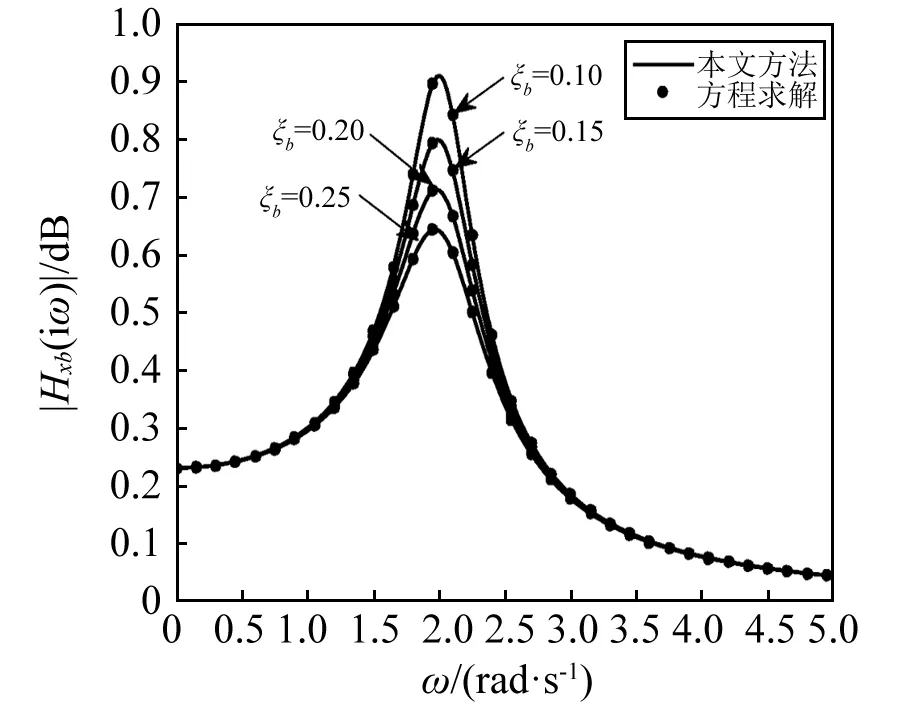
图2 隔震层频率响应函数模 |Hxb(iω)|Fig.2 Calculation values of |Hxb(iω)| of isolated layer frequency response function

图3 上部结构频率响应函数模|Hx1(iω)|Fig.3 Calculation values of |Hx1(iω)| of the upper structure frequency response function

图4 阻尼器受力频率响应函数模|Hp(iω)|Fig.4 Calculation values of |Hp(iω)| of damper’s force frequency response function

5.2 算例3：隔震结构系统非均匀调幅地震响应分析

某10层框架隔震结构，上部结构参数如表2所示；结构第一阵型阻尼比ξ1=0.05。隔震层质量mb为375×103kg，隔震层等效圆频率ωb为18 rad/s，等效阻尼比为ξb为0.20，数值离散时间步长Δt=0.02 s。

隔震层设置线性黏弹性液体阻尼器P(t)，平衡刚度kp=0 kN/m；松弛函数hp(t)的拉氏和傅氏变换取二次分式

其计算值取为ωp=[5.4 7.3 8.1 10.5] rad/s;d1=31.3 rad/s;e1=61.90 rad/s;e2=952.24 rad/s。

表2 耗能隔震结构的上部结构参数Tab.2 The upper structural parameters of energy dissipation isolated structure

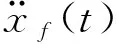
其计算取值为：ωf=10.9 rad/s，ξf=0.96；S0=0.015 54 m2/s3。

调幅函数a(ω,t)分别取为Shinozuka-Sato型[48]均匀调幅和Spanos-Solomos型[49]非均匀调幅函数，计算参数取为

在Shinozuka-Sato型均匀调幅非平稳地震激励作用下，隔震层、上部结构第五层及顶层的层间位移与速度响应方差如图5～图10所示；液体阻尼器P(t)的受力响应方差如图11所示。

在Spanos-Solomos型非均匀调幅非平稳地震激励作用下，隔震层、上部结构第五层及顶层的层间位移与速度响应方差如图12～图17所示；液体阻尼器P(t)的受力响应方差如图18所示。

由计算结果可以看出：阻尼器受力响应对隔震结构系统响应影响较大；ωp越大，也即设置阻尼器越多，则阻尼器总的受力响应方差越大，结构的系统响应方差越小，也即减震效果越好。

图5 Shinozuka-Sato型调幅函数 下隔震层位移响应方差Fig.5 Variance of displacement response of isolation layer with Shinozuka-Sato amplitude modulated function

图6 Shinozuka-Sato型调幅函数下 第五层层间位移响应方差Fig.6 Variance of relative displacement response of fifth layer with Shinozuka-Sato amplitude modulated function

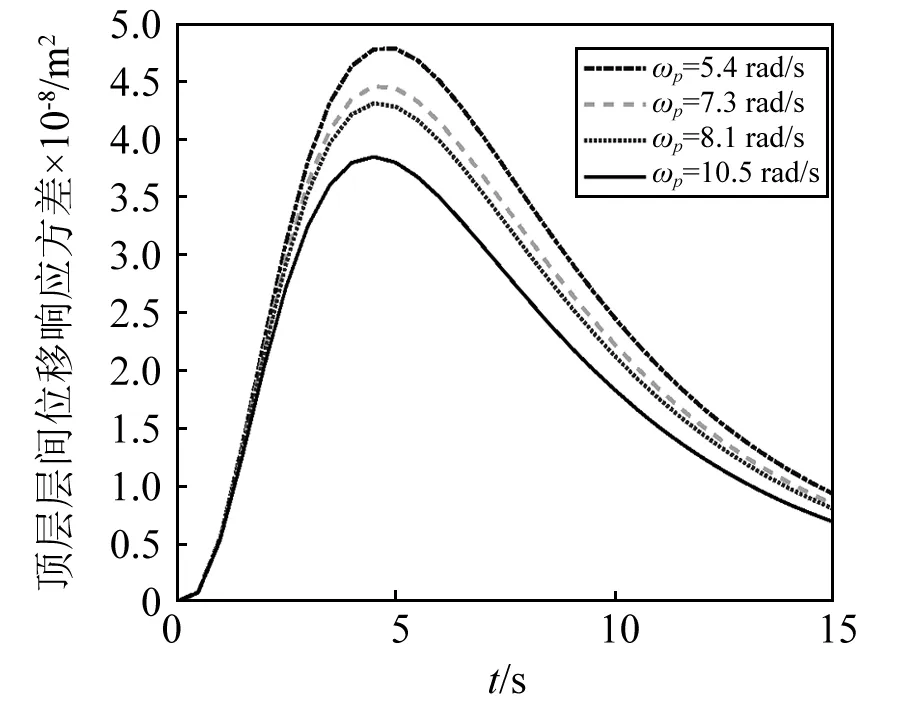
图7 Shinozuka-Sato型调幅函数下 顶层层间位移响应方差Fig.7 Variance of relative displacement response of top layer with Shinozuka-Sato amplitude modulated function

图8 Shinozuka-Sato型调幅函数下 隔震层速度响应方差Fig.8 Variance of velocity response of isolation layer with Shinozuka-Sato amplitude modulated function

图9 Shinozuka-Sato型调幅函数下 第五层层间速度响应方差Fig.9 Variance of relative velocity response of fifth layer with Shinozuka-Sato amplitude modulated function

图10 Shinozuka-Sato型调幅函数下 顶层层间速度响应方差Fig.10 Variance of relative velocity response of top layer with Shinozuka-Sato amplitude modulated function

图11 Shinozuka-Sato型调幅函数下 隔震层阻尼器受力响应方差Fig.11 Variance of isolation layer damper’s response force with Shinozuka-Sato amplitude modulation function

图12 Spanos-Solomos型调幅函数下 隔震层位移响应方差Fig.12 Variance of displacement response of isolation layer with Spanos-Solomos amplitude modulated function

图13 Spanos-Solomos型调幅函数下 第五层层间位移响应方差Fig.13 Variance of relative displacement response of fifth layer with Spanos-Solomos amplitude modulated function

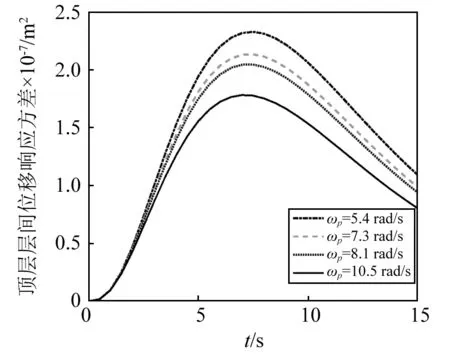
图14 Spanos-Solomos型调幅函数下 顶层层间位移响应方差Fig.14 Variance of relative displacement response of top layer with Spanos-Solomos amplitude modulated function

图15 Spanos-Solomos型调幅函数下 隔震层速度响应方差Fig.15 Variance of velocity response of isolation layer with Spanos-Solomos amplitude modulated function

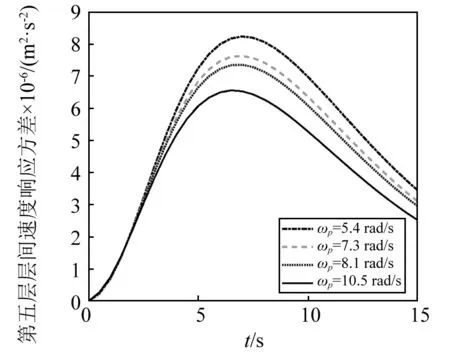
图16 Spanos-Solomos型调幅函数下 第五层层间速度响应方差Fig.16 Variance of relative velocity response of fifth layer with Spanos-Solomos amplitude modulated function

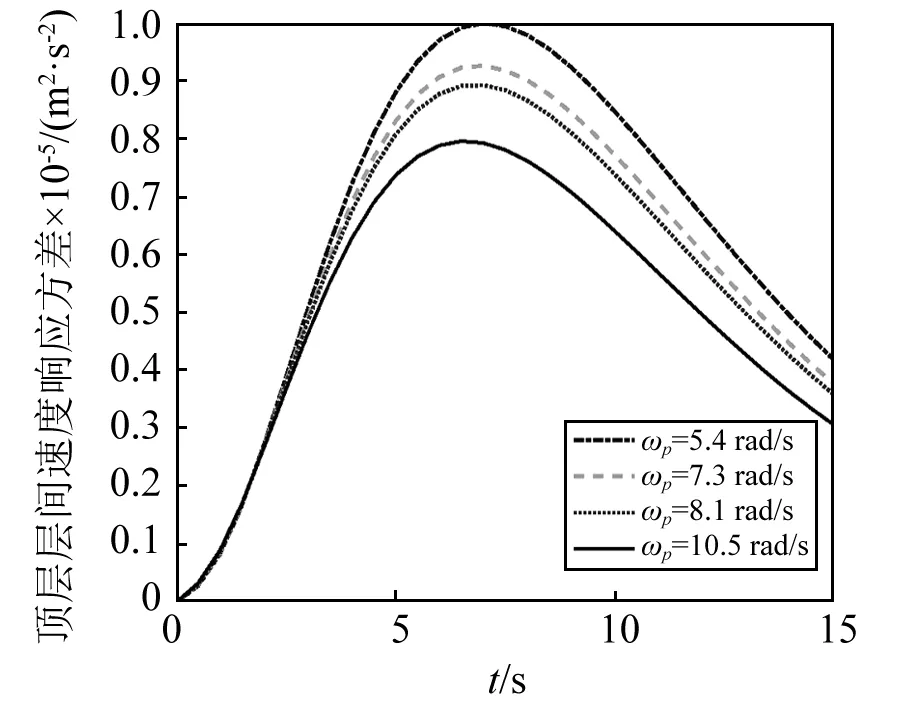
图17 Spanos-Solomos型调幅函数下 顶层层间速度响应方差Fig.17 Variance of relative velocity response of top layer with Spanos-Solomos amplitude modulated function

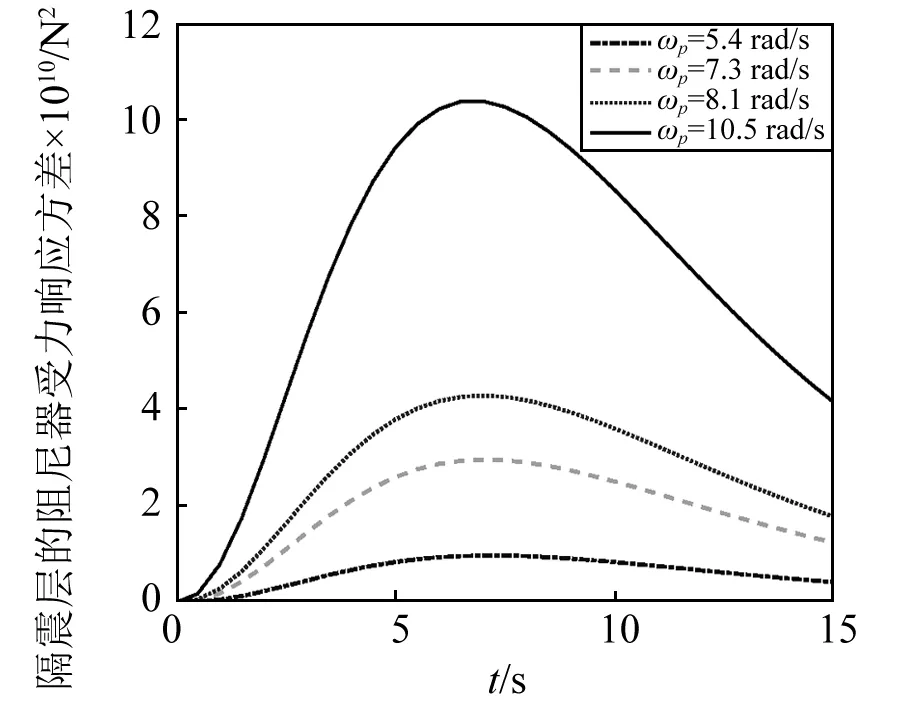
图18 Spanos-Solomos型调幅函数下 隔震层阻尼器受力响应方差Fig.18 Variance of isolation layer damper’s response force with Spanos-Solomos amplitude modulation function

6 结 论

为建立线性黏弹性阻尼器抗震动力可靠度分析法和基于反应谱的模态叠加抗震设计法，对隔震结构系统一般线性黏弹性液体阻尼器时域瞬态响应的模态叠加解析解和非平稳随机地震响应分析法进行了系统研究，获得了摘要所述结果。所获得的结构整体系统(含阻尼器)的时域瞬态响应解析解具有明确物理意义，可视为现有黏滞阻尼非对称定常结构的经典模态叠加解析解在线性非对称频率依赖结构的推广，能揭示频率依赖系统的振动机理，即频率依赖结构系统的瞬态响应分析，归结于其特征值和对应特征向量(模态)的分析；尽管频率依赖耗能结构的模态不具有正交性，耗能结构方程不能用模态解耦，但耗能结构系统的各种响应(含结构位移、速度和阻尼器受力、受力速率)仍然可精确表示为物理意义明确的结构各模态响应的线性组合。此振动机理可为建立非对称频率依赖耗能结构整体系统的精确模态分解反应谱设计法提供分析路径。

所建立的整体隔震系统的一般非平稳随机地震响应(含结构位移、速度和阻尼器受力、受力速率)分析法可直接应用于隔震结构系统各构件基于泊松过程法的抗震动力可靠度分析；同时，也为建立考虑频率影响的非线性隔震结构在非平稳地震激励作用下非平稳响应的等效线性化分析法提供分析基础。

(A1)

(A2)

式中：adj[D(s)]为D(s)的伴随矩阵。

由正文式(11)，有

D(sj)adj[D(sj)]=adj[D(sj)]D(sj)=

Idet[D(sj)]=0

(A3)

式中：I为m阶单位矩阵。比较正文式(13)和式(A3)，得

(A4)

式中：j=1～M；ai,bi均为常数。令

uj=[u1j,u2j,,umj]T

(A5)

从式(A4)知，伴随矩阵adj[D(sj)]的每行各元素之比相等，即

(A6)

也即

(A7)

bi=kjuij,(i=1～m)

(A8)

式中：kj为比例常数，j=1～M。

将式(A8)代入式(A4)，得

(A9)

将式(A9)代入式(A2)，得

(A10)

(A11)

式中：j=1～M；ηj为常数。

下面求出ηj的表达式。由式(A1)和式(A10)，有

(A12)

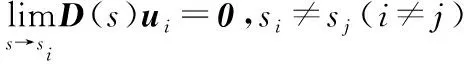
(A13)

故有

ηi=1/γi

(A14)

(A15)

(A16)

式中：γi为常数；i=1～M；式(A16)由正文式(9)得出。

由式(A1)和式(A10)，H(s)的解析式为

(A17)

式中：常数ηj由式(A14)～式(A16)计算。

由式(A1)和式(A2)，sH(s)的解析式为

(A18)

(A19)

将式(A19)和式(A10)代入式(A18)，可得

(A20)

附录B：g(t)传递矩阵Hg(s)解析式的推导

由于在附录A的推导中，对结构位移动刚矩阵D(s)和其逆矩阵(亦称传递矩阵)D(s)-1=H(s)的具体形式未作任何假设；故解析式(A17)和式(A20)具有普遍性，也即：任意动刚矩阵D(s)的逆矩阵D(s)-1=H(s)和sH(s)均可通过动刚矩阵D(s)的特征值和特征向量解析表示，即

(B1)

(B2)

(B3)

式中：sj,uj和vj分别是动刚矩阵D(s)的特征值和相应的特征向量，也即

det[D(sj)]=0,(j=1～M)

(B4)

(B5)

由于解析表达式(B1)～式(B3)对具有实际物理意义的任意动刚矩阵D(s)均成立。故对于g(t)的传递矩阵Hg(s)和sHg(s)，下列解析式均成立

(B6)

(B7)

(B8)

式中：sj是g(t)的动刚矩阵Dg(s)的特征值，其值与结构位移x(t)的动刚矩阵D(s)的特征值完全相同；ugj和vgj分别是动刚矩阵Dg(s)对应于特征值sj的右、左特征向量。

由正文式(16c)，可得

(B9)

将式(B9)代入式(B8)，可得

(B10)

将正文式(21)关于ugj和vgj的表达式代入式(B10)，可得

(B11)

由于uj是D(s)对应于特征值sj的右特征向量，故D(sj)uj=0，代入关系式(B3)，式(B11)可化简为

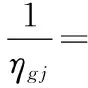
(B12)

也即

(B13)

将正文式(21)和式(B13)代入式(B6)、式(B7)，最终可得

(B14)

(B15)