非高斯噪声环境下的稀疏自适应滤波算法研究*
2019-01-23侯威翰
侯威翰,郭 莹
(沈阳工业大学 信息科学与工程学院,辽宁 沈阳 110870)
0 引 言
目前,自适应滤波已经被广泛应用于各种工程,如声学通信中的回声消除系统、无线通信中的多径信道、水下通信和信道估计[1]等。但是,在实际应用中,存在两个影响算法正常工作的主要因素。
首先是稀疏系统。稀疏信道广泛存在于自然界,如水下通信的信道。稀疏信道的特点是大部分信道的系数都为零或逼近于零,只有很少部分的信道系数为正常值。具备这种特点的信道会给自适应滤波算法带来严重影响。为了解决这个问题,研究者提出了很多具有针对性的方法,如成比例的归一化最小均方算法(PNLMS)[2]。此种算法通过引入比例系数矩阵,改善固定步长的算法在对每个滤波器抽头系数分配步长时出现的不合理现象。比例矩阵可以对每一个滤波器抽头系数分配到的步长进行二次合理分配,从而避免在为零或者趋近于零的信道点处浪费较大的步长值。但是,这种算法在计算时收敛速度较慢。为了在解决稀疏信道的同时改善算法的收敛速度,一种成比例的仿射投影算法被提出(PAPA)[3]。仿射投影算法建立在归一化最小均方算法(NLMS)上,引入了数据重用方法,通过输入数据的瞬时均值来代替统计均值的方法。这种算法的收敛速度要高于归一化最小均方算法,代价是增大了算法的计算复杂度。但是,单纯引入成比例系数矩阵的算法在实际应用中效果并不理想,因为传统的系数比例矩阵对信道的稀疏度要求很高,只能应用于非常稀疏的系统。但是,实际应用中,信道的稀疏度往往是不固定的,所以需要一种可以适应任意稀疏度的自适应滤波算法。文献[4]在PAPA的基础上提出了一种改进的成比例仿射投影算法(IPAPA)。这种改进的比例系数矩阵可以进一步合理分配每个滤波器抽头系数的步长,从而可以适应各种不同类型的稀疏信道,使自适应滤波算法在保证收敛速度的同时摆脱信道稀疏度的限制。
其次,非高斯噪声。非高斯噪声同样普遍存在于自然界,如图像处理中的椒盐噪声、电气开关开启瞬间产生的脉冲噪声、潮汐或者地震等自然现象在水中产生的噪声等。这些非高斯噪声同样会给自适应滤波算法带来严重破坏,尤其是基于二阶统计量的自适应算法。为了解决这个问题,研究者们提出了两种解决思路,一是仍然使用基于二阶统计量的代价函数构成算法,但是引入一些简化手段来量化计算中的误差,如符号算法。在自适应滤波算法中,滤波器系数的调整通过误差的反馈来实现。经过量化后,可以很大程度简化计算误差,从而在一定程度上减少来自于非高斯噪声的干扰。此类算法可以基于LMS算法,也可以基于APA算法,如文献[5]中提出的仿射投影符号算法(APSA)。但是,这一类算法不能从根本上解决问题,因为符号算法只是在计算误差上做了简化运算,没有从根本上解决非高斯噪声对二阶统计量的破坏问题。基于这种符号运算的算法可能会因为符号运算的引入,使整个算法收敛速度慢甚至发散。针对此,研究者们提出了一系列基于非二阶统计量的代价函数,如基于最大相关熵准则(MCC)[6]代价函数的成比例归一化最大相关熵准则算法(PNMCC)[7]和基于最小误差熵(MEE)[8]代价函数的成比例最小误差熵算法(PMEE)[9]。研究者们利用熵这种具有局部相似性的函数替代传统的二阶统计量,建立了一个新的数学模型,然后利用熵这种不确定性的度量来更好地描述非高斯噪声,从而在根本上解决非高斯噪声对算法的严重干扰。只有很好地解决稀疏系统和非高斯噪声的问题,自适应滤波算法才能保证那些在特定环境下的工程应用更好地工作。
1 传统算法的分析
1.1 Alpha稳定分布噪声
非高斯噪声有很多种类,本文采用其中一种常见的Alpha稳定分布噪声进行分析。对于一个随机变量X,如果它的特征函数Φ满足[10]:
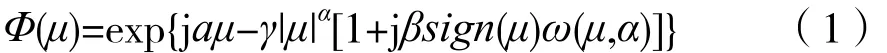
就称此随机变量X服从稳定分布。
由式(1)可知,Alpha稳定分布方程中,涉及到α、β、γ、α四个参数。稳定分布的特性也由这四个参数决定,其中α称为特征指数,决定了稳定分布的概率密度函数图像拖尾的厚重程度,取值在0~2。当α=1时,稳定分布服从柯西分布。α=2时,稳定分布服从高斯分布。α的取值越小,稳定分布的冲击性越强,反之亦然。β被称为对称参数,表示稳定分布的概率密度函数偏离分布中心的程度。当β=0时,此时稳定分布也被称为对称稳定分布,其概率密度函数的图像关于中心左右对称。γ被称作分散系数,表示稳定分布中的各点对于分布中心的离散程度。a是分布中的位置参数,代表分布的概率密度函数的中心位置。本文中主要考量稳定分布冲击性的参数是α,可以粗略认α的值被设置的越大,所得到的噪声的冲击性就越强。图1给出了在α取不同值时的稳定分布概率密度曲线。从图1可知,这种Alpha稳定分布非常适合来描述概率密度曲线类似于高斯分布,但同时有着很强的冲击性的非高斯分布。在非高斯噪声的环境下,稳定分布是不存在二阶矩的,即该随机变量不存在方差这一参数。所以,这种非高斯噪声严重破坏了基于二阶统计量作为准则的自适应滤波算法。
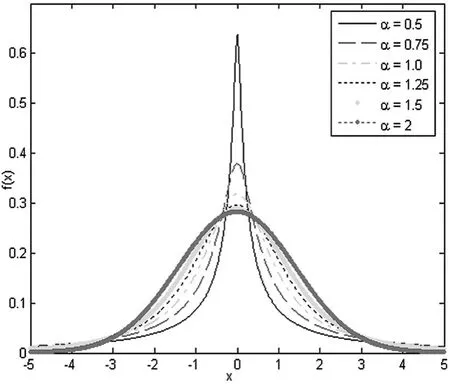
图1 当特征指数α取不同值时稳定分布的概率密度曲线
因为对特征指数α进行调整可以直接改变其概率密度函数的波形,所以可以通过调整α来模拟不同冲击程度的非高斯噪声。
1.2 基于系数比例步长分配的自适应滤波算法
本文采用存在于稀疏信道中的回声消除系统作为例子来说明算法的有效性。回声消除系统作为一种在语音通信中消除回声的手段,可以很好地抵消信号回声对通信造成的严重影响。回声消除系统本质上是系统识别的一种,通过采用某一种自适应滤波算法,依靠每次迭代后得到的计算误差e(k),驱使自适应滤波算法进行下一次更新。通过计算误差e(k)的监督,使得模拟的未知系统从初始值慢慢向实际的未知系统的真实值靠近,直到最后达到或者无限趋近于真实值,从而使人为设置的初始系统模拟出未知系统的全貌。这种系统识别方法的原理如图2所示。
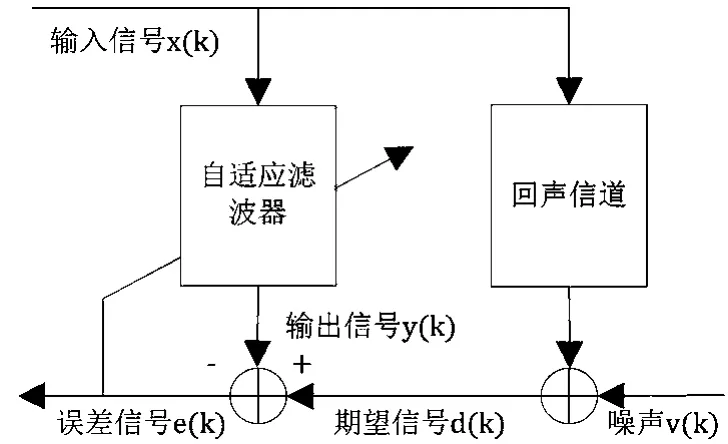
图2 基于自适应滤波算法的噪声抵消系统
文献[2]中,提出了一种可以重新分配各滤波器抽头系数的算法步长的归一化最小均方算法(NLMS),即PNLMS。这种算法对于解决在稀疏信道中算法均分步长造成的浪费所导致的不稳定问题提出了一种很好的思路。更新方程为:

其中,滤波器的抽头系数为:
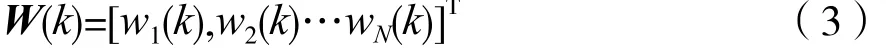
整体思路基于最小均方算法,核心在于引入比例系数矩阵G(k),是以gn(k)作为其主对角线元素的对角矩阵,定义为:
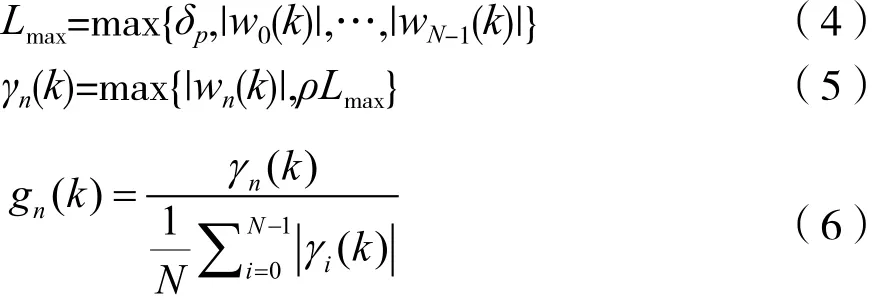
Benesty在文献[11]中提出了一种系数比例方法的改进算法,即改进的成比例归一化最小误差算法(IPNLMS)。算法中最主要的改进在于比例系数的步长参数gn(k),其定义为:
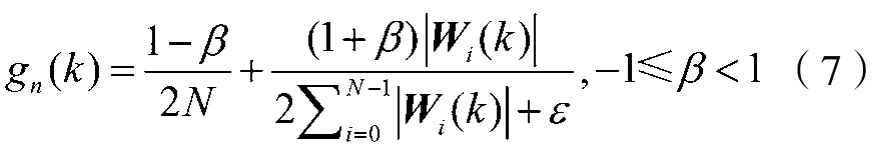
这种算法有着更合理的步长分配机制,同时又有着不慢于PNLMS算法的收敛速度。在处理非稀疏问题时,这种算法依然可以保持着不慢于最基础的归一化最小均方算法(NLMS)的收敛速度。此算法通过对参数的调整,使得算法本身介于NLMS算法和PNLMS算法之间,同时拥有对信道稀疏度的适应性和对非稀疏系统的稳定性两种优点。
引入成比例思想后,针对稀疏系统的自适应滤波算法的范围迅速扩展。基于支持算法的硬件的快速发展,对算法的收敛速度的需求开始大于对算法复杂度的要求。一种收敛速度快的算法往往可以被广泛应用,所以数据重用技术被引入自适应滤波算法,基于这种方法的算法也被称为仿射投影算法(APA)。仿射投影算法的更新方程与归一化最小均方算法一致,区别在于输入信号将X在数据重用后记为Xap,其中P为投影阶数。
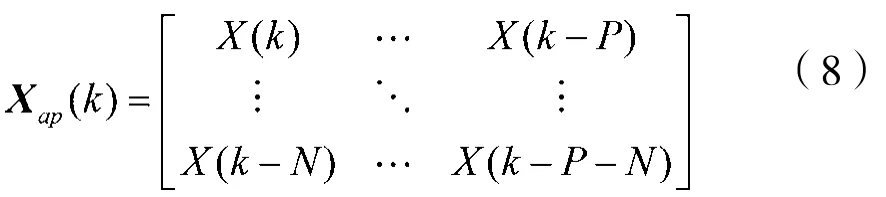
基于此,所有以NLMS为基础的算法都可以经过输入信号的数据重用后变为仿射投影(AP)类的算法,如PAPA[12]的更新方程为:
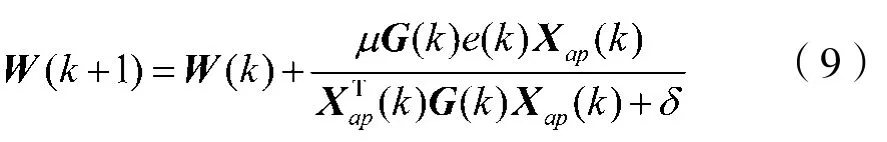
其中的比例矩阵G(k)的主对角线元素gn(k)按照式(4)、式(5)和式(6)更新。
按照这种思路,文献[13]提出了改进的成比例仿射投影算法(IPAPA)。它与PAPA算法的主要区别为比例矩阵G(k)的主对角线元素gn(k)按照式(7)更新。在以上这些成比例算法的基础上,Deng等人进一步对比例矩阵的模型进行优化,提出了μ律成比例归一化最小均方算法(MPNLMS)[14-16]和简化的成比例归一化最小均方算法(SPNLMS)[14-16]。至此,这两种算法的出现,基本解决了在稀疏信道中算法步长合理分配的问题。
1.3 基于符号运算的自适应滤波算法
在解决非高斯噪声的问题上,研究者首先通过某种特殊的运算达到简化计算误差e(k)的目的。符号函数是一种有着量化作用的函数,其定义为:
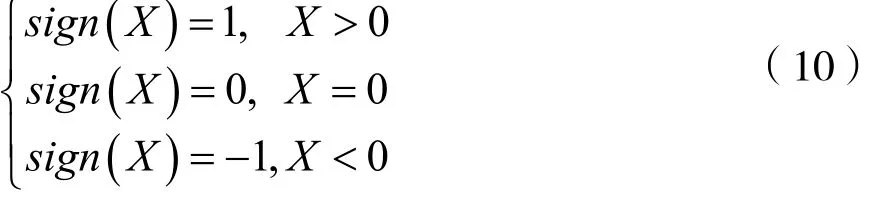
通过符号函数sign(X)量化误差e(k),从而使误差从无数种可能性简化为三个固定的取值。这样算法本身只能通过三种固定的误差值进行更新迭代,使得算法更加不易受到外界有着冲击性的噪声干扰,从而在某种程度上回避了非高斯噪声的破坏性影响。代表算法有仿射投影符号算法(APSA),其更新方程为:

一定程度上通过符号运算解决了非高斯噪声的影响后,人们在考虑是否可以同时解决经常并行存在的非高斯噪声和稀疏系统的问题。所以将比例系数的思想和符号运算同时引入APA算法,就可以得到新的成比例的仿射投影符号算法(PAPSA)和(IPAPSA)。其更新方程为:
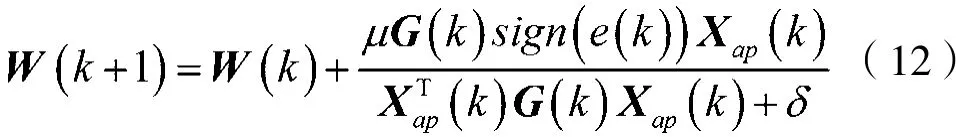
其比例矩阵G(k)的主对角线元素gn(k)按照式(7)更新。
至此,自适应滤波算法可以在一定程度上抵御在稀疏系统中非高斯噪声的影响,这些算法在如水下噪声消除、房间中的通话回声抵消等系统中得到了很好的应用。
2 基于非二阶统计量的新算法
2.1 基于最大相关熵的自适应滤波算法
对于随机变量X,它的Shannon熵被定义为:

其中N表示数据的个数,Pk表示第k个数据出现的概率。Renyi在Shannon熵的基础上,进一步提出了α阶Renyi熵,其表达形式为:
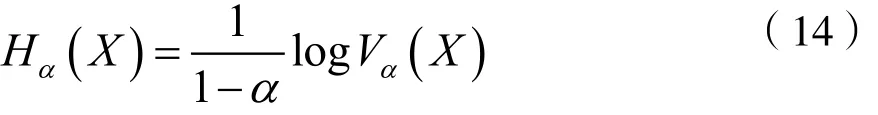
其中Vα(X)被称为α阶信息势能,本文中使用的是当α=2时的二阶信息势能。它通过Parzen窗法得到的估计值为:

其中Kσ2为核函数,σ为核函数的长度。常见的核函数有多项式核函数和高斯核函数。出于对核函数的泛用性考量,文中选用的为高斯核函数,其表达式为:

将式(16)代入式(15),可得到关于随机变量X与Y之间的互相关熵的表达式:
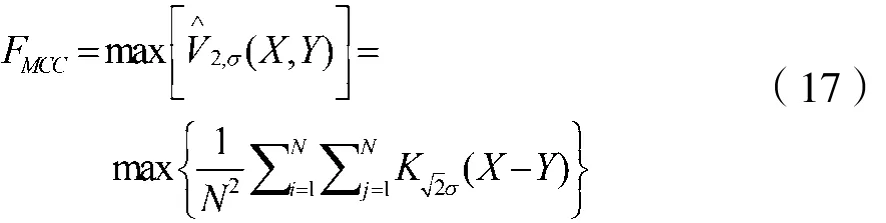
基于此,Liu提出了一种基于最大相关熵准则(MCC)的仿射投影算法(MCCAPA)[17],其更新方程为:
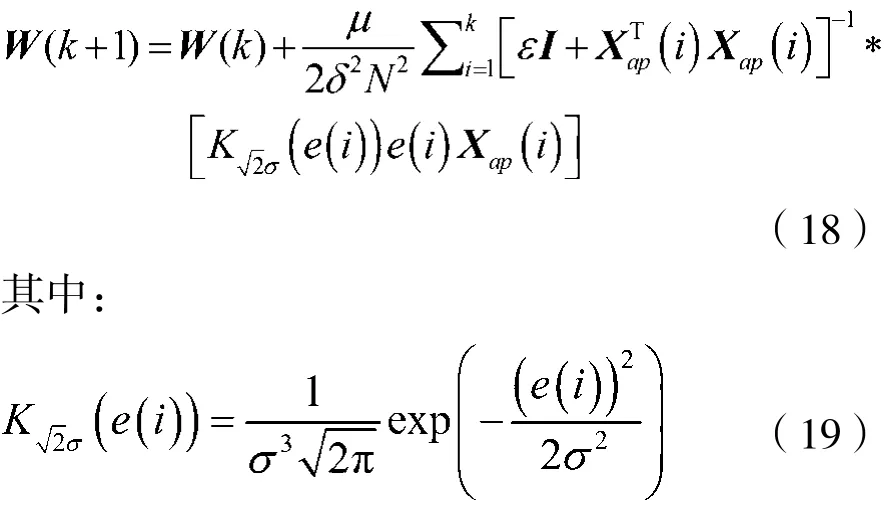
至此,MCC准则的引入,使得自适应滤波算法从真正意义上摆脱了二阶统计量的束缚,大幅增加了对于非高斯冲击噪声的抗干扰能力。
2.2 基于最小误差熵的自适应滤波算法
利用熵这种对于不确定性的度量,研究者们又提出了一种同样基于Renyi熵,但是约束对象从输入信号变为计算误差的新理论,即最小误差熵理论(MEE)。Peng在这种理论的基础上提出了一种成比例的最小误差熵算法(PMEE)[9]。由式(17)可知,当相关熵的输入部分变为两次计算的误差之间的差值时,相关熵就变为了误差熵(Error Entropy)。误差熵的原理是使两次计算误差之间的差值的混乱程度最小,使得计算误差e(k)逐渐随着迭代次数趋向规律。这样就可以通过一个量来约束误差的混乱程度,从而使每次迭代后进入自适应滤波器的误差反馈可以更加规律地反映每次计算的效果,保证计算误差平稳减小,直到最后无限趋近于零。基于最小误差熵理论的代价函数为:
将MEE的代价函数对滤波器抽头系数W求偏导并代入梯度下降法[18]的框架:

可以得到新的PMEE算法的更新方程为:

其中比例系数矩阵G(k)的主对角线元素gn(k)按照式(4)、式(5)和式(6)更新。PMEE是一种在抵御非高斯噪声干扰时,同时兼顾稀疏系统的算法。
在此基础上,可以引申出更加复杂的算法,进一步加强自适应算法在特定环境中的适应性。例如,可以将改进的比例系数矩阵(7)引入PMEE算法,或者将μ律的成比例矩阵(MP)、简化的成比例矩阵(SP)引入其中,得到IPMEE算法、MPMEE算法或者SPMEE算法,使得算法在二次分配步长时同样能保证较快的收敛速度和较低的计算复杂度。
3 实验结果
3.1 实验中的参数设置
将各类算法应用至图2所示的自适应回声抵消系统中,本文使用MATLAB进行仿真。实验中采用由式(23)生成的稀疏信道对稀疏系统进行模拟。
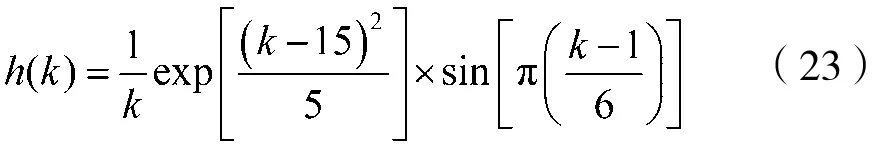
本文中通过使用二阶AR模型(24)将高斯白噪声有色化来模拟语音信号,其表达式为:
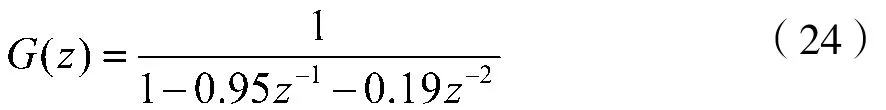
实验中设置的未知信道的阶数和滤波器阶数均为120阶,迭代次数为40 000次。涉及到仿射投影的算法,其投影阶数均为P=4,信噪比SNR=10。非高斯噪声由Alpha稳定分布生成,其分布中的特征指数α=1.2。噪声的图像如图3所示。
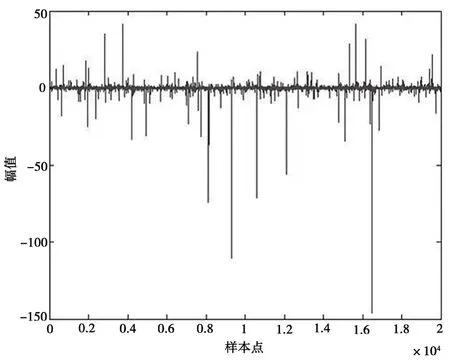
图3 当α=1.2时由稳定分布所生成的非高斯噪声
使用归一化均方偏差(NMSD)作为衡量算法性能的指标,其定义为:

其中wi为每次迭代后的滤波器抽头系数,w0为未知信道的真实值。通过NMSD可以整体上表述经过自适应算法调整过后的初始滤波器抽头系数与未知信道之间的偏离。这个值越小,说明算法调整后的自适应滤波器越逼近未知信道。NMSD值下降的越快,说明算法的收敛速度越快。而NMSD值进入平稳状态后波动越小,说明算法对未知信道的跟踪能力越强。
3.2 仿真结果及分析
本文选用了PMEE、MCCAPA、PAPA、PAPSA以及IPAPSA五种算法进行对比,其中囊括了基于二阶统计量(PAPA,PAPSA,IPAPSA)和非二阶统计量(PMEE,MCCAPA)的算法,分别包含两种不同的比例矩阵的算法(P/IP),以及基于传统的LMS类(PMEE)和基于数据重用的APA类(MCCAPA,PAPA,PAPSA,IPAPSA)算法。仿真得到的各算法NMSD曲线如图4所示。
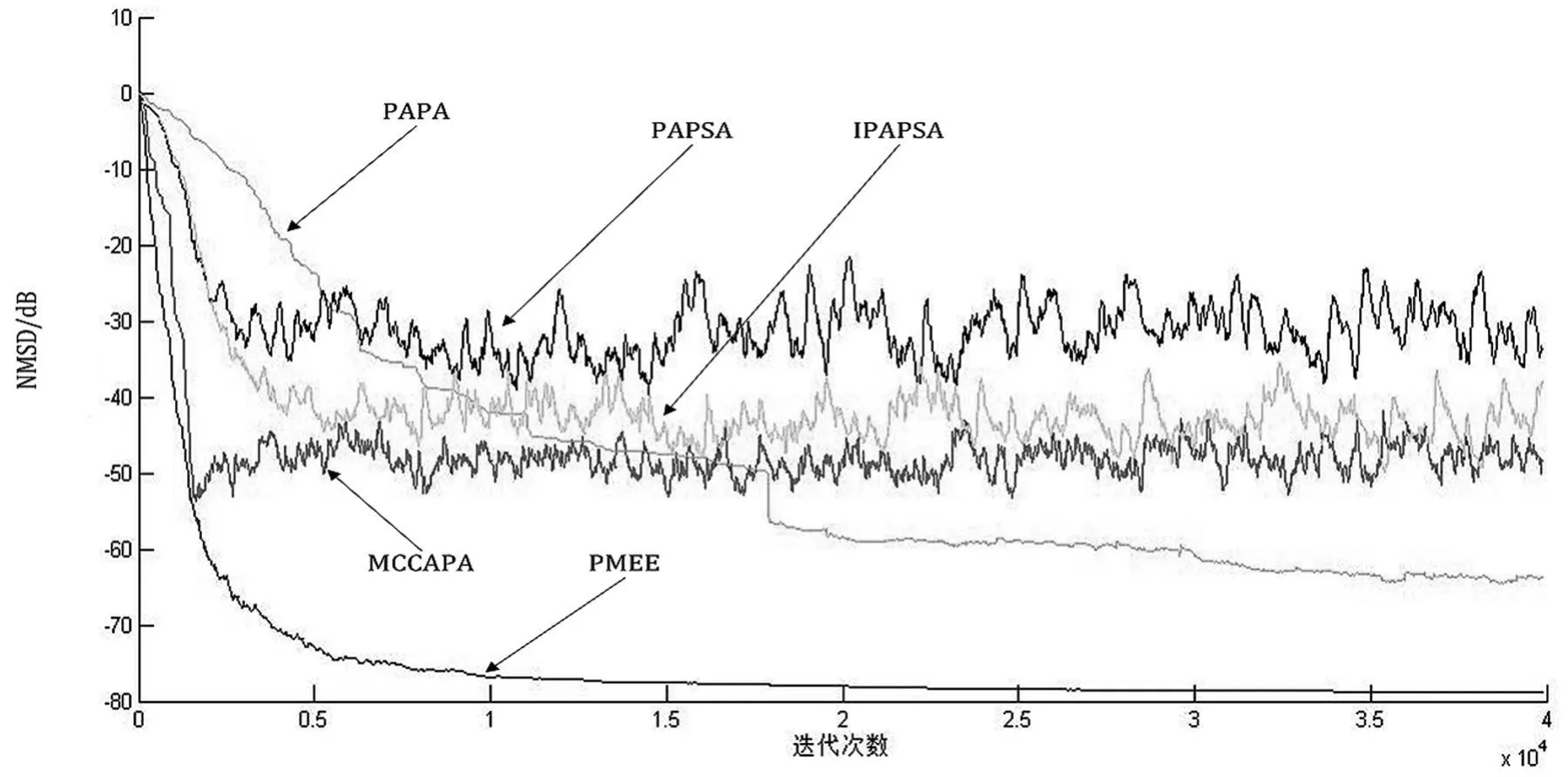
图4 文中各类算法的NMSD曲线
通过实验可以明显观察到,同时兼顾稀疏系统特性和非高斯噪声干扰的PMEE算法有着最快的收敛速度、最低的NMSD值和波动最小的平稳状态。此外,和PMEE收敛速度类似,但是波动稍大的是MCCAPA算法,但是这种算法的NMSD值却相较于PMEE算法大很多。可见,在稀疏信道中,稀疏性的干扰会对没有采用比例系数方法的算法造成较大程度的破坏。对于PAPSA和IPAPSA两种算法,由于采用的都是APA的算法基础,所以它们有着类似的收敛速度。但是,由于改进后的比例系数矩阵可以更加合理地分配步长,因此基于IP的算法IPAPSA在稀疏系统中有着比PAPSA算法更加低的NMSD值。以上四种方法从整体上比较,基于非二阶统计量的两种算法(MCCAPA,PMEE)要优于基于传统二阶统计量并使用符号运算进行误差量化的两种算法(PAPSA,IPAPSA),改进后的成比例算法(IPAPSA)要优于传统的成比例算法(PAPSA)。在以上选择的五种算法中,表现最差的为成比例仿射投影算法(PAPA)。因为它既没有采用改进后的比例系数矩阵(IP),也没有采取任何抵御非高斯噪声的手段,所以在这两种负面环境的强烈干扰下,此算法基本失效。
4 结 语
本文针对稀疏系统和非高斯噪声两种对自适应滤波算法有着严重影响的环境进行了分析,并且选用了五种现有的算法进行仿真比较。经过仿真验证后发现,在稀疏系统中,比例系数矩阵可以保证算法分配出较大的步长给不为零的信道点。对于值为零或者趋近于零的信道点,则分配以较小的步长,在此基础上建立的更加合理的分配方法即为改进的比例系数矩阵。基于这种方法的算法在稀疏系统中比起基于未改进的传统比例系数矩阵的算法有着较低的稳态值。未在本文中列举的新的成比例算法,如有着更快收敛速度的μ率成比例方法(MP)、有着和MP方法几乎同样的收敛速度、计算复杂度较低的简化成比例方法(SP)。如果将它们应用于对非高斯噪声有鲁棒性的算法中,可以起到更好的效果。
对于非高斯噪声的影响,目前主流的解决方法分为两大类,即采用量化误差的手段和使用非二阶统计量重新构造代价函数的手段。本文在实验中也选用了属于这两大类中的五种算法,分别验证了二者的优劣。经试验验证,非二阶统计量(例如Renyi熵)能够更加准确地描述非高斯噪声。这种代价函数要比传统的代价函数更加适用于非高斯噪声中的鲁棒性算法的构造。无论是最大相关熵算法(本文中选用的算法为MCCAPA)还是最小误差熵算法(本文中选用的算法为PMEE),其在非高斯噪声中的表现均要好于其他种类的算法。
由于稀疏系统和非高斯噪声广泛存在于自然界,未来自适应滤波算法和其自适应的设计思路也会被应用于更加广泛的领域。这样不免会出现以上两种情况同时存在对自适应算法的干扰。针对这种情况,系数成比例思想和非二阶统计量将成为两个重要的解决问题的工具,并被广泛应用于如稀疏信道估计、水下噪声消除等领域。虽然这两种方法都存在一定的不足,如非二阶统计量会增大算法的计算复杂度,增加硬件设备的计算量,但其对自适应滤波算法已经产生了深远影响。今后研究者们也会进一步加强对稀疏系统和非高斯噪声问题的研究,提出收敛速度更快、稳定性更高、对未知系统跟踪效果更好的自适应滤波算法。
