基于随机网络演算的CBTC车-地无线通信时延分析

韩江磊,陈永刚

(兰州交通大学自动化与电气工程学院,兰州 730070)

LTE(Long Time Evolution，长期演进)技术作为目前移动无线技术最高级别的演进方向，其性能已然超过了WiFi和WLAN技术，完全可以匹配CBTC系统(Communication Based Train Control System，基于通信的列车自动控制系统)车-地无线通信的需求[1]。郑州地铁1号线、朔黄铁路、重庆轨道交通5号线等运用LTE技术的成功案例也证实了TD-LTE的可行性，因此，基于LTE的城市轨道交通车地通信系统(LTE-M)是大势所趋[2]。LTE系统因为其较高的频谱利用率，完善的多业务优先级调度机制，能实现单系统对多业务的综合承载等特点而完全匹配地铁车地无线业务需求[3]。LTE为保障城市轨道交通安全运营提供技术支撑，形成我国在城市轨道交通通信技术和装备方面的优势。综上所述，CBTC信号系统的车地无线通信系统采用LTE技术，是目前地铁通信的最佳选择。

基于LTE的城市轨道交通车地通信系统(LTE-M)在高速环境中也面临着巨大的挑战，比如列车无线承载业务严格的QoS(Quality of Service，服务质量)要求等。一方面为了列车能够安全可靠运行，另一方面为了能够合理优化车地无线通信网络的有限资源，必须对车地无线通信系统进行准确的性能评估及预测[4]。目前，人们更多研究的是在低速环境下网络性能的分析，而在高速环境下，由于更严重的多径效应和多普勒频移，其网络性能的研究相对较少。以往对城际铁路和高速铁路无线通信网络性能分析大多都使用各种仿真手段，比如基于半实物的仿真平台、无线移动模拟器平台[5-7]等，这些方法虽然可以准确进行分析网络性能，但是却需要消耗大量的时间和经济成本，这不利于实际应用。随机网络演算作为一种较为先进的能够进行网络性能分析的重要理论算法，它是确定性网络演算理论的概率版本，二者都属于网络演算的范畴。通过确定性网络演算只能得到系统最差情况下的性能边界，而对于时变系统来说，网络性能达到最差性能的概率非常小，如果按照系统最差性能的情况配置网络资源势，势必会造成资源浪费；随机网络演算准许系统以一定的违约概率来超过性能边界，从而得到网络性能的统计边界，在得到系统的服务质量保障之后进一步获得更高的资源利用率和统计复用增益[8-11]。本文通过随机网络演算理论，对地铁无线承载业务中的CBTC业务进行分析并建立相关的数学模型，并通过理论推导得到车地通信的时延边界，最后采用MATLAB仿真工具对理论边界进行分析。

1 随机网络演算

随机网络演算经过多年的发展逐渐演变为以Jiang为代表的基于互补累积分布函数(Complementary Cumulative Distribution Function，CCDF)的随机网络演算[12]和以Fidler为代表的基于矩母函数(Moment Generating Function，MGF)的随机网络演算[13]。无论是基于CCDF的随机网络演算还是基于MGF的随机网络演算，其核心理论基础都是最小加代数，并通过最小加代数理论推导出业务的到达曲线和信道服务曲线，从而进一步得到网络性能边界曲线。基于互补累积分布函数(CCDF)的随机网络演算公式较多、运算量大并且复杂度高，这极易导致在公式推导和参数优化的过程中出错，而基于矩母函数(MGF)的随机网络演算，利用有效带宽和矩母函数的转换关系，巧妙地简化了很多纷繁复杂公式推导过程而又不影响最后结果的准确性[14-15]。所以所选择的算法为基于矩母函数(MGF)的随机网络演算。

1.1 基于MGF随机网络演算的数学基础

定义1(矩母函数) 对于随机过程X(s，t)，其数学期望为eθX，则有随机过程X(s，t)的矩母函数MX(θ)为

(1)

矩母函数是基于矩母函数(MGF)随机网络演算的重要数学基础，可以通过有效带宽理论，根据业务流到达过程和服务过程的有效带宽，来推导出其相应的矩母函数，而矩母函数很好地描述了随机变量的概率分布，直观地刻画了系统的到达过程和服务过程。

定义2(有效带宽) 有效带宽是指当信源为时变信源时，业务的服务质量能够保证并且网络资源能够被充分利用的前提下，系统能够提供的最小带宽，以满足服务质量的要求。

有效带宽δX(θ，n)与矩母函数MX(θ，n)存在如下的转换关系

(2)

1.2 基于MGF随机网络演算的分析过程

由于在基于矩母函数(MGF)的随机网络演算中，对于一个随机过程X(n)，其矩母函数为：MX(θ，n)=E[eθX(n)]，所以业务流的到达过程A(n)和服务过程S(n)相对应的随机到达曲线和随机服务曲线的MGF函数分别为

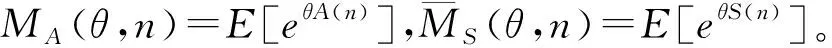
D(n)=inf{d≥0:A(n)≤A*(n+d)}

(3)

式中，A*(n)表示数据流的离开过程，又根据Lindley递归理论可得如下公式

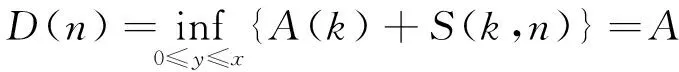
⊗S(n)

(4)

通过对公式(3)、公式(4)进一步分析，可推导出系统时延满足如下关系

P{D(n)>x}≤P{A(n)>A*(n+x)}≤

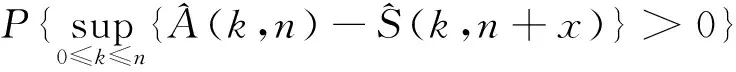
(5)

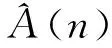
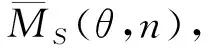
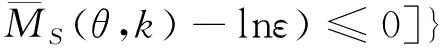
(6)

2 系统模型

2.1 CBTC列控信息承载业务的通信时延

在基于LTE技术的车-地无线通信综合承载的业务中，从列车安全运行的角度考虑，CBTC实时数据传输业务优先级最高。只有CBTC无线传输使列车和地面之间进行实时可靠的双向交换，才能保证列车安全高效的运行。CBTC列控业务要求当列车运行速度最高达200 km/h时，通信系统单路单向传输时延不超过150 ms的概率不小于98%，这里包含了有线传输和无线传输，而无线网络的延迟应满足小于100 ms的要求。

2.2 系统业务到达模型

要建立准确的业务模型，首先要根据业务特征及自身属性来对其进行准确的分析。通常CBTC列控系统以200 ms的通信周期进行车地双向通信。前行列车通过上行链路将自身的列车状态信息发送给区域控制器(ZC)，ZC接收到信息后计算出行车许可(MA)，并通过下行链路将MA发送给后方列车。如图1所示，在第j个周期，列车j在向区域控制器ZC发送列车状态信息时发生了上行时延；在第j+1个周期，区域控制器ZC在向列车k发送行车许可MA时发生了下行时延。对于上行时延，区域控制器ZC会将前行列车的状态信息进行估计并将结果发送给后方列车；而对于下行时延，列车会以上一周期前行列车的状态信息和区域控制器ZC发送的行车许可MA作为控车信息。

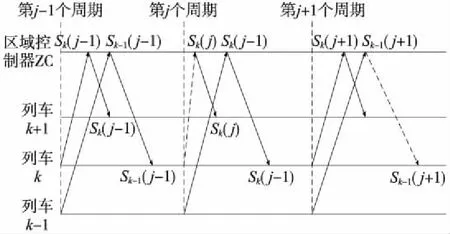
图1 车地通信时延示意

综上所述，CBTC列控业务是一个周期性的业务流，因此可以将业务到达模型建立为周期性信源模型。假设此周期性信源模型的业务流A(n)的信源在时刻{n=Uτ+cτ，c=0，1，2，3，…}能够产生σ的业务量，其中，U是初始时刻并且满足在[0，1]之间的稳态分布。则对于n≥0和θ≥0，数据流A(n)的有效带宽为

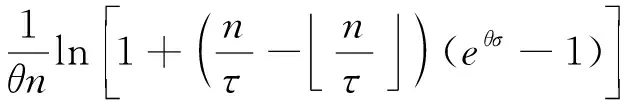
(7)

而又根据式(2)可以推导出A(n)的矩母函数为

(8)

2.3 系统信道服务模型

近年来，有限状态马尔可夫信道(Finite-state Markov channel，FSMC)模型作为重要的分组级信道模型而得到了广泛的研究。通常情况下，一般的一阶FSMC模型在慢衰落或中等速率衰落信道中比在快衰落信道中更为精确、适当。在高速移动的场景中，快速衰落(小尺度衰落)、阴影衰落(大尺度衰落)和路径损耗会因为快速移动而产生迅速的变化；另外，LoS路径存在于典型的多路径环境中，当列车沿着铁路行驶时，平均接收信噪比(Signal Noise Ratio，SNR)会产生周期性的波动。所以在列车高速移动的场景中，传统的FSMC模型已不再适用。本文使用一种基于快速移动场景下列车无线通信信道的多维度FSMC模型[16]。如图2所示，它将相邻两个eNodeB(LTE基站)的区域划分为若干个区间，在每个区间中，把快衰落信道和阴影衰落信道分别建模为Rician信道和Lognorma信道，并且传播模型是基于WINNER II模型中的D2a子场景模型[17]。

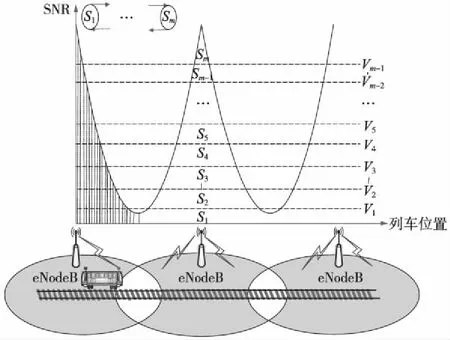
图2 车-地无线通信衰落信道

由于LTE-M采用专有频段，所以就避免了公共信号的干扰；另外，LTE-M采用了干扰抑制合并(IRC)、波束赋形(BF)和小区间协调干扰(ICIC)技术，有效地避免了同频干扰并抑制了系统内部的相邻小区干扰；又因为相邻小区的平均干扰功率远远小于接收端的平均功率，所以本文暂时不考虑相邻小区的干扰。首先，通过使用接收到的SNR来确定信道的状态。把接收到的SNR范围划分为m个区间(区间不重叠)，例如，[0，v1)，[v1，v2)，…，[vm-1，∞)，其对应于S1，S2，…，Sm，并用r1，r2，…，rm来表示相应信道状态的信道传输速率，其中vk为SNR阈值，Sk为第k个信道状态，rk为Sk的传输速率，k∈{1，2，3，…，m}。这其中采用自适应调制和编码(AMC)技术来最大限度地增大系统容量和带宽效率，AMC技术可以根据不同的状态来调整传输速率。

假设两个相邻LTE基站之间有I个区间，在区间i(i=1，2，…，I)中，Sk的稳态概率分布可以通过对整个区域的SNR的概率密度函数fΓi进行积分而获得

(9)

其中，FΓi(vk)为区间i的SNR的累积分布函数。

状态转移概率可以通过电平通过率(Level Cross Rate，LCR)Λ(vk)来近似计算，LCR是分析信道衰落的二阶统计量，其描述了信道衰落的频率。正如上文所提，列车车地通信信道是伴有LoS路径的莱斯衰落信道，所以莱斯衰落信道的LCR为[18]

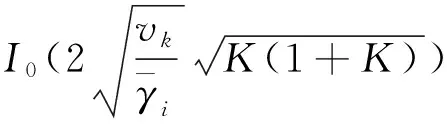
(10)

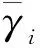
(11)

其中，ht为一个时隙内接收信号功率快衰落的增益。

莱斯衰落信道模型选择Nakagami-m信道模型，其瞬时接收SNRγi的概率分布函数为

(12)

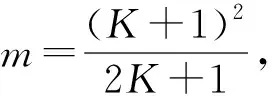
由此可以将状态转移概率表示为

(13)

进而可以表示出稳态概率分布向量πi和区间i(i=1，2，…，I)的状态转移矩阵Qi为

最后，可以推导出区间i的信道服务过程的MGF函数为

(14)

式中，R(θ)为传输速率rk的对角矩阵diag(eθr1，eθr2，…，eθrm)；lm为单位列向量。

将式(8)、式(14)中的到达过程与服务过程的MGF函数代入式(6)中，即可得到时延边界的表达式。

3 理论与仿真结果分析

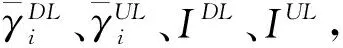
表1是系统仿真的主要参数。其中基站发射功率和车载终端功率都是最大值。由于研究的对象是CBTC业务，而地上单网在5M频段下只能优先保证CBTC业务，所以带宽选为5 MHz。假设两个eNodeB之间的间距为2 km，并且每个区间的长度为5 m，则相邻两基站中间有400个区间。经简单计算可知，列车在每个区间i停留的时间大约为150 ms，只要求出列车的瞬时传输速率，即可求解出列车在这150 ms周期内通过莱斯衰落信道的数据量，继而根据以上理论分析算出时延性能。采用自适应调制和编码(AMC)技术，而AMC技术可根据信道状态来调整传输速率。通过式(11)、式(12)得到瞬时SNRγi所对应的区间i，然后根据已知的调制编码方案(Modulation and Coding Scheme，MCS)索引找到区间i相对应的瞬时传输速率，如表2所示，根据合适的SNR范围得到6个MCS及其参数。仿真次数则根据区间i的数量决定，即仿真i次，每次仿真106个时间单位。由于上行方向和下行方向的延时边界性能分析所用到的理论一样，而又因为在列控系统中，下行方向的业务量大于上行方向，所以只分析下行方向。

表1 系统仿真参数

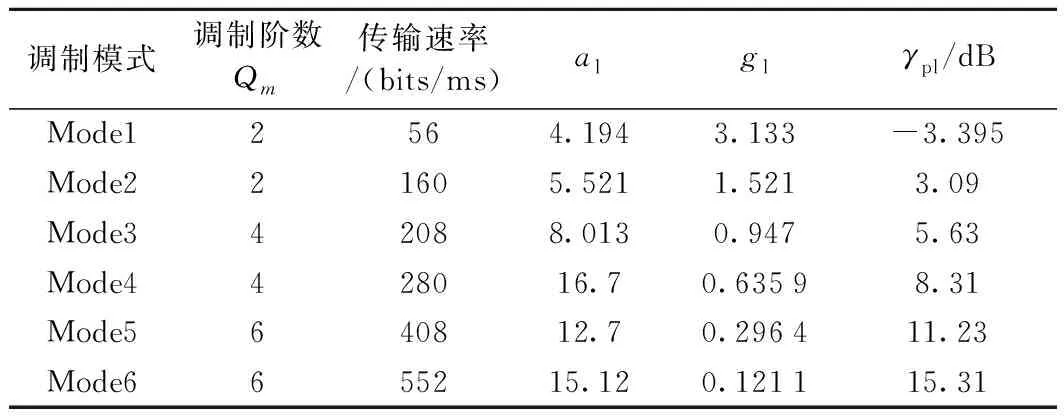
表2 平均SNR与对应的瞬时传输速率

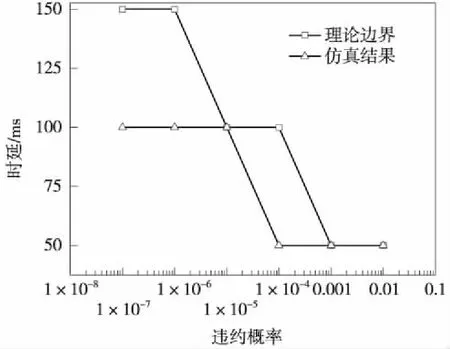
图3 不同违约概率下仿真与理论结果对比

如图3所示，将业务模型的数据包σ和周期τ分别设置为：σ=4 000 bits，τ=6 s。当违约概率为{1×10-7，1×10-6，1×10-5，1×10-4，1×10-3，1×10-2}时，时延会随着违约概率的增大而减小，当违约概率极限接近0时，则此时的延时边界称为保守边界，即网络性能边界的“最坏情况”。在实际应用中，可以根据不同业务在不同时延的违约概率，对网络资源进行合理分配，可以有效避免资源浪费。

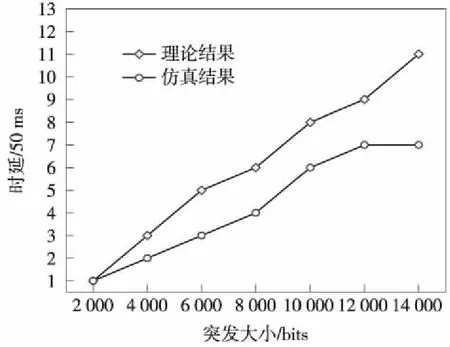
图4 不同突发大小下理论与仿真结果对比

如图4所示，业务流的到达周期为τ=120个时间单位(6 s)，数据包大小为{2 000，4 000，6 000，8 000，1 000，12 000，14 000}bits。以违约概率1×10-7为例，时延随着突发大小的增加而增加，即数据包越大，则时延越大。另外，由于业务流的到达周期始终大于数据包在传输过程中的时延，所以在突发大小2 000～14 000 bits，数据包是可以被完全传输的。

选取以列车所在小区基站开始的前50个区间，违约概率为1E-2，数据突发大小为σ=4 000 bits，业务流的到达周期为τ=6 s。由图5可知，时延随着区间数量的增加而不断增大，显而易见，这是由于列车在移动的过程中与eNodeB之间的距离增加造成的。

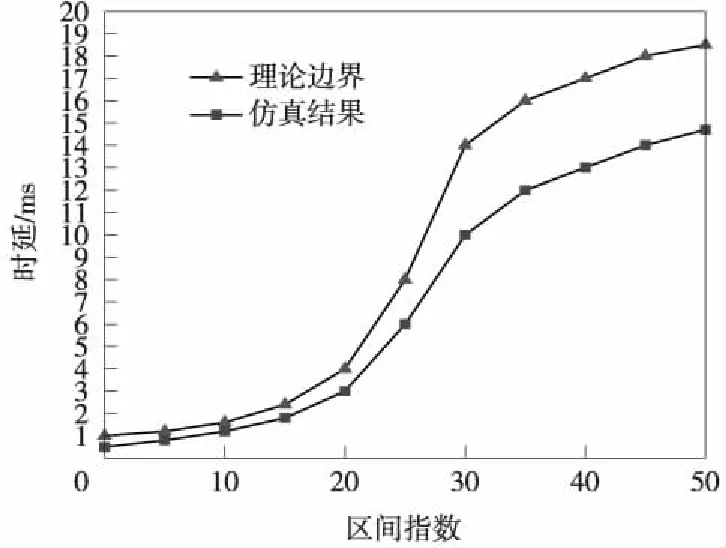
图5 不同区间指数下理论与仿真结果对比

4 结论

本文主要研究了基于矩母函数(MGF)的随机网络演算在CBTC车-地无线通信时延分析中的应用。首先，根据CBTC无线通信的自身特点建立有效的业务模型和信道模型，而后基于MGF的随机网络演算步骤求解出到达曲线和服务曲线，然后推导出延时边界，最后运用MATLAB仿真软件对理论分析结果进行对比验证。从微观角度看，虽然最后得到的理论结果并不能完全吻合仿真结果，但是其误差相对较小；从宏观角度看，基于MGF的随机网络演算的理论分析，很好地描述了在不同约束条件下的时延规律和特性，对研究CBTC综合承载的其他无线通信业务以及性能指标具有重要的参考价值。