立交桥匝道放样方案设计

马义超，米鸿燕，钟 凯



立交桥匝道放样方案设计

马义超，米鸿燕，钟 凯

（昆明理工大学国土资源工程学院，云南 昆明 650093）

本文通过对立交桥测量方案设计的研究，并以互通式立交桥为例得出在立交工程施工时，测量人员需要做的工作以及对各项测量工作的安排。最后，通过对立交匝道中边桩坐标计算软件的设计与应用，并对测量放样数据进行了相关计算与检核。

互通式立交桥；坐标计算；放样数据；检核

0 引言

立体交叉主要由跨线构造物、正线、匝道、出入口、变速车道与集散车道等几部分组成[1]。（1）跨线构造物。主要指从主体结构上方或下方穿过的构造物。（2）正线。立体交叉的主体结构，交通量较大，包括主线和次线。（3）匝道。是主线车辆实现转弯的重要结构组成。（4）出入口。供车辆由正线进入或驶出。（5）变速车道。可分为加速车道和减速车道，在正线出入口附近设置。（6）集散车道。与正线平行但分离开来的车道。除以上主要组成部分之外，立体交叉还包括立交范围内的绿化地带、管线设施以及照明通信设施[2]。

1 立交原理与分析

1.1 立体交叉的设置条件

立体交叉作为一项大型工程，其设置条件也需经过多方面的考虑，不仅要从交通方面，还要对经济条件以及可持续发展性做相应的考虑[3]。如我国一些城市或高速路口修建立体交叉时，没有从长远方向考虑，建成之后非但没有改善交通，还造成了更为严重的交通拥堵，所以立体交叉的设置条件也十分重要[4-5]。立体交叉设置的条件需考虑以下方面，如图1所示。

1.2 匝道施工测量

在进行匝道施工前，应先核对匝道与正线以及匝道与匝道交接位置的数据，包括各点的里程、平面坐标、高程以及横纵断面数据，若检核发现有数据冲突，应上报项目工程部。

施工测量时，首先测设出道路中线以及边线，以供路基施工，在中心线桩上需标出设计高程与基层的松铺厚度[6]。路基施工完成以后，进行道路基层的测量放样，每隔五米测设一个点位，要求有平面坐标与高程，并将桩定设在路线外五十公分处，考虑其松浦系数，压实之后应及时复核桩位高程，为后续施工工序提供依据。基层施工完成以后，需要放出路缘石内线位置，待路缘石施工完成后，在路缘石侧面需测设路面高程控制点，便于后续路面施工的控制测量[7]。每道工序都需要认真检核，检核无误之后，向监理工程师报检复核通过以后，才能开始下一道工序[8-9]。

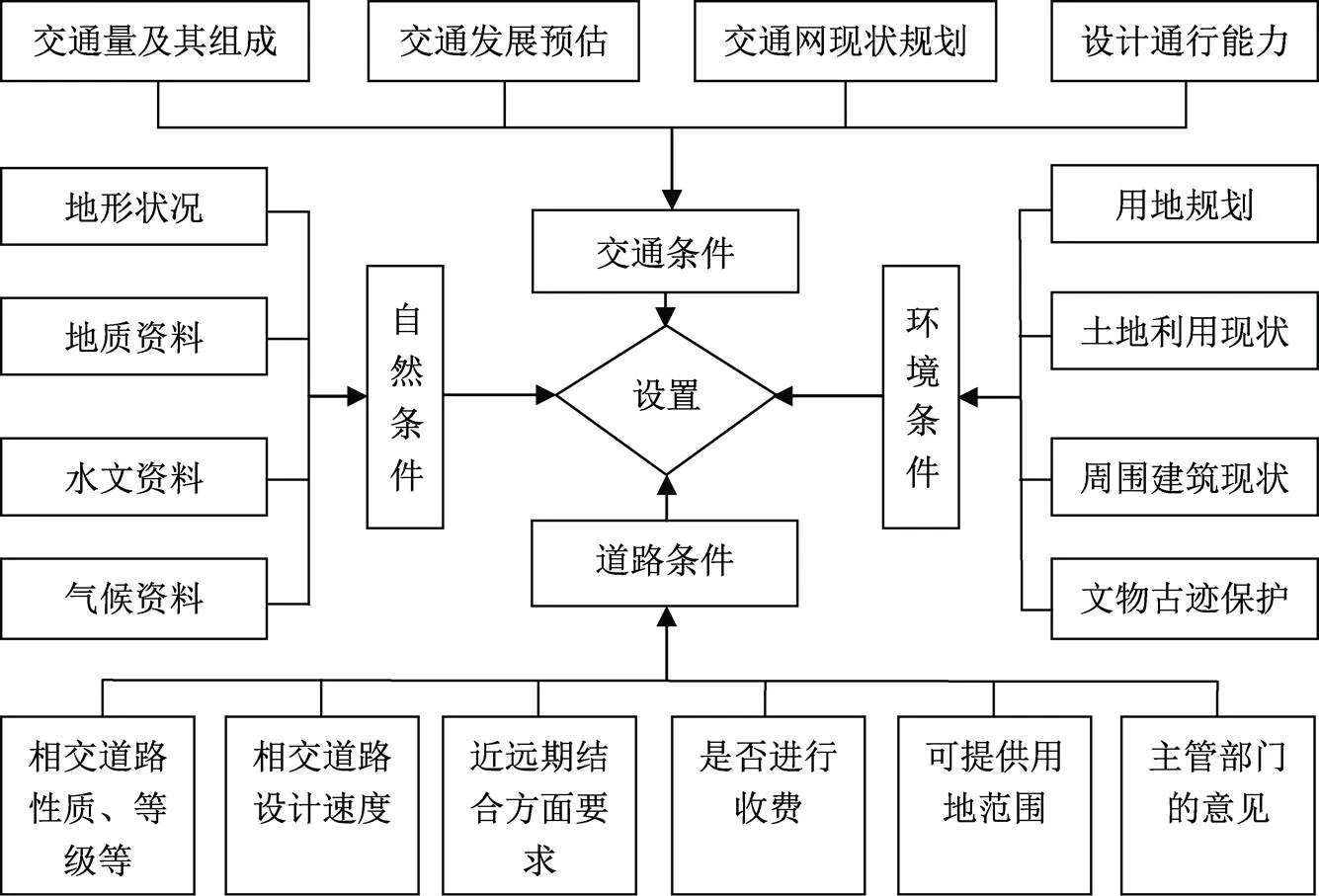
图1 立体交叉设置的条件

2 研究区域概况

本工程为永蓝高速公路主线与嘉宁公路的交叉处，位于宁远县禾亭镇和上宜圩交接处，主线设计范围：K94+310~K96+130，标段全长1.82 km。立交为单喇叭式立体交叉，设匝道收费站一座，二进二出。立交构造物包括：主线跨线桥1座，5条匝道，总长度5440.107 m。E匝道全长1879.343 m。

3 线元法匝道数据计算

3.1 线元类型的判断

由线元法定义可知线元的三种类型有直线、圆曲线和缓和曲线，一般根据输入已知参数起终点的曲率半径的不同，进行线元类型的判断[10]。

设线元起点曲率半径为Rs，终点曲率半径为Re，有[11]：

（1）直线：起点曲率半径等于终点曲率半径，且为无穷大，即Rs=Re=∞；

（2）圆曲线：起点曲率半径等于终点曲率半径，但不为无穷大，即Rs=Re≠∞；

（3）缓和曲线：起点曲率半径不等于终点曲率半径，即Rs≠Re。

3.2 直线坐标正算

直线坐标正算时需要已知线元起点桩号s、起点中桩坐标（s，s）、起点的走向方位角s以及直线长度。

设直线上任意点位的桩号为Z，则j点至起点的线长L为

任意点j的中桩坐标为

3.3 圆曲线坐标正算

圆曲线坐标正算时需要已知线元起点桩号Z、起点中桩坐标（X，Y）、起点的走向方位角α、圆曲线半径、曲线长度以及偏向[12]。

设圆曲线上任意点位的桩号为Z，则点至起点的弧线长度l为

弦长sj的弦切角与弦长为

弦长的方位角与点的走向方位角为

其中正负号的选取为：路线右偏取“+”，路线左偏取“-”后面公式如不注明，正负号选取方法相同。

任意点的中桩坐标为

3.4 缓和曲线坐标正算

缓和曲线坐标正算时需已知线元起点桩号Z、起点中桩坐标（X，Y）、起点走向方位角α、起点曲率半径R、终点曲率半径R、缓和曲线长度以及偏向[13]。

缓和曲线根据线元起终点半径的大小可分为：正向缓和曲线（R>R）和反向缓和曲线（R<R）。正向缓和曲线又分为：正向完整缓和曲线（R<R=¥）和正向非完整缓和曲线（R<R≠¥）；同理，反向缓和曲线可分为：反向完整缓和曲线（R<R=¥）和反向非完整缓和曲线（R<R≠¥）。因为完整缓和曲线是非完整缓和曲线的特例，所以在设计时，可直接用非完整缓和曲线计算公式线进行计算[14]。

（1）正向非完整缓和曲线坐标正算

设正向非完整缓和曲线原点¢到缓和曲线起点的曲线长为l，则原点¢至终点的曲线长度为

缓和曲线参数为的计算公式为

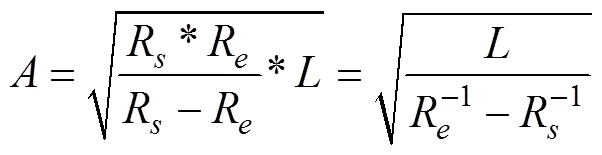
设缓和曲线上任意点的桩号为Z，有

将l、l代入

得到起点的切线支距坐标（x¢，y¢）和点的切线支距坐标（x¢，y¢）。弦长的长度以及在切线支距坐标下的方位角为

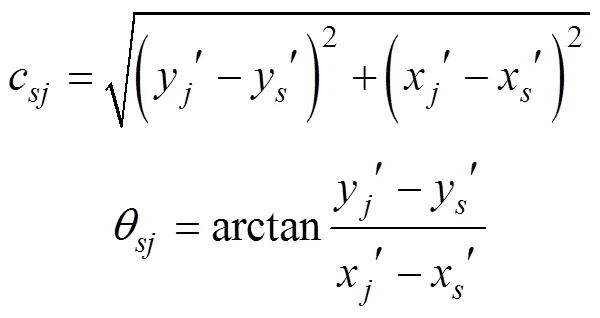
点的偏角和点的偏角为

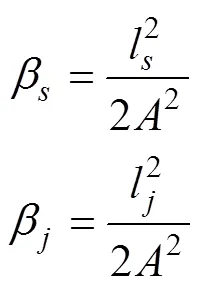
弦长在点的弦切角为

弦长的方位角与的走向方位角为

任意点j的中桩坐标为

（2）反向非完整缓和曲线坐标正算

设反向非完整缓和曲线原点¢到缓和曲线终点的曲线长为l，则原点¢至起点的曲线长度为[15]

缓和曲线参数为，的计算公式为

设缓和曲线上任意点的桩号为Z，有

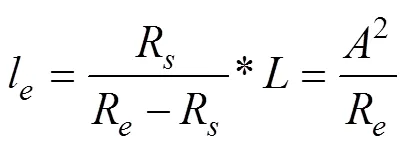
将l、l代入

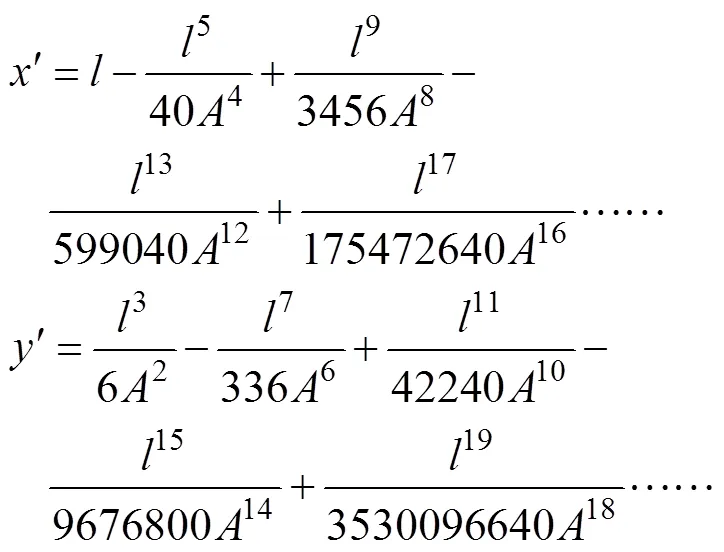
得到起点s的切线支距坐标（x¢，y¢）和点的切线支距坐标（x¢，y¢）。弦长的长度以及在切线支距坐标下的方位角为

点的偏角和点的偏角为

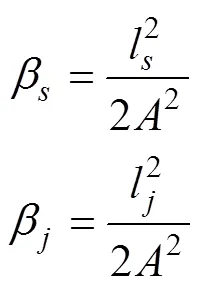
弦长在点的弦切角为

弦长的方位角以及点的走向方位角为

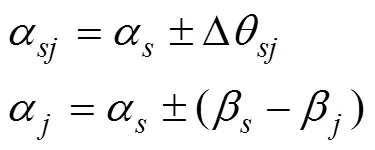
任意点的中桩坐标为

3.5 匝道主点桩号与坐标计算

在计算出了匝道任意点的中桩坐标（X，Y）后，还需要根据路线宽度计算左右边桩的坐标。设点中桩距左边桩距离为，距右边桩距离为，点走向方位角为α，则α-90°为点到点左边桩的方位角，αj+90°为点到点右边桩的方位角[16]，故左边桩坐标计算公式为

右边桩计算公式为

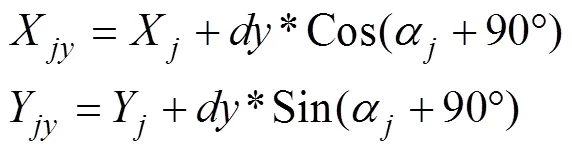
这里通过对宁远东互通式立交桥A匝道上点位的测量，并对测量结果进行坐标计算，如表1所示。

表1 E匝道边桩点坐标

Tab.1 E-ramp edge pile point coordinates

4 匝道主坐标计算反算

4.1 直线坐标反算

直线坐标反算时，需要已知起点的桩号Z，坐标（X，Y）以及走向方位角α。

设点为直线附近任意边桩点，坐标为（X，Y），点对应中桩点为，直线的点斜式方程为

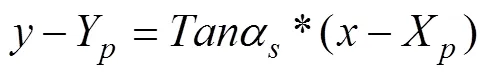
将起点的中桩坐标代入得

因为直线⊥，所以有

合并式（29）和式（30）得

整理后得点坐标为

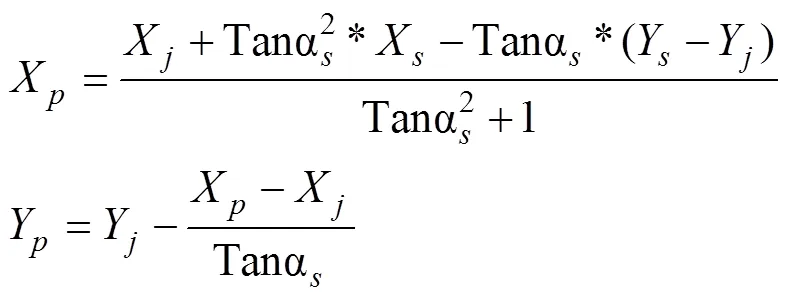
点桩号与走向方位角为

4.2 圆曲线坐标反算

圆曲线坐标反算需已知起点的桩号Z，坐标（X，Y），走向方位角α，曲线半径以及线路偏向。

设（X，Y）为圆曲线附近任意边桩点位，圆曲线圆心点的方位角为

圆心点的坐标为

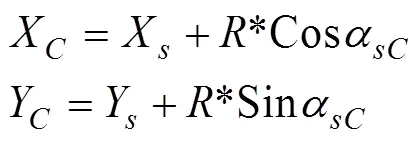
由、两点坐标计算出直线的距离和方位角为

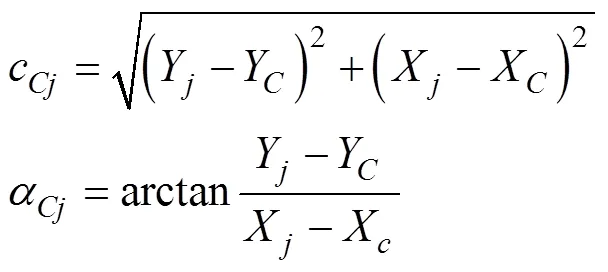
则点距中桩点的距离为

由圆心坐标反算垂足点的中桩坐标为

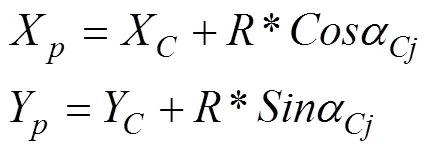
起点到点的的弦长与弦切角为

故p点的桩号和走向方位角为

4.3 缓和曲线坐标反算

缓和曲线坐标反算需已知起点的桩号Z，坐标（，），走向方位角α，终点坐标（X，Y），起点曲率半径R，终点曲率半径R，缓和曲线长度L以及线路偏向。

以=2 min（R，R），即起终点半径最小值的二倍为半径作圆弧，该圆弧称为缓和曲线的拟合圆弧。

（1）拟合圆弧圆心坐标计算

设弦长的中点为，拟合圆弧圆心为，有

弦长的弦长以及方位角为

直线的距离以及方位角为

则拟合圆弧圆心的坐标为

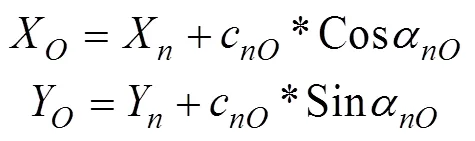
拟合圆弧弦长在起点的弦切角以及拟合圆弧长为

缓和曲线长与拟合圆弧长之差为

（2）垂足点初始桩号及其改正数的计算

设点为缓和曲线附近任意边桩点，坐标为（X，Y），直线的长度及其方位角为

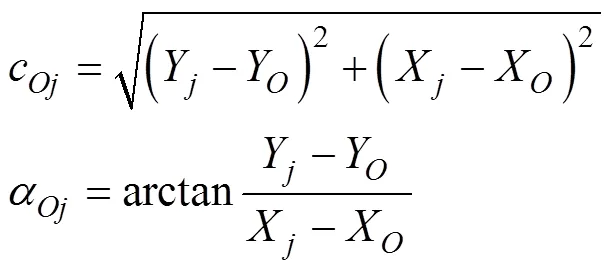
边桩点在拟合圆弧上垂足¢点的坐标为

在拟合圆弧上，弦长¢的弦切角及¢拟合圆弧长度为

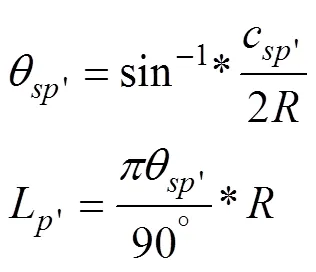
则缓和曲线垂足点桩号的初始值为

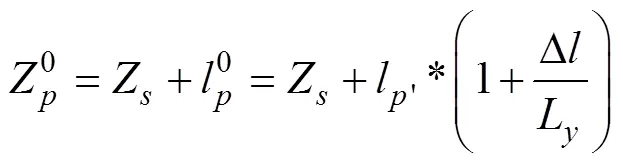
式中0为缓和曲线起点至初始桩号垂足点0的线长，称为初始线长。对初始桩号经坐标正算可计算初始桩号垂足点的坐标（0，0），走向方位角0。

直线0的长度及方位角为

边距0以0走向方位角α为零方向的走向归零方向为

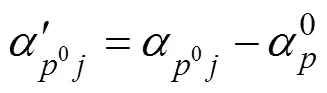
走向归零方向的标准值，左边桩应为270°，右边桩应为90°，故偏角改正数为

当>0时，垂足点初始线长0的改正数>0，当<0时，改正数<0。

缓和曲线初始线长改正数为

（3）改正后垂足点桩号及垂线方程残差值的计算

改正后垂足点桩号为

再由Z经坐标正算计算出垂足点中桩坐标（X，Y）以及走向方位角α。将其代入垂线方程残差计算公式

得垂线方程残差值(l)，如果|(l)|<0.001 m，则计算结束，否则再计算一次。

这里通过对宁远东互通式立交桥A匝道上点位的测量，并对测量结果进行坐标反算。（表2）

表2 A匝道边桩点坐标反算表

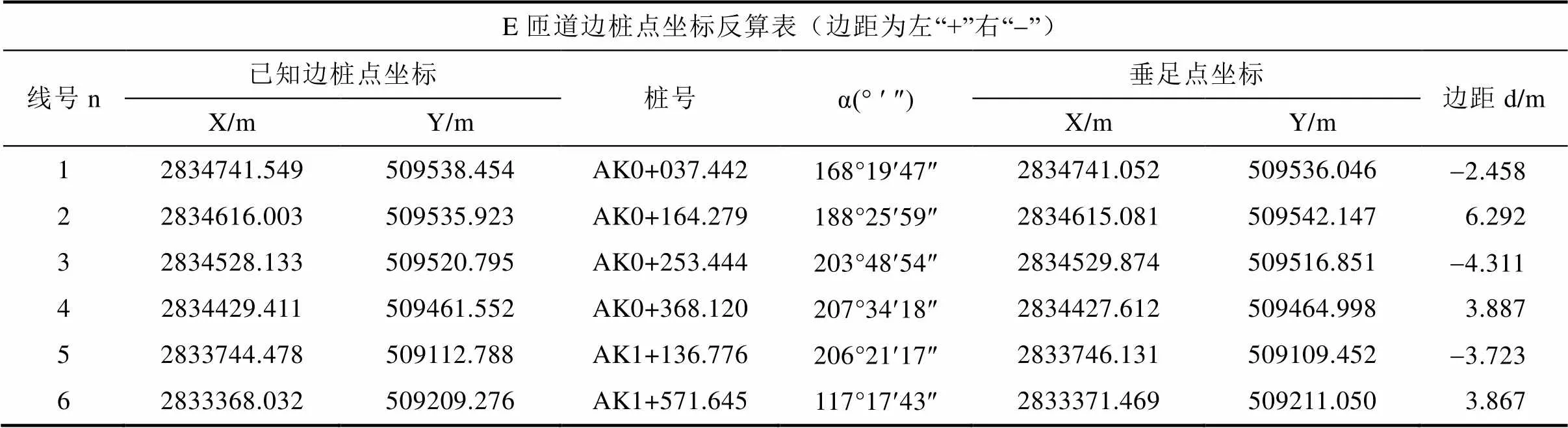
Tab.2 A Inverse coordinates of ramps and piles

5 程序设计界面及使用说明

本程序是采用C#软件对线元法进行编制的，可以实现匝道坐标正反算及边桩坐标的计算，同时可以导入输入数据以及对计算结果进行保存，如图2所示。

在坐标正算时，首先根据图纸设计输入起点桩号、走向方位角、起点中桩坐标以及需要计算的线元个数。然后根据图纸设计，依次输入每个线元的起点曲率半径，终点曲率半径、线元长度与偏向，当线元起终点曲率半径为无穷大时，在对应半径栏输入0；当线元左偏时，在对应偏向栏输入-1；线元右偏时，在对应偏向栏输入1；线元为直线，在对应偏向栏输入0。所有线元输入完成并检查无误后，点击计算，便可计算出各个线元的终点桩号、坐标与走向方位角。

当需要计算线路任意桩号中桩及边桩坐标时，在“加桩坐标计算”栏输入需要计算的桩号、左右边桩距中桩的距离，点击计算，便可计算出相应中桩的坐标、走向方位角，左右边桩的坐标。

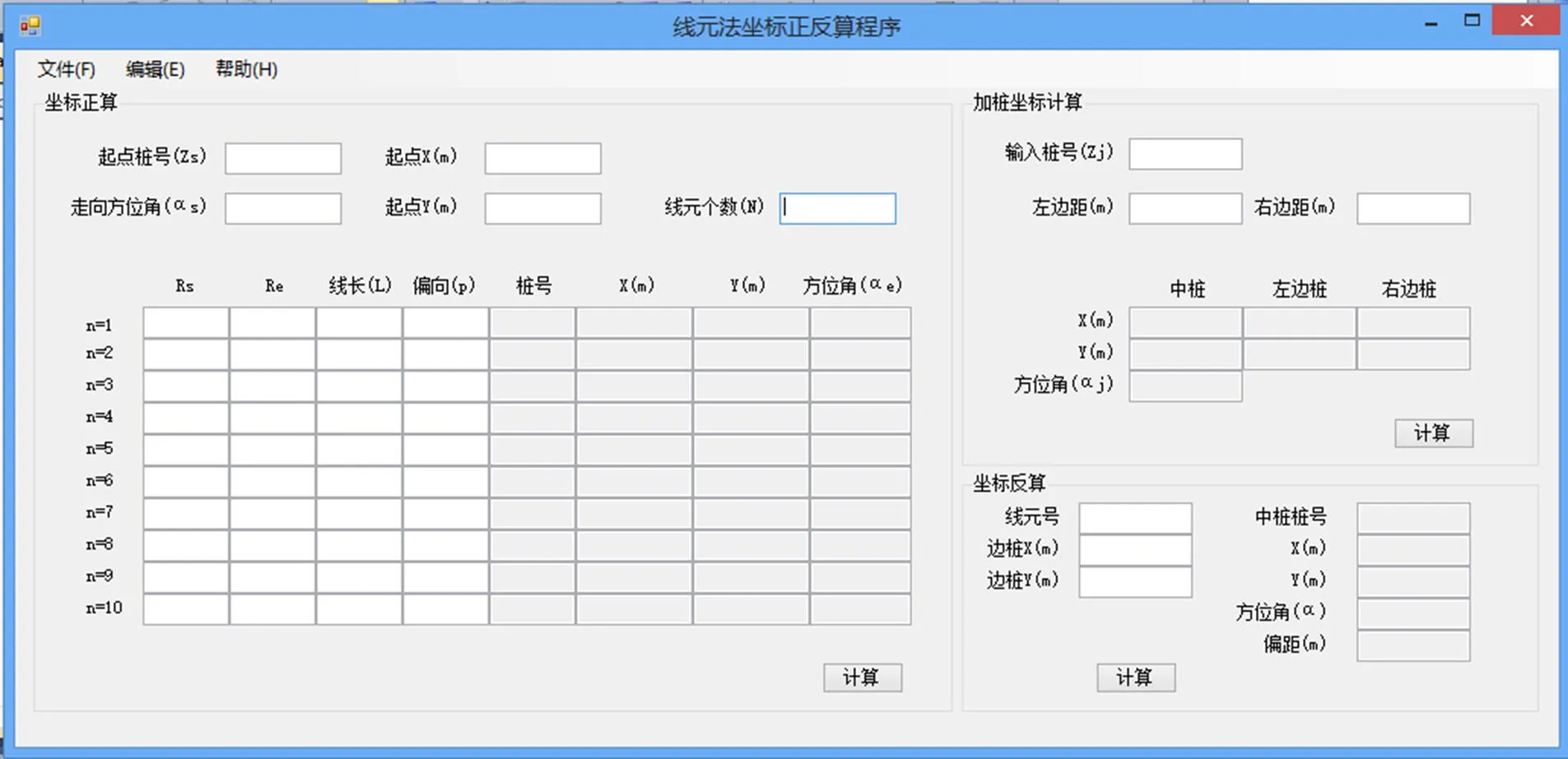
图2 匝道坐标计算程序界面图

当知道某线元段内一个边桩点的坐标，欲反算求其中桩的桩号、坐标以及距中桩的距离，可在“坐标反算”栏内计算。先输入该点所在的线元号和坐标，点击计算，便可计算出所需要的结果。

6 结束语

本文是从互通式立交桥组成与条件的方向展开研究，确定了对各匝道中边桩点位放样数据，并且通过C#语言编写匝道坐标计算程序，并对各匝道中边桩点位放样数据进行了计算与检核，验证了程序计算的可靠性。从而为桥梁匝道的计算提供了方便，提高了工程的效率。

[1] 潘兵宏. 多路互通式立体交叉的形式[J]. 长安大学学报(自然科学版), 2002(4): 33-35.

[2] 孙兴波. 城市道路立交选型方案评价研究[D]. 长沙理工大学, 2012.

[3] 覃辉. 缓和曲线坐标反算的直接解算法[J]. 勘察科学技术, 2010(5): 20-25.

[4] 王明刚. 适于山区条件高速公路互通立交类型及模式的研究[D]. 重庆交通大学, 2010.

[5] 吕森. 城市道路与立体交叉[J]. 商业文化(下半月), 2012(12): 363-363.

[6] 钱成会. 互通式立交交通适应性研究[D]. 长安大学, 2012.

[7] 王彬. 对道路与铁路立交设计的研究[J]. 铁道建筑, 1996(2): 25-27.

[8] 覃辉. CASIO fx-5800P编程计算器公路与铁路施工测量程序[M]. 上海: 同济大学出版社, 2009: 49-62.

[9] 高速公路丛书编委会. 高速公路立交工程[M]. 北京: 人民交通出版社, 2001: 75-107.

[10] 吴国雄, 李方. 互通式立交设计范例[M]. 北京: 人民交通出版社, 2001: 1-7.

[11] 张小璞, 左小清. 在ArcGIS下基于Python的路网数据批处理方法[J]. 软件, 2018, 39(7): 130-133.

[12] 陈艳艳, 黄义忠. 基于全排列多边形图示指标法的昆明市土地集约利用评价[J]. 软件, 2018, 39(7): 138-142.

[13] 何志斌. 昆明市主城区热岛效应特征及驱动机制分析[J]. 软件, 2018, 39(7): 152-156.

[14] 刘翔宇, 朱大明. Arcgis中基于Python的地理数据库批量合并方法研究[J]. 软件, 2018, 39(7): 161-165.

[15] 周洲, 侯开虎, 张慧等. 基于. NET平台的物料管理系统的设计与实现[J]. 软件, 2018, 39(7): 177-181.

[16] 朱东红, 吴东丽, 郭剑, 等. 气象自动观测集成平台设计[J]. 软件, 2018, 39(7): 182-190.

Design of Lofting Plan for Overpass Ramp

MA Yi-chao, MI Hong-yan, ZHONG Kai

(Faculty of land and Resources Engineering, Kunming University of Science and Technology, Kunming 650093, China)

This paper studies the design of the overpass measurement scheme, and to the Far East Nanjing interchange as an example in the overpass project construction, measurement personnel need to do the work and the arrangements for the measurement work. Finally, through the design and application of the coordinate calculation software for the middle and side piles of the ramp, the relevant calculation and inspection of the measured lofting data are carried out.

Interchange bridge; Coordinate calculation; Lofting data; Check the core

TP7

A

10.3969/j.issn.1003-6970.2018.12.049

米鸿燕(1963-)，男，昆明理工大学，副教授，主要研究方向：水下地形测量与变形检测；马义超(1993-)，男，昆明理工大学，研究生，主要研究方向：变形监测；钟凯(1995-)，男，昆明理工大学，研究生，主要研究方向：3s集成与应用。

马义超，米鸿燕，钟凯. 立交桥匝道放样方案设计[J]. 软件，2018，39（12）：215-221