KM教学法在离散数学中的应用

田 毅，贾永旺

（内蒙古工业大学 数据科学与应用学院，内蒙古 呼和浩特 010051）

0 引 言

离散数学是大学计算机相关专业的一门重要课程，主要研究离散量的结构和相互间的关系,包括数理逻辑、集合论、代数系统、组合数学、图论、初等数论、离散建模学等内容，所涉及的概念、定理、法则和方法在软件工程、数据结构、编译原理、计算机网络、计算机图形学、数据库原理、人工智能等诸多课程中都有应用，为学习计算机科学与技术的后续课程奠定理论基础，对培养学生计算机思维、分析问题和解决问题的能力起着重要作用。从某种程度上说，学好离散数学就等于开启计算机科学与技术领域的大门。

1 离散数学课程教学现状

目前多数高校采用传统的多媒体或板书授课方式讲解离散数学课程，课堂上教师重点考虑的是自己的“讲述”，往往忽略学生对知识的感知、消化和吸收这个过程。在这种教学模式下，许多学生觉得离散数学就是一门平常数学课，定义多、定理多、概念抽象、理论性强、枯燥乏味，课上听不懂，课下不会做题，到最后也就不听不做了；有的学生觉得课程实用价值较小，在日常生活或其他课程的学习中很少用到，因而学习积极性也不高，久而久之产生厌学情绪，导致这门课程的教学效果往往不理想。

以内蒙古工业大学数据科学与应用学院的信息与计算科学专业为例，该课程安排在大学一年级第一学期，共56学时，选用的教材是高等教育出版社屈婉玲、耿素云和张立昂出版的《离散数学》第1版[1]以及配套参考书《离散数学学习指导与习题解析》。要在56学时内讲完书中19章的内容是不现实的，根据本专业其他课程开设时间和内容以及专业的培养目标，第11章（格与布尔代数）、第18章（支配集、覆盖集、独立集、匹配与着色）省略不讲，第10章（群与环）、第19章（初等数论）在高等代数课程中会详细介绍，第12章（基本的组合计数公式）属于概率论与数理统计课程中的内容。根据以上情况，教学内容学时分配为第1部分数理逻辑，24学时；第2部分集合论，20学时；第3部分代数系统，4学时；第4部分图论，8学时。

鉴于授课过程中发现的以上问题，我们应采取有效措施进行改进，尽量调动学生学习的主观能动性，提高教学效率。KM 教学法目前已应用到C语言程序设计、数据结构、高等数学等课程[2-4]的教学中，实践表明 KM 法可以显著地提高学生的学习积极性和学习效率，这对于其他课程的教学改革具有很好的示范作用。

2 KM教学法的应用

KM 教学法首先是由北京科技大学的杨炳儒教授提出的，K代表的是Knowledge Logic Structure （知识逻辑结构），知识逻辑结构主要用“知识逻辑结构图（KLSG）”表示，它给出课程知识系统的总体架构，从宏观层面展示知识体系，使学生从总体上“着眼”教学内容，从而对知识脉络有比较清晰的认识。M是Mind Mapping（思维导图），思维导图的作用是从微观层面体现课程的知识。KM教学法的主要思想是首先建立知识的逻辑结构框架，然后逐步融入思维导图，最后形成一个集成综合的、逐步递阶的知识逻辑体系。

KM教学法可归结为“抽点—连线—成网—扩展—嵌入”5个过程。以离散数学第1部分数理逻辑（命题逻辑基本概念、命题逻辑等值演算、命题逻辑的推理理论、一阶逻辑基本概念、一阶逻辑等值演算与推理）为例，阐述KM教学法在离散数学课程教学中的实施过程，数理逻辑内容的知识逻辑结构图如图1所示。

由图1可知，数理逻辑可分为命题逻辑和一阶逻辑两部分内容，命题逻辑的内容分为基本概念、等值演算和推理理论3方面，而一阶逻辑的内容也对应地分为基本概念、等值演算和推理理论3方面， KLSG让数理逻辑的研究内容一目了然。

1）抽点。

抽点就是将教学内容按章节从特殊到一般的方式进行解析，通过分析，把每部分的定义、定理、法则、理论等抽象出来，舍去不重要的细节部分。离散数学中数理逻辑部分的抽点如下。

第1章：命题的定义、命题的符号化、否定联结词、析取联结词、合取联结词、蕴含联结词、等价联结词、命题公式、真值表法、重言式、矛盾式、可满式。

第2章：等值式的定义、等值式模式、等值演算、合取范式、析取范式、极大项、极小项、主合取范式、主析取范式。

第3章：推理的定义、证明推理正确的定理、自然推理系统P、推理的3种证明方法（一般证明方法、附加前提证明法和归谬法）。

第4章：命题的一阶逻辑符号化、个体词、谓词、量词。

第5章：一阶逻辑等值式的定义、一阶逻辑中的基本等值式、前束范式、一阶逻辑推理的形式结构、推理定律、一阶逻辑推理系统 。

2）连线。

连线即分析第1步抽点得到的定义、定理、法则和理论之间的内在联系，将其有机地串联形成“知识链”，原则是从“局部到整体”，从某个概念或例子开始，按照认识事物的一般规律，由表及里，由外向内，把抽点及抽点相关的内容有机联接起来，从而形成一个整体的、具有逻辑关系的知识链。

以命题逻辑的基本概念为例，其知识链为：首先通过实例引入“命题的定义”；其次谈命题的分类，命题可分为简单命题和复合命题，简单命题可以由小写英文字母表示，而复合命题符号化的时候，可分解为简单命题和联结词两部分，联结词的符号化又可以引入5种联结词的定义及符号化，这样，任意一个命题都可以符号化为命题公式；最后，由赋值的定义引入命题公式真值表的概念，由真值表最后一列的情况引出重言式、矛盾式、可满式的概念。这样就把第1步抽点得到的各“点”有机串接在一起，从而形成一个知识链即思维导图，如图2所示。

3）成网。

成网即分析并且将第2步连线中的各知识点横向、纵向地联系起来，从而形成一个知识网，数理逻辑部分1、2、3章形成的知识网如图3所示。

4）扩展。

扩展即以第2步、第3步得到的知识链和知识网为基础，本着由浅入深、由简到繁、由特殊到一般的知识的学习规律，教师沿着脉络详细地讲授各部分的难点和重点，并且依据实际需要补充一些相关内容，如在第1章，教师讲完5种联结词的定义及符号化后，还可以扩展到“或非联结词”和“与非联结词”的内容；讲完第2章命题的等值演算后，还可以再讲“可满足行问题与消解法”。扩展步骤一方面可以开阔学生的眼界，另一方面可以让教学保持上升态势。

5）嵌入。

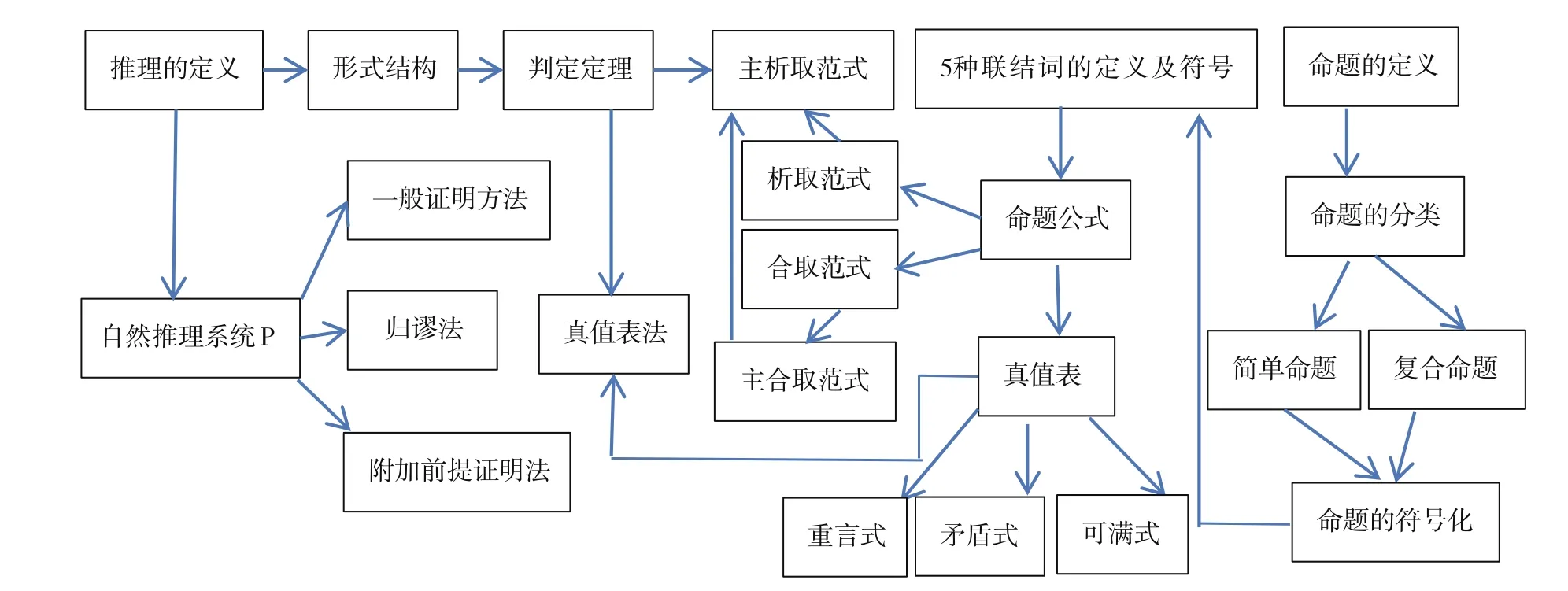
图3 数理逻辑部分1、2、3章形成的知识网

无论是知识链还是知识网，都是思维导图。在讲授数理逻辑内容时，教师可以适时地将这些思维导图导入图1的知识逻辑结构图中，以便学生形成知识学习的“薄—厚—薄”3个过程。知识的逻辑结构图仅是内容架构，是简单的；把思维导图逐步导入KLSG图中后，内容就变厚了；经过比较、总结和归纳，知识会再次变薄，再和最初的KLSG进行比对、融合。经过这个过程，学生对知识的整体、局部及脉络都会有较深刻的认识。

3 结 语

以内蒙古工业大学数据科学与应用学院的信息与计算科学专业为例，信计17—1、2班采用KM教学法讲授离散数学这门课程，学生普遍反映对课程知识的轮廓、脉络掌握得比较清晰，在期末考试前，依照各章节的“知识逻辑结构图”和“思维导图”很轻松地进行复习，考试取得了良好成绩，及格率在90%以上；而信计17—3、4班采用普通教学法讲授这门课程，教学效果明显不如信计17—1、2班，由此也可以看出KM教学法可有效地提高教学效率。