飞蛾火焰优化算法及其在梯级水库优化调度中的应用

郭 荣，崔东文

(1.云南省文山市水务局,云南 文山 663099；2.云南省文山州水务局,云南 文山 663000)

实行梯级水库群优化调度，不但可以在不增加额外投资的情况下增加发电量以提高经济效益，而且可以保证电力系统的安全稳定运行和水能资源的充分利用，具有十分重要的现实意义[1-2]。由于梯级水库群优化调度属多约束、高维度、非线性、多阶段组合优化问题，至今没有通用高效的求解方法。目前，除传统线性和非线性方法、逐步优化算法、动态规划法等方法用于求解梯级水库群优化调度模型外，群体智能优化算法(SIA)由于具有自学习、自组织、自适应的特征和简单、易懂、鲁棒性强以及并行处理等优点已广泛用于梯级水库群优化调度，并取得了一定的实际应用效果，如粒子群优化(PSO)算法[3-4]、人工鱼群算法(AFSA)算法[2,5]、蚁群算法(ACO)算法[6-7]、群居蜘蛛优化(SSO)算法[8]、布谷鸟搜索(CS)算法[9]、混合蛙跳算法(SFLA)[10-11]、狼群算法(WPS)[12]、鸟群算法(BSA)[13]和鲸鱼优化算法(WOA)[14]。群体智能算法是模拟自然界生物群体的社会行为而构造出的一类概率搜索算法，算法计算简单、易于实现，目前已在水利及各行业领域得到广泛应用。

为进一步拓展群体智能算法在梯级水库群优化调度中的应用范畴，本文将飞蛾火焰优化(Moth-Flame Optimization，MFO)算法应用于某梯级水库群优化调度求解，并将求解结果与SFLA、PSO、CS和IWO算法的求解结果进行对比分析，以验证MFO 算法在梯级水库群优化调度模型求解中的可行性和有效性。

1 飞蛾火焰优化算法

飞蛾火焰优化(MFO)算法是文献[15]基于模仿飞蛾捕焰行为提出的一种新型群体智能仿生算法，具有调节参数少、极值寻优能力强和鲁棒性好等特点。文献[15-17]证明了该算法性能整体上优于PSO等传统优化算法。参考文献[15-18]，MFO算法搜索寻优过程可描述如下。

a) 捕焰行为。第i只飞蛾Mi基于自身趋光性，感知火焰群中离自身最近且较优的第j个火焰Fj，其模仿对数螺旋飞行路径的飞蛾-火焰位置更新算子描述：

S(Mi,Fj)=Di·ebt·cos(2πt)+Fj

(1)

式中Mi——第i只飞蛾；Fj——第j个火焰；S——螺旋函数；Di——第j个火焰到第i只飞蛾的距离，表示为Di=|Fj-Mi|；b——螺旋形状常数；t——[-1,1]之间的随机数。

b) 弃焰行为。在迭代更新时，适应度值较差的火焰会变被飞蛾丢弃，火焰总数在自适应减少，让飞蛾收敛于同一火焰中，使MFO算法获得较快的收敛速度，公式：

(2)

式中l——当前迭代次数；N——最大火焰数量；T——最大迭代次数。

2 水库优化调度模型

2.1 目标函数

以发电量E最大为优化调度目标的数学模型可表示为[13-14]：

(3)

式中Ai——第i个电站出力系数；Qit——第i个电站第t时段的平均发电流量，m3/s；Hit——第i个电站第t时段的平均发电水头，m；R——水电站总数目；T——总时段数(本文计算时段为月，T=12)；ΔT——时段长度。

2.2 约束条件

水位约束：

Zit,min≤Zit≤Zit,max

(4)

流量约束：

Qit,min≤Qit≤Qit,max

(5)

水库水量平衡约束：

Vit+1=Vit+(qit-Qit-Sit)ΔT

(6)

出力约束：

Ni,min≤Ni≤Ni,max

(7)

式中Zit,min、Zit,max——第i个电站第t时段最低和最高限制水位；Zit——第i个电站第t时段的平均库水位；Qit,min、Qit,max——第i个电站第t时段最小与最大发电流量；Vit+1、Vit——第i个电站第t时段初水库蓄水量；qit——第i个电站第t时段的平均入库流量；Sit——第i个电站第t时段的弃水流量；Ni,min、Ni,max——第i个电站最小与最大限制出力。

目前对该模型中的约束条件普遍采用罚函数法和搜索空间限定法两种处理方式，本文参考文献[13-14,19]采用搜索空间限定法处理模型中的约束条件。

3 MFO算法求解梯级水库优化调度步骤

参考文献[16-18]，MFO算法求解梯级水库群优化调度步骤可归纳如下。

Step1划分梯级水库群调度期时段，确定决策变量及其取值范围。

Step2由于MFO算法是求解极小值，因此确定式(3)的倒数作为MFO算法求解梯级水库群优化调度的适应度函数，表示为式(8)：

(8)

Step3参数设置。设置MFO算法飞蛾种群规模n、最大迭代次数M、搜索空间维数d(d=R×T)以及最大火焰数量N，令当前迭代次数l=0。

Step4位置初始化。将各时段末水库水位Z1、Z2、…ZRT看成R×T维决策空间飞蛾个体的位置X1、X2、…XRT，在水位取值解空间范围内初始化飞蛾位置。

Step5利用式(8)计算飞蛾个体适应度函数值，判断算法是否满足终止条件，若满足则转至Step8，否则执行Step5。

Step6利用式(2)更新火焰数量；利用式(1)更新飞蛾-火焰位置。通过式(8)计算飞蛾个体适应度函数值，保存飞蛾及火焰空间位置。

Step7找到当前最好火焰个体空间位置，判断算法是否满足终止条件，若满足则转至Step8，否则令l=l+1，并执行Step5—7。

Step8输出最优火焰个体空间位置及全局极值，即火焰最终所处的空间位置即为梯级水库群优化调度最佳决策变量，算法结束。

4 实例分析

本文以某梯级水库群优化调度问题求解为例验证MFO算法用于水库群优化求解的可行性和有效性，并与SLFA、PSO、CS和IWO算法进行比较。算法参数设置如下：①5种算法最大迭代次数M均设置为200，MFO、SLFA和PSO算法种群规模N均设置为50，其中，SLFA算法子群数K=5，子群内青蛙个数N=10，子群数局部进化次数T1=10；②PSO算法惯性权重系数ω=0.729，局部、全局学习因子c1=c2=2.0；③CS算法鸟窝位置数n=25、发现概率pa=0.25；④IWO算法种群Ps=10，族群Qs=25，最大、最小可生成种子数Smax和Smin分别为5和0，非线性指数m=3，σ0=0.5，σf=0.001。

该梯级水库由于水库A和水库B组成，数据来源见文献[14]。依据上述梯级水库群优化调度求解步骤，以年发电量最大为准则(优化目标为1/E)，利用MFO、SLFA、PSO、CS和IWO算法计算水库A和水库B丰、平、枯各月月末水位(决策变量为24维)，使该梯级水库在调度期内发电量最大。为验证各算法的极值寻优能力和稳健性能，各丰、平、枯调度模型均进行连续10次求解，求解结果见表1—3，5种算法寻优过程线见图1—3。

a) 从表1—3来看，MFO算法丰、平、枯优化调度发电量(10次均值)分别为55.950 5、37.779 3和25.169 6亿kW·h，分别比其他4种算法增加了0.179 2～0.960 2、0.097 2～0.564 1、0.082 4～0.322 0亿kW·h，具有较好的优化调度效果。从优化调度结果来看，MFO算法丰、平、枯各10次的求解结果均相同，表明MFO算法不但具有较好的寻优精度和极值寻优能力，而且具有较好的收敛稳定性。

表1 丰水年5种算法梯级水库优化调度发电量结果 亿kW·h

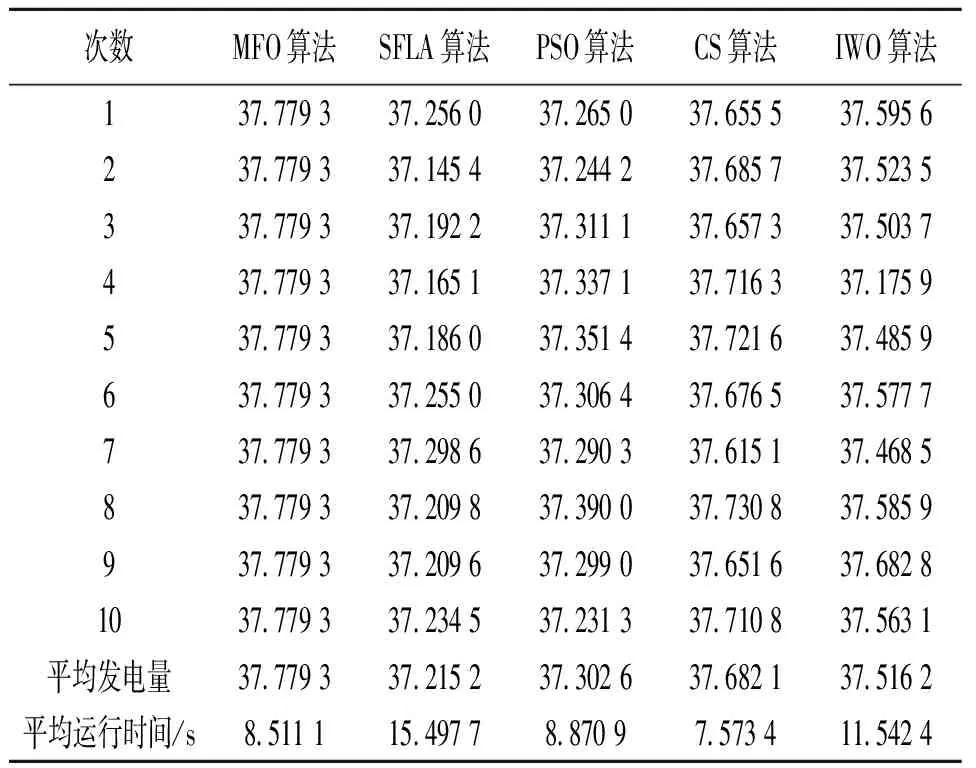
表2 平水年5种算法梯级水库优化调度发电量结果 亿kW·h

表3 枯水年5种算法梯级水库优化调度发电量结果 亿kW·h

从平均运行时间来看，MFO算法在平水年和枯水年优化调度中略劣于CS算法，但要优于其他3种算法，具有较快的运行时间。

b) 从图1—3来看，MFO算法不但求解精度高于其他4种算法，而且具有较快的收敛速度。在丰、平、枯进化过程中，MFO算法迭代至70代左右时便收敛到相对全局最优解，相对而言，CS算法和SFLA算法收敛速度较慢。

c) 整体而言，5种算法最终优化调度结果由优至劣依次是MFO、CS、IWO、PSO和SFLA算法。

5 结语

介绍了一种新型群体智能仿生算法——飞蛾火焰优化(MFO)算法，给出了梯级水库群优化调度问题求解的MFO算法设计及求解步骤。为验证MFO算法在梯级水库群优化调度问题求解中的可行性和有效性，将该算法应用于某梯级水库中长期优化调度实例问题的求解，求解结果与SFLA、CS、PSO和IWO算法的求解结果进行验证比较。验证表明：MFO算法丰、平、枯优化调度发电量分别比SFLA 、CS、PSO和IWO算法增加了0.179 2～0.960 2、0.097 2～0.564 1、0.082 4～0.322 0亿kW·h，具有运行速度快(仅次于CS算法)、收敛精度高、极值寻优能力强以及收敛稳定性好等特点。本文提出的模型及方法不但拓展了群体智能算法在梯级水库群优化调度模型求解中的应用范畴，而且为MFO算法求解复杂、高维的梯级水库群优化调度模型提供了一种新的途径和方法。