基于水量平衡方程的水库调洪演算基础数据误差传播规律研究

周 斌

(汕尾市水利水电规划设计院，广东 汕尾 516600)

为确定水库洪水位，需要根据水量平衡原理进行水库调洪演算。由于方程各项积分难以直接计算，需要时间分段、逐时段连续求解，工程中常采用梯形法进行单步时段积分。有诸多学者尝试了Runge-Kutta法、Lagrange插值[1]、三次样条插值函数[2]等诸多数值方法以提高单步时段积分的精度。笔者曾对梯形法的积分误差和传播进行了讨论，提出了最大可能误差的计算方法[3]以控制计算误差风险。入库洪水、泄洪能力和库容的基础数据如存在误差，也将直接影响到计算的调洪成果精度，曾有学者对以上三者随机过程产生的蓄洪量的特性进行了相关研究[4]。近年来随着洪水预报技术的发展，不少学者也开展了基于水文预报的调洪演算研究[5]。因此，分析基础数据误差对调洪成果精度的影响是必要的。

1 调洪演算的水量平衡基本方程

对任一时段(如t1→t2)，入库水量减去出库水量，等于该时段内水库增加或减少的蓄水量[5]，此时水库水位由z1升降至z2，需满足水量平衡方程：

(1)

式中Q(t)——入库流量过程；q(z(t))——出库流量过程；F(z)——水库库面面积；z(t)——库水位随时间的变化过程。

采用梯形数值积分法[6]，式(1)可改写为常见的实用公式(以下称实用水量平衡方程)：

(2)

式中Qt1、Qt2——时段始、末的入库流量；qz1、qz2——时段始、末的出库流量；Vz1、Vz2——时段始、末的库容；Δt——计算时段，Δt=t2-t1。

2 时段内的单步误差方程及单步误差传递规律

2.1 单一时段内的水位变化量

式(2)为非线性方程，已知时段初的库水位z1可以直接解得时段末的库水位z2。为方便后续讨论，先讨论一个近似解答。

(3)

2.2 入库洪水误差产生的时段末水位单步误差方程

在计算时段(如t1→t2)内入库洪水流量存在相对误差ξQ，即入库洪水流量可表述为(1+ξQ)Q(t)。由于误差的存在，将使时段末水位产生误差εQ-z 2(相对误差为ξQ-z2)，即时段末的水位为z2+εQ-z2。则式(2)变为：

(4)

将式(4)采用一阶泰勒公式在z2处展开，并略去高阶微量，可写为：

(5)

式(5)中消去式(2)，整理后有：

(6)

(7)

2.3 泄洪能力误差产生的时段末水位单步误差方程

如出库流量(泄洪能力)存在相对误差ξq，即出库流量可表述为(1+ξq)q(z)。由于误差的存在，将使时段末水位产生误差εq-z2(相对误差为ξq-z2)，即时段末的水位为z2+εq-z2。式(2)可写为：

(8)

将式(8)采用一阶泰勒公式在z2处展开，并略去高阶微量，可写为：

(9)

式(9)中消去式(2)，整理后有：

(10)

(11)

2.4 库容误差产生的时段末水位单步误差方程

如库容曲线存在相对误差ξV，即库容可表述为(1+ξV)V(z)。由于误差的存在，将使时段末水位产生误差εV-z2 2(相对误差为ξV-z2)，将使得时段末水位变为z2+εV-z2，式(2)可写为：

(12)

将式(12)采用一阶泰勒公式在z2处展开，并略去高阶微量，可写为：

(13)

式(13)中消去式(2)，整理后有：

(14)

(15)

2.5 水位误差敏感性排序

(16)

(17)

(18)

2.6 单步误差传递规律

根据前述方程，基础数据的相对误差会产生单步计算时段末的水位误差，汇总得从基础数据的相对误差传递至时段末的库水位单步误差的规律见表1。

表1 单步误差传递规律

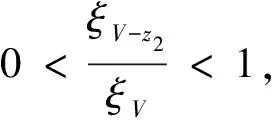
接近库水位极大值(满足Qt1+Qt2=2qz1)处ξQ-z2和ξq-z2存在奇点，且ξQ-z2和ξq-z2在奇点两侧正负号相反。

εV-z2在库水位极大值两侧正负号相反。

εq-z2和εV-z2在库水位极大值点前有交点，交点前|εq-z2|<|εV-z2|。

3 库水位误差累积方程及传播规律

3.1 时段初、末的误差传播基本方程

对任一时段(如t1→t2)，如时段初存在水位误差εz1(初始水位为z1+εz1)，将使时段末的水位变为z2+εz2，有[3]：

(19)

3.2 洪水相对误差产生的水位绝对误差累积方程

水库调洪演算时，第n时段末的库水位总存在相对误差ξQ，可通过式(6)和式(19)计算累积误差，有：

(20)

3.3 出库流量相对误差产生的水位绝对误差累积方程

水库调洪演算时，第n时段末的库水位总存在相对误差ξq，可通过式(10)和式(19)计算累积误差，有：

(21)

3.4 库容相对误差产生的水位绝对误差累积方程

水库调洪演算时，第n时段末的库水位总存在相对误差ξV，可通过式(14)和式(19)计算累积误差，有：

(22)

3.5 累积误差的传播规律

4 算例

某中型水库位于广东省海丰县境内的黄江支流龙船溪上，坝址集雨面积23 km2，主河长9.2 km，河道加权平均坡降1%，枢纽建筑物有1座主坝、5座副坝、溢洪道、2座灌溉输水涵管、2座灌溉进水闸。

溢洪道进口控制段为无闸控制的开敞式宽顶堰， 堰顶高程为12 m，净宽35 m，控制段后接坡度为1∶8的陡槽段，陡槽后接消力池。以堰顶作为起调水位，遭遇洪水时,即从溢洪道自动按最大渲泄能力下泄洪水的调度方式计算遭遇百年一遇洪水的水库调洪过程。为揭示基础资料误差对调洪成果的影响，在调洪成果的基础上直接分析入库洪水偏小10%(ξQ=-0.1)、溢洪道泄流能力偏大10%(ξq=0.1)、库容偏大10%(ξV=0.1)产生的库水位误差情况。调洪过程和水位误差变化过程见图1，最高洪水位附近的误差计算成果摘录见表2。

从误差图可见，水位单步绝对误差在库水位上升期总体上以入库流量的误差影响最显著，出库流量的误差影响最小；库水位降落期则以出库流量误差影响最大，库容误差产生了制约库水位下降的作用；累积水位误差以入库流量误差的影响最为显著，出库流量误差产生了持续了降低库水位的影响；时段相对误差的绝对值仍以入库流量误差影响最大，入库流量和出库流量的相对误差在库水位上升至最高点附近有奇点。入库洪水、泄洪能力和库容三要素的相对误差对该水库最高库水位的影响程度，入库洪水最大、泄洪能力最小。

表2 误差计算成果摘录

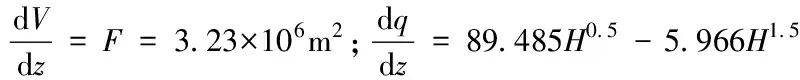
5 结语

采用水量平衡方程调洪演算时，洪水、泄洪能力和库容等原始数据可能存在误差，将影响到计算的调洪成果精度，分析评价这些基础数据误差对调洪成果的影响对工程安全是十分有必要的。各基础数据的相对误差对时段内的水位单步误差有着不同的影响，库水位上升期以入库洪水流量最为敏感，且对库水位相对误差存在放大效应；库水位升、降期，库容误差产生的水位单步误差正负号相反，且相对误差大于0时对库水位相对误差存在缩减效应；最高库水位处入库洪水流量和泄洪能力的水位单步相对误差存在奇点。对于水位传播累积误差，有着不同的影响，在库水位上升期，入库洪水流量最为敏感；库容相对误差大于0时对库水位相对误差仍保持了缩减效应。