基于降水分析的径流代表性研究

郭世兴,肖庆利,刘 艳

(1.陕西省水利电力勘测设计研究院，陕西 西安 710001；2.陕西省渭南市水务局，陕西 渭南 714000)

水文系列是指水文变量按时间顺序排列所形成的数据系列，在时间变化上既有周期性又有随机性[1]，在工程应用和分析时，要满足可靠性、一致性和代表性要求。由于代表段选择直接影响水文计算成果的精准度、工程规模和水文情势预测等，是水资源评价和水文分析计算的基础。对防洪工程，系列代表性偏枯，对工程安全不利；对供水工程，系列代表性偏丰则不利于供水安全；对水资源评价系列选择不当，易造成结果偏差较大。文献[2]要求水文分析计算首先要进行代表性分析。系列的代表性指具有一致性的样本统计特性对总体特性的接近长度，由于总体是未知的，根据数理统计原理，样本系列容量越大，抽样误差分布越集中，其代表性越好，抽样误差越小。

洪水系列代表性目前缺乏有效分析方法，一般通过历史洪水、邻近站长系列对比等途径综合分析[3]。降水(含暴雨)、径流等有较长观测资料时，可通过滑动平均、均值及变差系数的累积曲线等分析趋于稳定的系列长度，还可通过系列的差积曲线变化、时间序列分析等方法确定周期性和丰枯组成。牛文虎[4]从统计参数稳定性分析得出：当资料系列小于30 a时代表性差；大于30 a且小于45 a时代表性较好；大于45 a时代表性好。葛芬莉[5]通过对径流长短系列相对误差对比及不同频率年径流分析，评价径流系列的代表性。文献[6]通过计算样本不同长度的均值和Cv，当数值趋于平稳且连续5 a的变幅在±5%以内时为样本具有代表性的系列长度。王正发[7]利用径流系列时间上的自相似性，采用分形理论的Hausdorff维数分析代表性。目前的代表性研究主要集中在对测站单一水文要素的分析，由于把实测系列假想为总体，采用数理统计方法进行分析，存在均值、Cv无论系列长短(>10 a)均趋近于稳定、模比系数差积最终累积为0的问题，即假定系列为总体来证明样本接近总体的程度。

本文利用水文系列代表性反应各时期不同气候条件下的随机波动性、测站附近流域水文要素呈现同步性的特征，选择在成因上有关联的长系列降水资料，通过周期性分析和长短系列统计特征值分析，综合比较选定具有代表性的降水系列，则同步对应的径流系列也具有代表性，从而避免单纯用径流短系列分析的主观任意性。

1 代表性分析方法

当径流系列较长时，可采用滑动平均、累积平均等方法，分析评价该系列或代表段的代表性，通过了解均值、变差系数分析趋于稳定的系列长度，为代表段选取提供依据；也可通过差积曲线、时间序列分析等，了解系列或代表段系列的周期性及丰、平、枯和连续丰、枯水径流组成来评价其代表性。

1.1 系列代表性分析

流域的变差系数Cv一般比较稳定，可一定程度反应资料的稳定性，Cv随样本的统计年数的增加，数值基本趋于稳定，认为系列代表性好；系列累积平均值计算到一定年限后，其数值波动幅度在5%以内时也认为系列代表性好。系列均值、变差系数Cv的计算公式如下：

式中xi——系列样本值(降水或径流等)；n——系列或样本长度(n≥5)。

1.2 系列丰枯周期性分析

水文系列周期性用差积曲线(即距平累积法)或滑动平均分析。由于模比系数累积平均值计算到一定年限后数值波动幅度很小，趋近于1时认为系列代表性好。一般将逐年(ki-1)从资料开始年份累积到终止年份(顺时序)，绘制逐年模比系数差积值与对应年份的关系线即为模比系数差积曲线；滑动平均值按步长L平滑滤波，滤掉系列中小的波动而突出趋势变化，反映丰、枯段及趋势。模比系数及模数距平累积值、滑动平均值的计算公式如下：

2 工程实例研究

延河是黄河右岸一级支流，发源于榆林白于山南麓，流经安塞县城、延安市，从延川县注入黄河，属黄土丘陵沟壑区。安塞县化子坪以上为延河上游段，无大的水利工程[8]，本次以安塞水文站1981—2015年实测径流量和1953—2015年降水资料为例，研究系列代表性的分析方法。绘制降水量与径流量双累积曲线见图1，累积降水量作为参考变量，受人类活动及降水量共同作用的累积径流量作为基准变量[9]，通过双累积曲线可以看出安塞站降水和径流一致性较好，故延河上游段人类活动对径流量的影响不明显，可以用具有成因关系的降水过程对径流过程进行代表性分析研究。

根据安塞站1981—2015年共计35 a径流实测系列统计结果，多年平均径流量为0.5×108m3，最大年径流量为0.95×108m3(1992年)，最小年径流量为0.25×108m3(1997年)，最丰水年和最枯水年径流量分别是平均年径流量的1.9倍和0.5倍；安塞站1953—2015年共63 a降水量统计，多年平均降水量为462 mm，最大年降水量为851 mm(1964年)，最小年降水量为210.4 mm(1997年)，最大年和最小年降水量分别是平均年降水量的1.84倍和0.46倍。故降水量和径流量的最值与平均值的倍比关系一致。

对径流系列中丰、平、枯水年的组成及距平进行分析得表1，在安塞站1981—2015年的径流系列中，丰、偏丰水年有9 a，占25.7%，平水年有11 a，占31.4%，枯、偏枯水年所占比例偏高，径流系列为偏枯；1953—2015年的降水系列中丰、偏丰水年有16 a，占28%，平水年24 a，占42.1%，枯、偏枯水年17 a，占29.8%，降水系列为丰枯基本对称。从丰枯组成分析可以看出，1953—2015年降水系列比1981—2015年径流系列的代表性好，可以通过年降水系列代表性分析年径流系列的代表性。而单方面用降水资料插补延长径流资料，虽然代表性好但可靠性降低。

表1 安塞站年降水及年径流系列距平分析成果

2.1 周期性分析

当系列中逐年观测值围绕均值上下分布，并包括丰水段、平水段和枯水段的完整水文周期，且丰枯对称分布时，其代表性好，否则代表性差。绘制安塞站降水量和径流量时序图和5 a滑动平均曲线见图2、3。降水的分布优于径流绕均值的分布，5 a滑动的降水平均值曲线包含2个完整的水文周期(22 a左右)，径流滑动曲线只包含1个完整水文周期(14 a左右)，故用降水过程分析径流过程的代表性更合理。

绘制降水和径流的模比系数差积曲线见图4、5，1952—2015年降水过程包含2个平水段1975—1979、2010—2012年，4个枯水段1964—1972、1993—2001、2007—2010、2012—2015年，3个丰水段1953—1964、1980—1993、2001—2006年；1981—2015年的径流系列包含1个平水段1981—1987年，2个枯水段1996—2000、2002—2015年，2个丰水段1987—1996、2000—2002年。故延河安塞站降水和径流具有丰水、平水和枯水年组交替出现的周期现象，降水变化周期为22 a左右，径流变化周期为14 a左右，故降水变化周期包含了径流变化周期。由于安塞站降水和径流的一致性较好，从降水长系列选择1985—2006年系列是一个完整的丰、平、枯水周期，系列代表性较好。文献[2]要求实测径流系列长度不小于30 a，由于1985年以前相对丰水，2006年后偏枯，故对防洪为主时系列初步选1981—2011年；对供水为主的工程系列初步选1985—2015年。

2.2 长、短系列统计特征值分析

短系列统计参数值与长系列统计参数值接近，认为短系列对长系列有一定代表性。根据安塞站的资料，取编组起始长度为5 a的径流和降水顺时序逐年累进系列均值和变差系数曲线分析，图4中降水量Cv在1953—1992年趋于稳定，而均值在2000年后趋于稳定；图5中径流量的变差系数在1981—2002年趋于稳定，均值在2006年后趋于稳定。根据降水代表性分析成果，对安塞站的长、短系列均值和变差系数Cv及相对误差分析计算见表2。

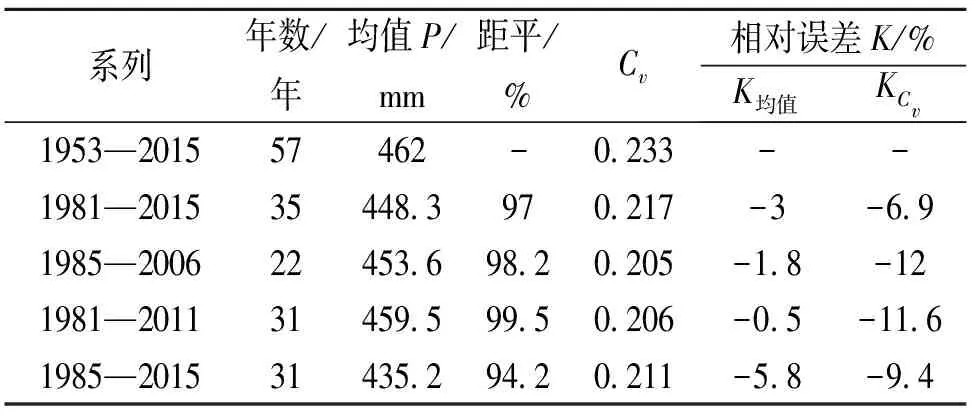
表2 安塞站长短系列统计参数误差统计

注：相对误差K均值=(P短系列-P长系列)/P长系列

从表2可知：1981—2015年降水系列的Cv相对误差最小，比长系列偏小6.9%，1981—2011年系列的均值相对误差最小，比长系列偏小0.5%，1985—2015年系列的均值相对误差最大，比长系列偏小5.8%，径流实测系列1981—2015的均值和Cv值的相对误差均居中。相对误差仅反映长短系列的相似程度，考虑工程的任务和安全富余，防洪工程推荐采用短系列均值与长系列接近的1981—2011年系列，供水工程推荐采用均值和Cv相对误差均居中且包含丰枯组合更多的1981—2015年实测径流系列。

3 结论

延河安塞站径流代表系列短，整体系列偏枯，单一用数理统计法对径流短系列进行分析任意性大，结果不可靠。而降水资料长，丰枯分布对称，具有2个完整的水文周期，利用其与径流一致性较好的关系，通过降水周期性和长短系列统计参数(均值和偏差系数)分析，认为与具有代表性的降水短系列同步的径流系列也具有代表性。延河安塞站1953—2015年降水长系列周期为22 a左右，通过选择不小于30 a的径流长短系列统计参数对比分析，考虑工程的任务和安全富余，防洪工程推荐采用与长系列均值接近的1981—2011年短系列，供水工程推荐采用均值和Cv相对误差均居中的1981—2015年实测径流系列。