群居蜘蛛优化算法在暴雨强度公式参数估计中的运用

2019-01-23苍隋鑫雷冠军

人民珠江 2019年1期

苍隋鑫，雷冠军，梁云，王铁

(1.黑龙江省大庆水文局，黑龙江大庆 163000；2.中国水利水电科学研究院，北京 100038)

水库优化调度、水资源优化配置、水文频率曲线拟合以及水文预报等水文领域相关的研究，都可以归纳为在一定的约束条件下，基于已知的目标函数，寻求目标的最优解。随着计算机运算性能的提高，除了较早的遗传算法[1-2]、粒子群算法[3]，新的智能优化算法如果蝇优化算法[4]、飞蛾火焰优化算法[5]、新型蝙蝠算法[6]及改进粒子群算法[7]等相继被开发应用于水文计算，都在克服早熟收敛和提高运算性能上都取得一定进展。

SSO算法是一种新兴的智能优化算法，通过模拟一种特殊的蜘蛛群体-群居蜘蛛的协作进化行为来构建优化算法。该方法有较好的稳定性和参数估计效果，能够有效避免早熟收敛。SSO算法于2013年首先被Cuevas[8]提出后，由于其良好的寻优特性，在水利科学领域得到了广泛的应用。王文川[9]将其引进单个水库的防洪调度计算中，与传统的动态规划和粒子群优化算法比较，该方法能够有效规避维数灾，计算结果与粒子群算法接近；同时将该方法引入单个水库发电调度中，与动态规划、遗传算法的效能比较，该方法具有较好的寻优效果，具有参数少和搜索效率高的优点，是一种有效的水电站优化调度模型的求解方法[10]。吴光琼、王文川[11-13]分别将其用于水文频率参数估计中，吴光琼[14]将SSO算法用于水位流量关系的拟合，与粒子群算法、遗传算法等方法比较可知SSO算法收敛速度快、全局寻优能力强，能降低水文频率的分析误差，提高理论频率曲线与实测数据的拟合精度。吴光琼[15]运用SSO算法搜索投影寻踪的最佳投影方向，构建SSO-PP模型对水质进行评价，多因子评价结果与单因子结果评价一致，能够使得模型评价结果更加合理可靠。崔东文、Mirjalili[16-17]针对BP神经网络初始网络权值和阈值不易确定的不足，运用SSO算法对BP神经网络的参数的初始值进行估计，采用高维复杂函数对SSO算法验证，并与粒子群算法的性能进行对比，该方法具有较好的寻优能力。Anter[18]运用SSO算法对CT肝脏肿瘤数据集进行分类，用召回率和准确性等对分类结果进行量化表示，结果表明该方法搜索效果好，能够避免局部极小值的出现和具备并行计算的能力。孟昕元[19]运用SSO算法对神经网络控制器参数进行优化，并建立MATLAB/Simulink仿真模型进行验证，表明优化后的神经网络控制器有适应性强、动态过程过渡平稳快捷的优点。

暴雨强度计算公式大都是超定非线性方程，参数估计是暴雨强度公式应用的关键。暴雨强度公式参数估计研究成果大多集中于优化算法的运用和研究。传统的参数估计是采用图解法和LS算法求解参数。遗传算法、免疫进化算法、蚁群算法等[20-22]都被用于暴雨强度公式的参数估计中，取得了较好的参数估计结果。而SSO算法在暴雨强度公式的推求方面未见研究，因而本文将该方法用于暴雨强度公式参数的推求，采用绝对均方误差和相对均方误差为指标与最小二乘法的计算结果进行比较，旨在验证SSO算法用于暴雨强度公式参数估计的可行性。

1 SSO算法简介

SSO算法是对雌雄蜘蛛个体的行为进行数值模拟。该搜索方法能够有效避免早熟收敛，能够在全局范围内进行有效搜索，结果表明该方法的搜索效率高、收敛速度较快。该方法的基本建模原理如下：

a) 蜘蛛个体的初始化，包括雌蜘蛛、雄蜘蛛个体数量、样本以及权重的初始化：

Nf=floor[(0.9-rand·0.25)·N]，Nm=N-Nf

(1)

s(i)=lb+rand·(ub-lb)

(2)

(3)

式中Nf、Nm——雌性、雄性蜘蛛的个体数量，N——样本总数；ub、lb——分量取值的上限、下限；rand——区间[0,1]的随机数；floor——取整函数；J(si)——蜘蛛si个体的适应度值；wi——蜘蛛个体的权重；worsts——最劣适应度值；bests——最优的适应度值。

b) 雌雄蜘蛛个体的相互作用：

(4)

式中Vibci——个体i与个体c之间的信息交流；Vibbi——个体i与个体b的信息交流；Vibfi——个体i与个体f信息交流，个体f是距离个体i最近的雌性个体。

c) 雌雄蜘蛛对外界的振动作出反应。①雌性蜘蛛对外界的反应。判别阈值PF与随机数rm的大小，雌性蜘蛛对外界的反应的数学模拟如下式：

(5)

式中α,β,δ和rand——随机数，k——迭代次数；sc——与个体i距离最小的个体；sb——群体最优值。

②雄性蜘蛛对外界的反应。雄蜘蛛对外界的反应，即蜘蛛个体的进化运动过程，由下式模拟：

(6)

式中wNf+m——排位在中间的雄性蜘蛛；sf——距离雄蜘蛛i最近的雌蜘蛛。

d) 交配生成新个体与新个体进化选择。雌性蜘蛛Sf与排位的雄性蜘蛛Smm在交配半径范围内发生交配行为，对蜘蛛个体的选择依据轮盘赌的方法确定，新生成的蜘蛛与原有的蜘蛛种群进行比较，优势蜘蛛将取代原有的劣势蜘蛛，能够使蜘蛛群体向优势蜘蛛发展。

2 暴雨强度公式推求原理

2.1 基础数据整理

GB 50014—2006《室外排水设计规范》推荐暴雨强度公式的选样方法为年最大值法，要求资料具有20 a以上自记雨量记录。本文收集甘肃某地区1991—2016年共26 a数据，采用10、20、30、45、60、90、120、180 min共8个历时的年最大时段降雨量作为样本值，对该地区的暴雨强度公式进行推求。

2.2 暴雨资料的频率分析

将实测的8个时段的年最大时段降雨量用P-III型分布拟合，计算出理论频率曲线，根据确定的频率曲线，得出降雨强度、降雨历时和重现期的关系，输出推求暴雨强度公式所需的“历时～重现期(即t～P)”数据，见表1，用该组理论值去推求设计暴雨强度公式的参数。

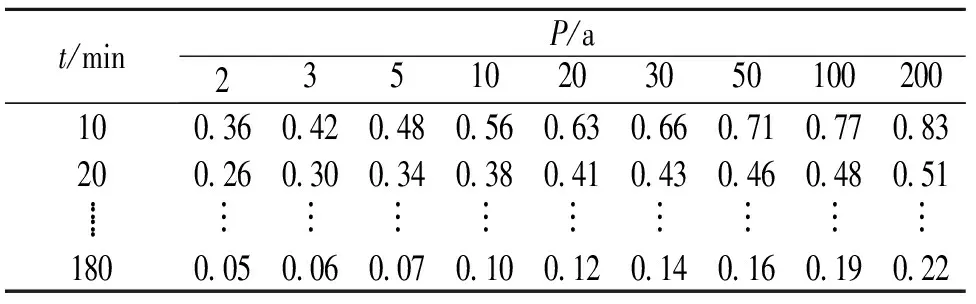
表1 甘肃某地t～P数据 mm/min

2.3 暴雨强度公式参数估计

2.3.1 目标函数的建立

单位时间的平均降雨深度，用i表示，单位以mm/min计；在工程上，暴雨强度常用单位时间内单位面积上的降雨体积q表示,单位以L/(s·hm2)计。q与i之间的换算关系是将每分钟的降雨深度换算成每公顷面积上每秒钟的降雨体积，即：

q=167i

(7)

研究确定暴雨强度总公式：

(8)

式中P——设计暴雨重现期，a；t——降雨历时，min；A1——雨力参数；C——雨力变动参数；b——降雨历时修正系数；n——暴雨衰减指数。

对于暴雨强度总公式，构造目标函数如下：

(9)

式中s——重现期的个数；j——降雨历时的个数。

2.3.2 SSO算法求解暴雨强度公式的步骤

a) 参数序列的初始化。采用式(1)、(2)随机生成A1、C、b、n，为了增大参数的搜索范围，其初始化区间均设为[0,500]，步长取为0.01，用式(9)计算蜘蛛个体的初始适应度值，式(3)计算蜘蛛个体的初始权重值，种群个体设为200，迭代次数设为500次。

b) 参数序列的进化。采用式(4)、(6)进行迭代循环，参数值不断寻优调整，逐步逼近满足目标函数(9)。

c) 循环终止。若循环迭代次数达到最大值或满足迭代终止条件，则停止循环，所得的参数序列即为最优的参数值。

2.3.3 暴雨强度公式精度检验

求出参数A1、C、b、n后，为确保计算结果的准确性，需对暴雨强度计算结果进行精度检验。GB 50014—2006《室外排水设计规范》规定：计算重现期在0.25～10 a时，在一般强度的地方，平均绝对方差不宜大于0.05 mm/min;在较大强度的地方，平均相对方差不宜大于5%。为确保排水工程设计的安全性和经济性，推导公式的暴雨强度应略大于相应的实测暴雨强度，但不宜相差过大，否则经济性欠合理。

将参数A1、C、b、n代入式(7)、(8)中，计算出与t～P数据表相对应的理论暴雨强度值iij，然后根据式(10)、(11)平均绝对方差S总绝、平均相对方差S总相。

(10)

(11)

3 计算结果分析

暴雨强度总公式以各个重现期的总误差最小为目标函数，分别运用LS算法和SSO算法对参数进行估计(表2)，LS算法平均绝对方差为2.32 mm/min，大于规范要求的0.05 mm/min，平均相对方差为713.54%，大于规范要求的5%；SSO算法平均绝对方差为0.02 mm/min，小于规范要求的0.05 mm/min，平均相对方差为7.99%，大于规范要求的5%；LS算法所得结果误差较大，SSO算法所得结果在要求总绝对误差范围之内，结果表明所得的参数结果能够近似计算暴雨强度。

表2 暴雨强度公式参数估计结果

为了进一步检验SSO算法求解暴雨强度公式的计算结果，将重现期是2、3、5、10、20、30、50、100、200 a的判别指标进行计算，见表3。结果表明：除了200年一遇的结果外，不同重现期的平均绝对方差均小于规范要求的0.05 mm/min，表明SSO算法计算的参数估计结果从平均绝对方差方面能够满足规范要求。