图像局部矢量点结构的角点检测算法

唐雪松，谭斌

（西华大学计算机与软件工程学院，成都 610093）

0 引言

在数字图像处理中，图像特征匹配是计算机视觉中一个关键问题，在三维重建、目标识别、目标跟踪等应用中有这重要意义。角点是图像的重要局部特征，在图像中信息含量较高，使用角点进行图像匹配能够减少计算量，因此，角点在图像匹配中被广泛使用。国内外学者对角点有着不同的理解，不同的检测手法形成不同的角点定义，总体上角点检测分为两类：基于图像灰度信息的角点检测算法、基于图像边缘的角点检测算法。

基于灰度信息的角点检测主要通过定义一个CRF函数判断像素点是否是角点。如：Moravec[1]发现边缘像素只有在沿着边缘线的垂直方向有较大的灰度变化，同质区域的像素灰度变化较小，而角点处的每个方向上的灰度变化都比较大。Harris[2]针对Moravec角点中的连续平方求和而引入局部变换因子，利用高斯权重函数特性检测角点进行改进，但是只能很好的检测到L-型角点。Susan[3]采用圆形模板来得到各向同性的响应，不需要计算微分以及非线性响应的特点使得SUSAN算子抑制噪声的性能较好。FAST[4]算法以快速著称，适用于实时性要求较高的图像处理，但FAST算法只能检测单一类型的角点，会出现角点遗漏现象。基于边缘轮廓的方法主要是通过分析图像边缘形状来检测角点。CSS[5]利用Canny边缘检测算子提取图像边缘，并填充边缘轮廓缺口，在大尺度下得到轮廓曲率极大值点，比较T-角点与曲率极大值检测的角点。该算法获得良好的角点检测效果，存在的问题在于如何选择合适的高斯尺度以及角点的阈值。在CSS基础上，He和Yung[6]提出了一种使用自适应曲率阈值和动态支撑区域的检测器。Mohannad和Lu提出了利用弦到点的距离累加算法CPDA[7]，CPDA具有较高的可重复性和较低的定位误差，之后又提出了CPDA的快速算法[8]。但CPDA有一个缺点是估计拐角的曲率值与角度可能不成正比。Freeman链码[9]使用多边形近似方法检查角，并定于两条边的交点为角点。Peng等人[10]在角内侧灰度一致的前提下提出一种可抗背景变化的点对特征，基于点对特征提出一种不受背景影响的角点。

本文在文献[9-10]提出链码和点对特征启发下，提出一种新的角点检测算法。本文从图像边缘着手，提出边缘矢量点结构特征，通过边缘矢量点聚类获取区域内部的链码，在链码的相邻端点处形成角点。

图1 算法流程图

1 矢量点结构特征

图像边缘是图像中的显著特征，是两个区域交接处突出的视觉特征。图像边缘在形态上邻接两个区域，因此，可以对一条边缘进行分解，形成两条边属于各自区域的虚拟边缘。本文模拟这个过程，提出边缘矢量点结构特征。

图2为矢量点特征的示意图，边缘l将图像分为A区域和B区域，点p是边缘l上的点，p1、p2分别为A、B区域在p点邻域的矢量点。

图2 矢量点结构示意图

1.1 矢量点特征提取

为了提取边缘矢量点，先将原始图像做中值滤波，再获取图像梯度，本文使用索贝尔（Sobel）算子与图像做卷积的方式获取梯度。假设待处理图像为A，其沿x方向的一阶梯度为Gx，沿y方向的一阶梯度Gy，梯度幅值G与梯度方向为θ。

图3 Sobel卷积因子

利用式（1）、（2）得到梯度幅值G与梯度方向θ。卷积所得边缘较粗，提取的矢量点过多，存在大量重复的矢量点，为解决这一问题，本文使用非极大值抑制的方式对边缘进行细化。

如图2所示，获取细边缘后，以边缘像素点为始点（p点），沿梯度方向和梯度反方向寻找第一个非边缘像素点（p1点、p2点），以非边缘像素点为终点，终点即为边缘矢量点，矢量点方向为起点指向终点的方向（矢量点p1的方向为p点指向p1点的方向）。

1.2 矢量点特征语义描述

根据边缘矢量点提取方式以及终点像素点自身属性，可对矢量点做如下描述：

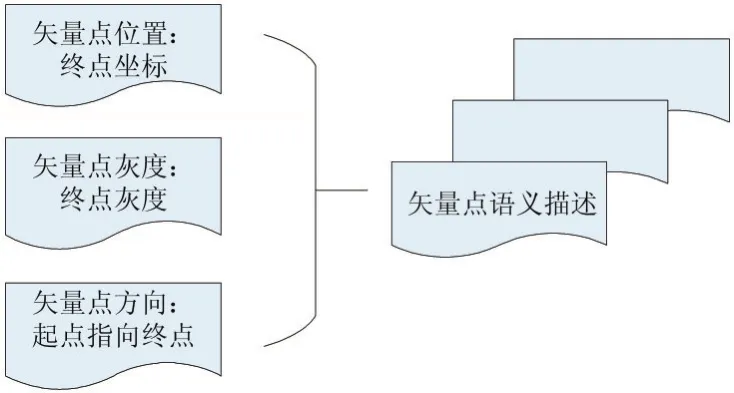
图4 矢量点语义描述

矢量点特征的语义描述是由方向和终点自身属性构成，没有引入其他区域的信息，因此，矢量点特征具有不受外部干扰的特性。

2 角点提取

2.1 矢量链码

矢量点沿边缘分布，且同一边缘相同区域的矢量点具有相似性，同一类的矢量点在形态上类似边缘的链。因此对矢量点进行分类，获取边缘两侧的矢量链码。

图5 矢量点聚类特征线

矢量点特征的语义描述为矢量点分类提供了先前条件。

设第i个矢量点为f(i)，第i个矢量点的x坐标为xi，坐标为yi，邻域阈值T1。第i个矢量点的灰度为g(i)，G[z]为灰度为Z的矢量点。第i个矢量点的方向为d(i)，D(z)为方向为z的矢量点。

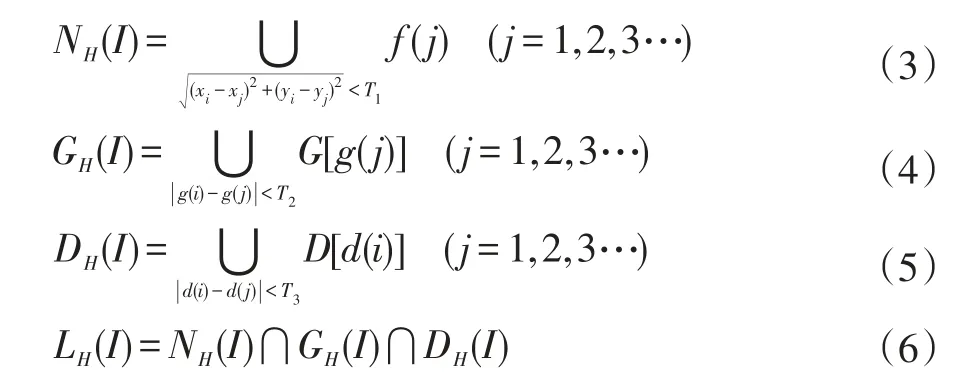
NH(I)：第i个矢量点在邻域阈值T1内的点集。

GH(I)：第i个矢量点在灰度阈值T2内的点集。

DH(I)：第i个矢量点在方向阈值T3内的点集。

LH(I)：以第i个矢量点为端点的特征线。

2.2 链码端点融合获取角点特征

基于图像边缘信息角点提取算法的角点定义为：图像边缘轮廓的交叉点。本文模拟这个过程，以区域内部的链码为轮廓，链码的交叉点即为角点。如图7的C区域，链l1的p1端与链l2的p2端的交点形成角点α1；为避免角点遗失，若相邻链码没有交点，则以链码的相邻端点的中点为角点，如l2的p′1端与l3的p3端形成角点α3。

本文所提取的角点位于角区域内侧，对角点的描述可融合矢量点信息，没有引入角外部背景信息，因此可抵抗背景干扰。

3 实验结果与分析

为证明本文算法的有效性，将本文算法与ORB算法、SIFT算法以及SURF算法做比较，实验图像数据为常用角点提取算法中的图像。

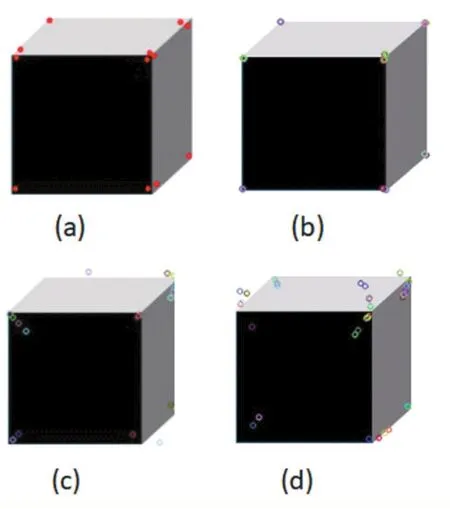
图6 立方体场景下角点提取对比

图 6为立方体场景下本文算法与 ORB、SIFT、SURF提取角点的实验结果对比。本文算法找到了12个角点，分布立方体每个面的角内侧，如图（a）所示。ORB算法找到了37个角点，都位于立方体的顶点处，其中大量角点位置重复，且无法区分这些角点归属于那个面，如图（b）所示。SIFT找到了30个角点，立方体顶部右侧纯在角点遗失现象，且有部分伪角点，如图（c）所示。SURF找到36个特征点，其中部分角点位置重复，且右侧面纯在角点遗失现象。

图7 多种三角形场景下角点提取对比

图7为多组三角形场景下的对比结果。本文算法找到42个角点，分布于三角形角内侧。如图（a）所示。ORB找到了165个角点，钝角三角形的锐角处存在明显的角点遗漏现象，如图（b）所示。SIFT找到了109个角点，伪角点较多，如图（c）所示。SURF找到100个角点，也纯在伪角点。

由两组对比实验可看出，本文算法检测提取的角点无论在数量上，还是在定位上都优于其他三种角点检测算法。

4 结语

传统的基于边缘的角点检测器主要依赖于图像边缘的几何信息提取角点，而基于灰度变化的角点检测器主要依赖于图像的灰度变化。本文算法将两者结合，提出角区域内部的角点，融合了边缘信息与角内侧区域信息，使得角点提取与描述更加准确。从仿真实验结果可以看到，本文提出的角点检测算法能够较好地检测到真实角点，避免对角点的漏检与误检，提高了角点检测器的检测性能。

对本文后续研究的讨论：①矢量点提取基于边缘像素，对于复杂或大尺度的图像所提取的矢量点过多，矢量点聚类属于层次聚类范畴，消耗时间过多，在实时性上不足，今后工作将对算法进行优化。②角点位于角区域内部屏蔽了背景信息，可抵抗背景干扰，对图像匹配由着重要的作用。未来的工作也将尝试把本文算法应用于图像匹配方面。