数学规划法在有限元模型修正中的应用

张 欣，于 澜，张 淼

(1.长春工程学院电气与信息工程学院，长春 130012；2.长春工程学院理学院，长春 130012)

0 引言

有限元模型修正是20世纪90年代以来模态分析与试验所面临的一大挑战。工程和科学系统的现代分析中，人们已经投入了大量的努力用于修正被曲解的计算机模型。这种模型修正的主要目的是预测系统对干扰的响应和预测从修正后系统中所获得的可能的设计优势。从当前的实践来看，这一目的可以通过修正系统的外形结构来获得。在实践中已经能够从离散模型中产生数值的预测，但当预测结果与实验结果相比较时，人们发现没有自信把这个模型用于实际中，因为预测结果与实验结果的相关度并不理想。

为了解释在预测和观察之间的相关度缺乏问题，有必要考虑导致解析模型不精确的几种可能的原因。除了实验测量过程会产生误差，还有3个一般会遇到的模型误差的存在形式，它们也可能会引起模型预测的不准确性：1)模型结构误差：在建模过程中发生在控制物理方程有不确定性的时候，或者在工程系统具有强非线性行为的时候；2)模型参数误差：它通常包含于应用了不适当的边界条件和为了简化模型所采用的不精确的假定的过程；3)模型阶数误差：它来自于复杂系统的离散化，它会导致产生了一个阶数不足的模型，尤其重要的是模型阶数可以被认为是模型结构的一部分[1]。

利用实测的结构模态信息来修正结构的有限元解析模型，使修正后的有限元模型的输出信息与实测信息最大程度相符合，这就是有限元模型修正。修正后的有限元模型能够更好地反映结构的动力特性[2]。目前，较为常见的有限元模型修正方法有矩阵元素型、灵敏度矩阵方程型和残差型3种。矩阵元素型的模型修正方法的基本思路是：首先假定原始的有限元模型与真实结构模型之间只存在微小差异，然后，除了保持刚度矩阵和质量矩阵的对称性、正定性和稀疏性以及振型正交性等性质外，还要在满足特征方程的条件下，利用最小二乘法求出符合实测结果的刚度和质量矩阵[3]。灵敏度矩阵方程型的模型修正方法是为了使测量模态模型与分析模态模型之间的相关性达到最大化。这些方法可以广泛地选择修正参数，一般来说，这些方法都是基于模态数据的截断泰勒级数展开作未知参数的函数建立灵敏度矩阵方程δz=Sδθ，其中δθ是参数扰动，δz是测量输出的扰动，S是灵敏度矩阵。不同组的修正参数可能会使识别问题成为病态的或数值不稳定的。残差型模型修正方法是构造含有解析的修正参数的函数与它的实测数据之间的残差向量，利用各种寻优算法，取得残差为0时的设计参数的最优解，其中修正参数关于设计参数的函数关系的显化及优化问题的求解是其主要难题。灵敏度矩阵方程型及残差型模型修正的结果具有明确的物理意义，便于实际结构的分析与计算，并与其他优化设计过程兼容，实用性强。本文将对基于残差法建立数学模型的模型修正方法进行研究。

1 实模态参数与复模态参数[4-5]

描述自由度为N的线性阻尼离散系统的自由振动方程为

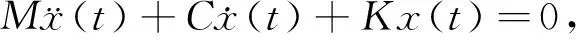
(1)

相应地其强迫振动方程为

(2)

式中M，C和K分别为系统的质量、阻尼和刚度矩阵。令C=0，则无阻尼固有频率与实模态对(λi，vi)(i=1，2，…，N，λ=w2=-ω2)满足方程

(K+λiM)vi=0。

(3)

可以计算得到实频率λ1，λ2，…，λN及实模态v1，v2，…，vN。常用的规范正交化条件为

VTMV=E，VTKV=diag(-λ1，…，-λN)，

(4)

其中V=[v1，…，vN]。实频率及实模态，有时也包括阻尼比，统称为实模态参数。

考虑阻尼时的系统复频率及复模态对(si，ui)(i=1，2，…，2N)满足方程

(5)

它们的规范正交条件的形式有很多[6]，常用的形式为

ΦTAΦ=E，ΦTBΦ=diag(-s1，…，-s2N)，

(6)

其中Φ=[φ1，φ2，…，φ2N]，φi=[uiλiui]T(i=1，2，…，2N)，且

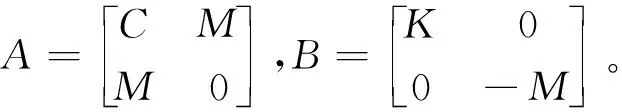
(7)

下文讨论中用到的均为经过式(4)和式(6)规范正交化后的实模态和复模态。

2 定义残差法的目标函数

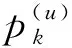
minΔR=f(p)-f(p(o))，

(8)

寻找p的最优解p*。

式(8)是一个无约束非线性优化模型，从数学角度来说，它有众多解法，人们除了使用最速下降法外，还使用并发展了Newton法及其改进算法，例如阻尼Newton法，带保护措施的阻尼Newton法，吉尔·默里稳定Newton法等。尽管收敛速度较慢，但最速下降法最优质的特点是结构简单且计算代价较小；相较而言，Newton法及其改进Newton法收敛速度较快，尽管在每一步迭代时，都需计算目标函数的二阶导数来构成海森矩阵，确定搜索方向，然后再求解一个线性方程组，计算工作量大，从而抵消了Newton法收敛速度快的优点。

由Daviden发明的变尺度法即拟Newton法，是无约束优化计算方法中最杰出的、最富有创造性的工作。不同于Newton法，拟Newton法在构造搜索方向时避免了计算海森矩阵，减少了计算量，且具有超线性收敛速度。Broyden、Powell和Fletcher等人沿着这一方向做了大量的工作，提出了PSB公式、BFGS公式以及DFP公式等一组著名的校正公式，形成了Broyden族拟Newton法。1970年Huang提出了一类比Broyden族拟Newton法更为广泛的校正公式，即Huang族拟Newton法，它取消了Broyden族对修正矩阵的对称性限制。Powell直接方法和共轭梯度法在无约束最优化计算方法中也占有十分重要的地位，由于Broyden族拟Newton法对于中小规模的无约束优化问题，是一类非常有效的方法，但在求解过程中，它要存储一个n×n阶矩阵，这对大规模无约束问题来说，会因为计算机内存的限制而无法使用。再则，它需要不停地求解线性方程组，因此，算法的效率受到了影响。高效且需较少存储量的求解大规模无约束最优化算法，即为共轭梯度法。例如，对正定二次函数的共轭梯度法有Polak-Ribiere-Rolyak共轭梯度法、Fletcher-Reeves共轭梯度法、Dixon共轭梯度法和Crowder-Wolfe共轭梯度法等。对于正定二次函数来说，如果以上几种共轭梯度法均采用精确线性搜索，则它们是等价的。但在实际中，最常用的是FR方法和PR方法。由于FR方法中的βk计算最简单，因此应用得最多。而对于非二次函数的共轭梯度法，将共轭方向法应用于非二次函数的极小化，每迭代n次就周期地取负梯度方向作为搜索方向，称这种算法为重新开始的共轭梯度法。Beale-Powell提出在当前点重新开始时，以算法产生的方向作为重新开始的搜索方向，即要求新一轮的搜索方向对二次函数仍是共轭方向，即Beale-Powell三次重新开始共轭梯度法。

在一些无约束最优化问题中，由于目标函数的特殊性，它的海森矩阵G(x)是稀疏矩阵，若用通常的拟牛顿法求解这类问题，所构造的用于逼近海森矩阵的矩阵Bk不具有与G(x)相同的稀疏结构，因此，形成了一般稀疏拟牛顿法和基于BFGS校正公式的稀疏拟牛顿法。到目前为止，拟牛顿法中的BFGS算法是最有效的求解无约束优化问题的方法。将其改进，减少其存储量，使之能适用于求解大规模无约束最优化问题，即为无记忆拟牛顿法，它在计算过程中不需要存储矩阵Bk，具有内存小、收敛速度快的特点，特别适用于求解大规模无约束优化问题。

但在实际问题中，由于具体建模所采用的修正参数不同，模型也不同，所选择采用的算法也可能更加适用和灵活。

2.1 频率残差

模型修正的目的就是以t个修正对象的实测数据作为支撑来优化得到设计参数的最优值作为修正值。接下来，依据不同的修正参数，建立下列几种残差型的优化模型。

将模型修正的目标函数[8-9]定义为

(9)

式中：p1、p2为设计参数的上下限值；t为实测数据的个数，

D(p)=(D1(p)D2(p) …Dt(p))T

为t个频率的残差向量，其中

Di(p)=λi(p)-λi(p(o))。

将模型修正的目标函数[2，10-12]定义为

(10)

式中：p1、p2为设计参数的上下限值；t为实测数据的个数。

Df(p)=(D1(p)D2(p) …Dt(p))

为t个频率的残差向量，其中

式中：λi(p)为第i阶无阻尼固有频率关于设计参数的显式函数关系；λi(p(o))为第i阶无阻尼固有频率的实测数据值。

将模型修正的目标函数[13]定义为

(11)

式中：W为权矩阵；p1、p2为设计参数的上下限值。

2.2 模态残差

将模型修正的目标函数[14]定义为

(12)

式中：W为权矩阵；p1、p2为设计参数的上下限值。

为t个频率的残差向量，且

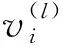
将模型修正的目标函数[15-16]定义为模态MAC值的残差形式：

(13)

其中

式中：vi(p)为有限元模型第i阶模态振型关于设计参数的显式函数关系；vi(p(o))为第i阶模态振型的实测数据值。

有时模态残差也定义为如下形式：

(14)

但这种形式应用得还不够广泛。

2.3 频率和模态的综合残差

将模型修正的目标函数[17-21]定义为频率残差与模态残差的加权综合式：

minf(p)=Df(p)WfDf(p)+r(p)TWmr(p)，

(15)

式中Wf、Wm为频率残差和模态残差的权矩阵。

还可以将模型修正的目标函数[22-23]定义为频率残差与模态残差如式(16)的加权综合式

(16)

式中W为权矩阵。

2.4 方程残差

将模型修正的目标函数定义为实测频率数据和实测模态数据同时满足特征方程，来获得特征方程中的刚度或质量矩阵的修正量。以刚度阵的修正为例，假设修正后的模型的刚度矩阵可以用初始模型中的各单元的刚度阵线性表示，即

式中：αi为第i个单元的刚度矩阵的修正系数；Koi为原始模型中第i个单元的刚度矩阵；Ne为结构模型的单元数。目标函数[24]定义为

(17)

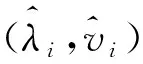
3 对残差法目标函数的寻优策略

在上文建立的10个优化模型中，除了式(13)～(17)是无约束非线性规划外，式(8)～(12)均为约束非线性规划模型。针对约束优化模型，求解约束最优化问题的方法大致可分为3类：

第1类是将约束问题转化为一系列无约束问题求解，用这一系列无约束问题的极小点去逼近原约束问题的最优解——序列无约束极小化方法(Sequnential Unconstrained Minimization Techniqe)，简称SUMT方法，有代表性的是惩罚函数法(penalty function method)和广义拉格朗日乘子法(Generalized Lagrange Multiplier Method)。这种方法主要是各种不同形式、不同特性的罚函数法，依赖于如何将目标函数与约束函数进行组合，导出不同形式的罚函数。只要恰当地实施，这类方法，就可拥有较好的收敛速度与数值稳定性，一直是求解约束优化问题的主要方法。

第2类是在每个迭代点处构造一个二次函数去逼近目标函数，用线性函数逼近约束函数。将对原约束问题的求解转化为对一系列二次规划子问题的求解，以子问题的解作为本次迭代的搜索方向，沿搜索方向寻优得到新迭代点，迭代序列最终逼近原约束问题的最优解——序列二次规划法(Sequential Quadratic Programming，常简记为SQP)方法。各种方法差异主要在于构造二次函数的海森矩阵的方法不同。特别地，若以变尺度法(拟Newton法)构造海森阵，形成二次规划子问题——约束变尺度法，代表性方法为WHP (abbr.water horsepower)方法。后经不断改进，SQP类方法已成为用于求解非线性约束最优化问题最有效的算法，它不仅可以求解带有等式约束的优化问题，而且可以很容易地处理不等式约束，这类算法不仅可以具有全局收敛性，而且具有局部超线性收敛或更强的二次收敛性。

第3类是处理线性约束问题的方法在非线性约束时的推广，如广义消去法、可行方向法、广义简约梯度法和投影梯度法等。这些方法所产生的迭代点均是约束优化问题的可行点。但由于约束函数的非线性属性，这些方法的实施要比处理线性约束问题时所使用的相应算法复杂得多，因此，算法的效果不算理想。代表性的是可行方向法(feasible direction method)，它是一种直接处理约束的方法。它的特点是在迭代过程中目标函数要求沿着可行下降方向寻优，主要的方法是佐登第克(Zoutendijk)可行方向法、托克斯—凡努特(Topkis-Veinotl)可行方向法、投影(projection)梯度法、简约梯度法等。

但在模型修正的应用过程中，远没有达到能广泛使用约束优化方法的程度，下面仅介绍在模型修正过程中建立残差型目标函数后的常用的优化算法。

3.1 稳定性条件方程求解

用稳定性条件

(18)

求解式(17)，然后得到稳定点，认为是最优点。显然式(18)的求解变成一个超定或欠定方程组的求解，引入广义逆技术求解[24]。

3.2 优化算法求解

在不考虑约束条件，直接用共轭梯度法中的PR算法，求解形如式(9)的无约束优化模型[8]，或自适应模拟退火优化算法求解[11]。对形如式(10)的非线性约束优化问题，采用有限元分析软件ANSYS先后用两种优化方法：零阶和一阶方法求解[2]，或用序列二次规划法(SQP)求解[10]。对形如式(11)的优化问题采用混合优化算法求解[13]。对形如式(12)的约束优化问题，采用罚函数法化为无约束优化问题，对该无约束问题用最速下降法求解[14]。对形如式(13)的优化问题，可以采用遗传算法求解[16]。对于形如式(15)和式(16)的优化问题，通常采用的优化算法是基于灵敏度的迭代程序，在信赖域内优化目标函数，利用目标函数f(p)的泰勒级数截断形式可以定义一个二次型

z(p)=f(p)+2f(p)]Δp。

Δp在迭代算法中代表一个步长向量，f(p)与[2f(p)]是f(p)的梯度与海森矩阵，经过某次迭代过程，使f(p)≈0，从而得到近似的最优值p*。在每次迭代中，优化算法都在当前点附近，构建一个模型函数z(p)，并确定一个围绕当前点的信赖域，优化值p*可以在信赖域中获得，在每步迭代中搜索步长都限定在信赖域内，避免了过大步长的出现。目前常用的算法有信赖域牛顿算法[19，21]或高斯牛顿算法[17]等。

4 结语

我们实际模型修正问题中遇到的目标函数，常常利用非线性最小二乘法来建立残差型优化模型。对待非线性最小二乘问题，若采用牛顿类算法，则在迭代点取目标函数的二次近似式的最优解作为搜索方向或修正向量。由于是对残差在平方和意义下取极小，极有可能残差在最优解处的值为零(零残量问题)，或较小的值(小残量问题)海森矩阵G(x)中的非线性项为0，或者相对线性项来说较小，因此，在最优值的某个邻域内G(x)的线性项作为海森矩阵G(x)的一个很好的近似，即为著名的高斯—牛顿法。如果δ(k)为f(x)在点x(k)处的一个下降方向，取d(k)=δ(k)为搜索方向进行线性搜索，并令x(k+1)=x(k)+αkd(k)即为阻尼高斯—牛顿法，其中αk为由线性搜索确定的步长。

布朗与丹尼斯(Brown，Dennis，1971)，贝茨(Betts，1976)，丹尼斯，盖伊和韦尔舒(Dennis，Gay and Welsch，1981)以及吉尔—默里(Gill-Murray，1978)等提出用拟牛顿修正产生对海森矩阵G(x)中的非线性项的近似。上述几种产生矩阵Ck去形成海森矩阵G(x)的近似矩阵Bk的方法，在实际计算时，有时效果不如预期的好。原因在于Ck的近似程序不够理想，且随着迭代过程的进行，误差会越来越大。克服这一困难的一个可取办法是采用调比技术，即在对矩阵Ck作修正之前，先选择一个调比因子来建立修正公式。混合算法(又称杂交算法)是一类以高斯—牛顿法为基础的算法。混合算法把高斯—牛顿法同一般的无约束最优化方法进行组合，并能在求解问题的过程中自动地调节到适合问题特性的方法，因而也称为开关算法。分解式拟牛顿法是另一类即利用非线性最小二乘问题的特点，又利用拟牛顿修正产生目标函数海森矩阵近似的方法。以上非线性最小二乘法在模型修正中的应用还不普遍，但它却是最适合残差型模型修正的算法之一。

另外，可行内点弧算法(feasible arc interior point algorithm)[25]对非线性不等式和等式约束的优化问题来说，是一种新的技术。它需要在不等约束的内点中得到一个初始点，然后产生一系列的内点。当问题仅仅是含有不等约束，我们的模型用连接变量和等式约束来引入多学科带来的影响，就像在典型的优化模型中，状态方程能得到隐式处理，从另一方面说，在同步分析和设计优化问题中，状态方程可以看成是那些规划的一部分。可行内点弧算法减少了状态方程所给出的等式约束中的状态变量，最新颖的一点是这种减少是通过不需要解状态方程来完成的，它阐述了解以线性化平衡方程给出的等式的系统解法，而且它能有效地应用在解决工程问题的规范的解算器上。